早期数学笔记,大量使用chatGPT辅助,当时不会Tex,直接放图;中英混杂,但是集合基础部分,不再进行整理。
- Basic knowledge
- Definition
- A⊕A= ∅
- A⊕∅=A
- Cantor’s paradox
- Russell’s paradox (罗素悖论)(Russell’s antinomy)
- power set
- Cardinality
- Cartesian Product
- Let A,B,C be sets. Is A ×(B ×C)=(A×B)×C?
- Formal Languages: symbols
- Set Operations for languages
- Set Equality
- Laws of Set Operations
- Derived Laws
- Two Useful Results
Basic knowledge
formal reasoning (logic):形式推理、逻辑推理
A set is a collection of objects (elements). If x is an element of A we write x ∈ A
Elements are taken from a universe, U,– but this can be quite complex, e.g. numbers, and sets of numbers, and sets of sets of numbers, etc.
Not all “well-defined” universes are possible, e.g. No “set of all sets” (Cantor’s paradox) No “sets which do not contain themselves” (Russell’s paradox)
multiplicity:多重性
A set is defined by the collection of its elements. Order and multiplicity of elements is not considered.
We distinguish between an element and the set comprising this single element. Thus always a!= {a}.
Set ∅ = {} is empty (no elements);
Set { { } } is nonempty — it has one element
Definition
For sets S and T, we say S is a subset of T, written S ⊆ T, if every element of S is an element of T
Take Notice:
S ⊆T includes the case of S = T S ⊂T —aproper subset: S ⊆ T and S=T ∅ ⊆S for all sets S S ⊆U for all sets S N>0 ⊂N⊂Z⊂Q⊂R An element of a set; and a subset of that set are two different concepts:
a ∈{a,b}, a ̸⊆ {a,b}; {a} ⊆ {a,b}, {a} /∈ {a,b}
Take notice of such nested empty sets! they are different entity! interval notation

区间符号:interval notation
Constructions from other, already defined, sets
Union (∪), intersection (∩), complement (·c), set difference (), symmetric difference (⊕)
Power set Pow(X) = { A:A ⊆ X }
Cartesian product (×)
A∪B–union (a or b):
A∪B ={x :x ∈A or x ∈B}.
A∩B–intersection (a and b):
A∩B ={x :x ∈A and x ∈B}.
$A^c$ – complement (with respect to a universal set U):
$A^c$ ={x : x ∈U and x /∈ A}.
We say that A,B are disjoint if A ∩B = ∅
A\B =A∩$B^c$
symmetric difference (xor)
A⊕B =(A\B)∪(B\A)
A⊕A= ∅
A⊕∅=A
Cantor’s paradox
Proof: Assume the contrary, and let C be the largest cardinal number. Then (in the von Neumann formulation of cardinality) C is a set and therefore has a power set 2C which, by Cantor’s theorem, has cardinality strictly larger than C. Demonstrating a cardinality (namely that of 2C) larger than C, which was assumed to be the greatest cardinal number, falsifies the definition of C. This contradiction establishes that such a cardinal cannot exist.
Russell’s paradox (罗素悖论)(Russell’s antinomy)
It is a little hard to understand, Russell set wanted to contain any sets that are not belong to itself, but which leaded to the antinomy.
For better comprehension, we can use the analogies, such as The barber with “shave”(It is a antinomy)
According to the unrestricted comprehension principle, for any sufficiently well-defined property, there is the set of all and only the objects that have that property. Let R be the set of all sets that are not members of themselves. (This set is sometimes called “the Russell set”.) If R is not a member of itself, then its definition entails that it is a member of itself; yet, if it is a member of itself, then it is not a member of itself, since it is the set of all sets that are not members of themselves. The resulting contradiction is Russell’s paradox. In symbols:

power set
所有子集的集合
The power set of a set X, Pow(X), is the set of all subsets of X
Pow({a,b}) = { ∅,{a},{b},{a,b} }
Cardinality
The cardinality of a set X (various notation) is the number of elements in that set.
|X| = #(X) = card(X)
Always |Pow(X)| = $2^{|X|}$
(仅适用于非单一∅集合,也适用于{∅},但是不适用于只有一个∅元素)
我再重新解释下我自己领悟的这句话,∅比较特殊,他的子集就是自己
(∅是任何集合子集,但是没有元素),但是没有基数元素,单独考虑
但是如果论{∅}或{a, ∅},则这不是空集,这是一个非空集合,有一个空集元素,适用 |pow({∅})|=2^1
如果有{}(即∅)作为元素,则基数是 |2^n – 1|
|∅| ? =0
Pow(∅) ? = {∅}
|Pow(∅)| ? =1
Pow(Pow(∅)) ? = pow({∅})={{∅}, ∅}
|Pow(Pow(∅))| ? =2
|{a}| ? =1
Pow({a}) ? ={∅, a}
|Pow({a})| ? =2
|[m, n]| ? =
Pow({a,b,∅})={∅,{a},{b},{∅},{a,b},{a,∅},{b,∅},{a,b,∅\}\}
So | Pow({a,b,∅})| = 2^3 = 8
Relatethecardinalities to |A∩B|, |A|, |B|
|A∪B| = ∣A∣+∣B∣−∣A∩B∣
|A \ B| = ∣A∖B∣=∣A∣−∣A∩B∣
|A⊕B| = ∣A∣+∣B∣−2∣A∩B∣
Cartesian Product
Notice, the cross product is orderd pairs
(a,b) is different from (b,a)
It is similar to points, they are both ordered pairs, (a,b) is different from (b,a)

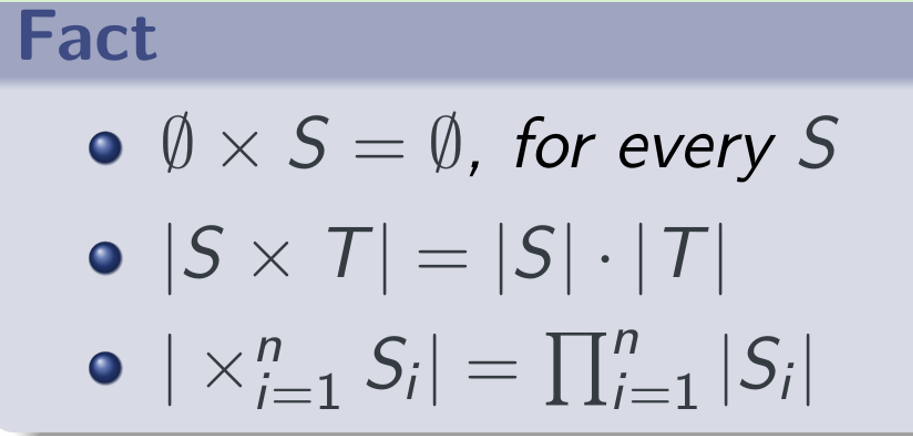
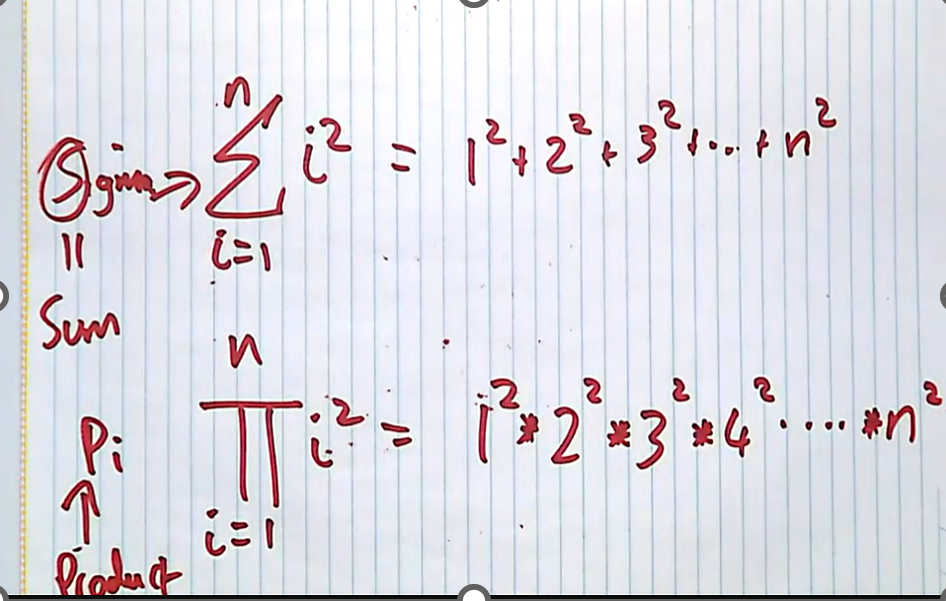
Let A,B,C be sets. Is A ×(B ×C)=(A×B)×C?
Of course Not.
A ×(B ×C)=(a, (b, c))
(A×B)×C=((a, b), c)
Formal Languages: symbols
Σ —alphabet, a finite, nonempty set
Examples:
Σ={a,b,…,z} for single words (in lower case)
Σ={0,1} for binary integers
Σ={0,1,…,9} for decimal integers
A word is a finite string (sequence) of symbols from Σ.
The empty word, λ, is the unique word with no symbols
Examples
w =aba, w =01101…1, etc.
length(w) — # of symbols in w
length(w) = 3,length(λ) = 0
The only operation on words (discussed here) is concatenation, written as juxtaposition
vw,wv,wvw,vwv,…
Take Notice
λw =w =wλ
length(vw) = length(v) + length(w)
Examples
Let w =abb, v = ab, u = ba
vw =ababb
ww =abbabb = vubb
wλv =abbab
length(vw) = length(ababb) = 5
Formal Languages: Sets of words


For example, the Math language conceived :

HTML language:
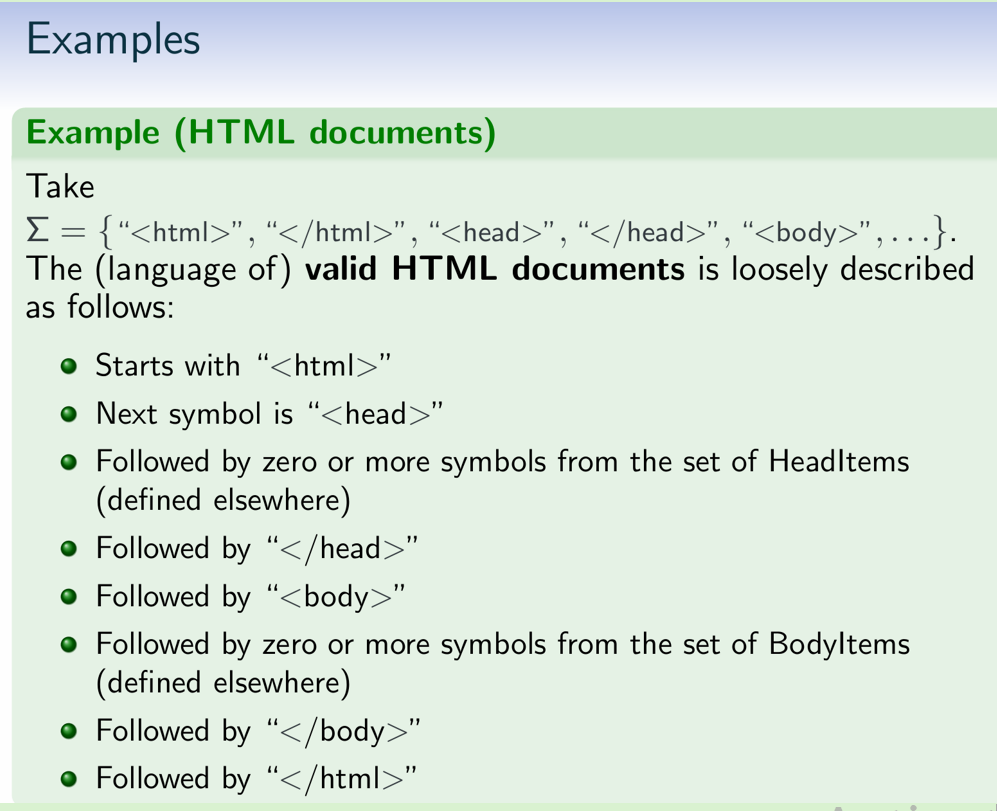


Set Operations for languages

这是说语言的操作
$\Sigma^*$ 是所有语言的父集合,因为拥有“all finite words”
语言是其子集
X的*次方,是X自己叉乘自己几次


Set Equality
Venn diagrams can help visualize, but are not rigorous.
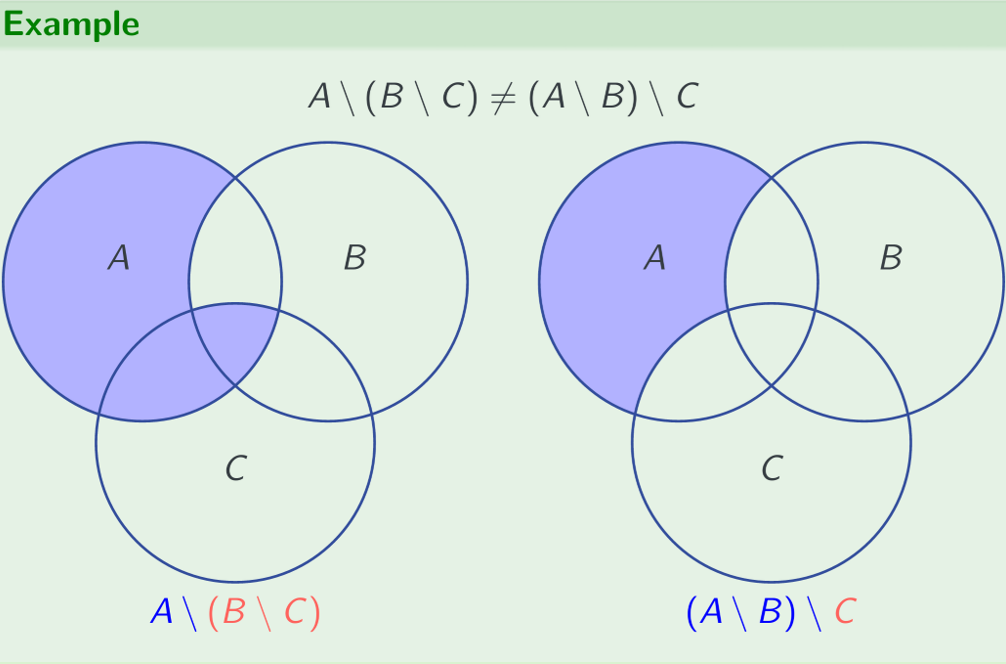
(0, 4) = {1,2,3} = {3,2,1}
Laws of Set Operations

Derived Laws


Two Useful Results






Welcome to point out the mistakes and faults!