Recently I struggle with math, Paul taught 3 lectures in 26th and 27th September, with plenty of concepts and notions. I didnot got much during the lessons, there was a big mass among those wonderful concepts in my brain. It has been nearly 2 weeks after that, I spent 4 days watching the recordings and sorted out those concepts with my annotations about my confusions during the first learning.
It is a little different from algebra and geomatry. I suggest to know the definitions, and then just try to infer or understand those inferences.
Relation Definition and Examples
An n-ary relation is a subset of the Cartesian product of n sets.
To show tuples related by R we write:
$(x_1,x_2,\dots,x_n)\in R$ or $R(x_1,x_2,\dots,x_n)$
If n = 2 we have a binary relation R ⊆ S×T and to show pairs related by R we write:
is the domain of R, and we say R is a relation on U (or on S if $S_1= \dots =S_n=S$ and n is clear).
Remeber these definition, later we may use ‘<’, ‘>’ or ‘=’ to replace ‘R’ (namely relation) literally as an expression.
Example: These are relations
Equality: $=$
Inequality: $≤, ≥, <, >, \neq$
Divides relation: $|$
Element of: $∈$
Subset, superset: $⊆, ⊂, ⊇, ⊃$
Congruence modulo n: $m\underset{(n)}{=}p$
Example: a binary relation
S =set of CSE students (S can be a subset of the set of all students)
C =set of CSE courses (likewise)
E =enrolments = { (s,c):s takes c }
hence
In practice, almost always there are various ‘onto’ (nonemptiness) and (uniqueness) constraints on database relations.
Note, here mentioned nonemptiness and uniqueness, if you operated a database, such as mysql, you would easily understand why to set part of columns unique or nonempty.
Uniqueness means that there must be one column with unique values in database; Nonemptiness means that in $S_1 \times S_2 \times S_3$, there are must 3 elements in the three sets.
Example: 3-ary relation
Example (Class schedule)
C = CSE courses
T = starting time (hour & day)
R = lecture rooms
$\therefore$ S = schedule = { (c,t,r) : c is at t in r } ⊆ C×T×R
Binary Relations
A binary relation between S and T is a subset of S×T: i.e. a set of ordered pairs.
Also: over S and T; from S to T; on S (if S = T).
Note on S, it means the relation is on S itself, namely $S \times S$.
Special (Trivial) Relations
Identity: (diagonal, equality) I = {(x,x):x ∈ S }
Empty: ∅
Universal: U = S×S
Defining binary relations: Set-based definitions
Defining a relation R⊆S×T:
Explicitly listing tuples: e.g. {(1,1),(2,3),(3,2)}
Set comprehension: {(x,y) ∈ [1,3] × [1,3] : 5|xy − 1}
Construction from other relations: {(1, 1)} ∪ {(2,3)} ∪ {(2,3)}← (note that ←)
Matrix representation

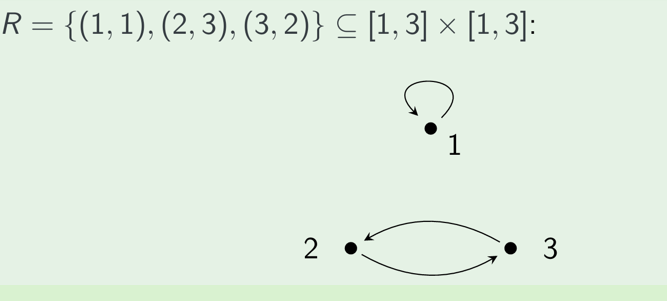
graphical representation
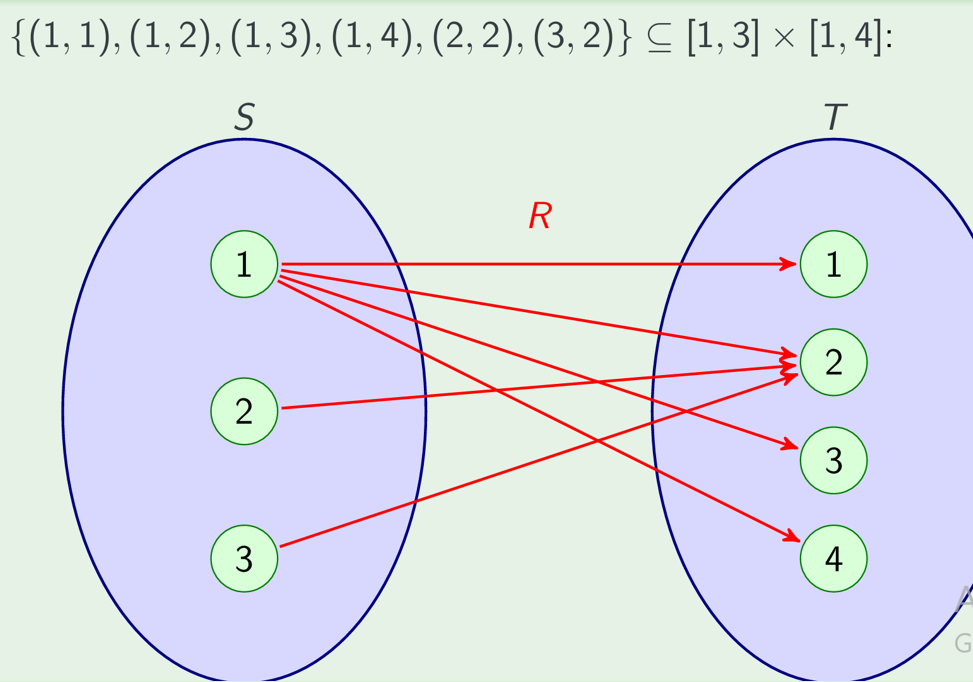
Or as a directed graph, R = S×S , Nodes are emelents(domain, namely S), edges are elements of R(relation)
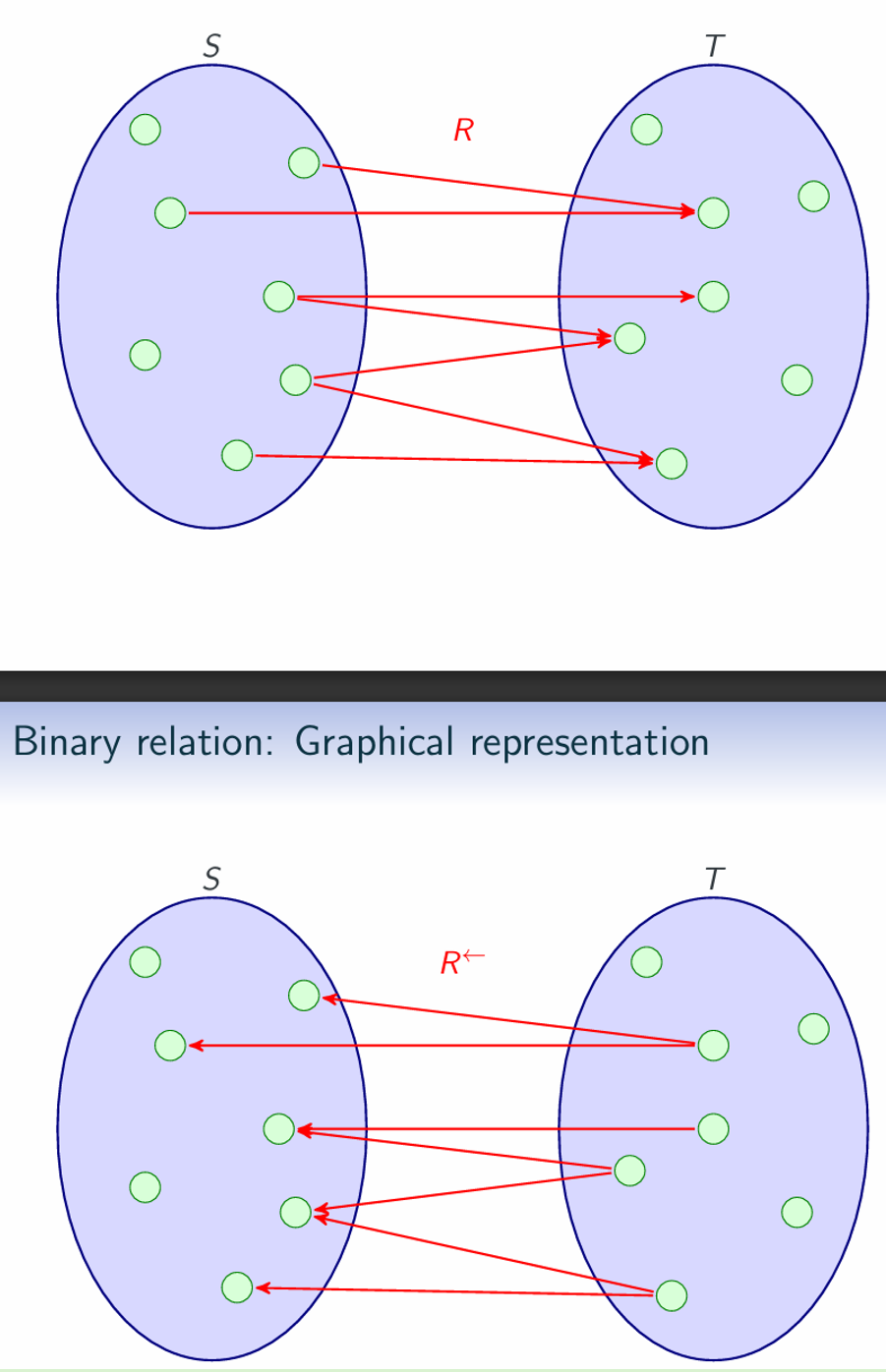
Operations for binary relations: Converse and Composition
Relations are sets, so the standard set operations (∩, ∪, , ⊕, etc) can be used to build new relations.
Two operations that apply to binary relations uniquely:
Converse: If R⊆S×T is a relation, then $R ^ \leftarrow \subseteq T \times S$:
Composition: If R1⊆S×T and R2⊆T×U then R1;R2 ⊆ S×U:
Fact:
Graphical representation
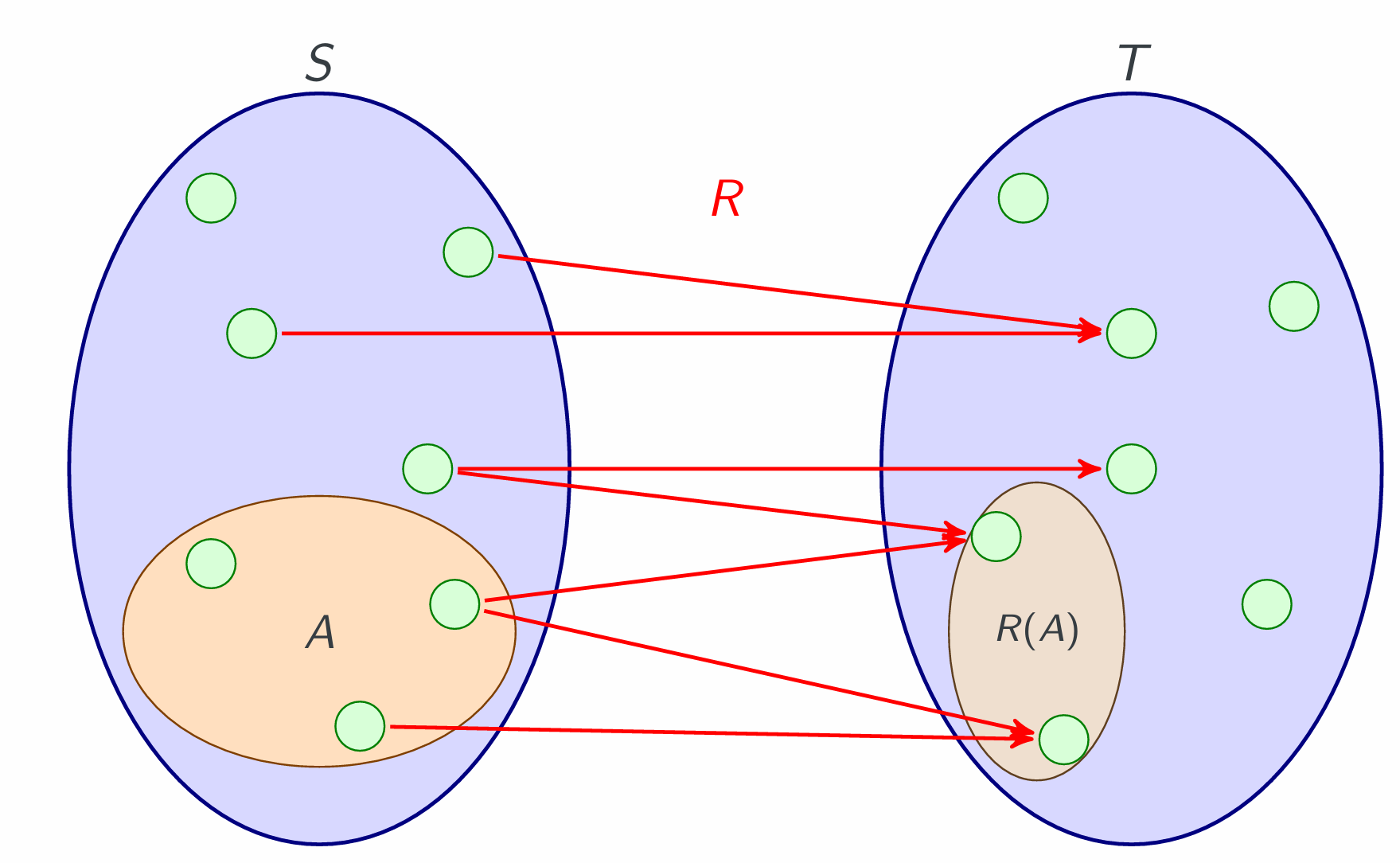
Relational image definition
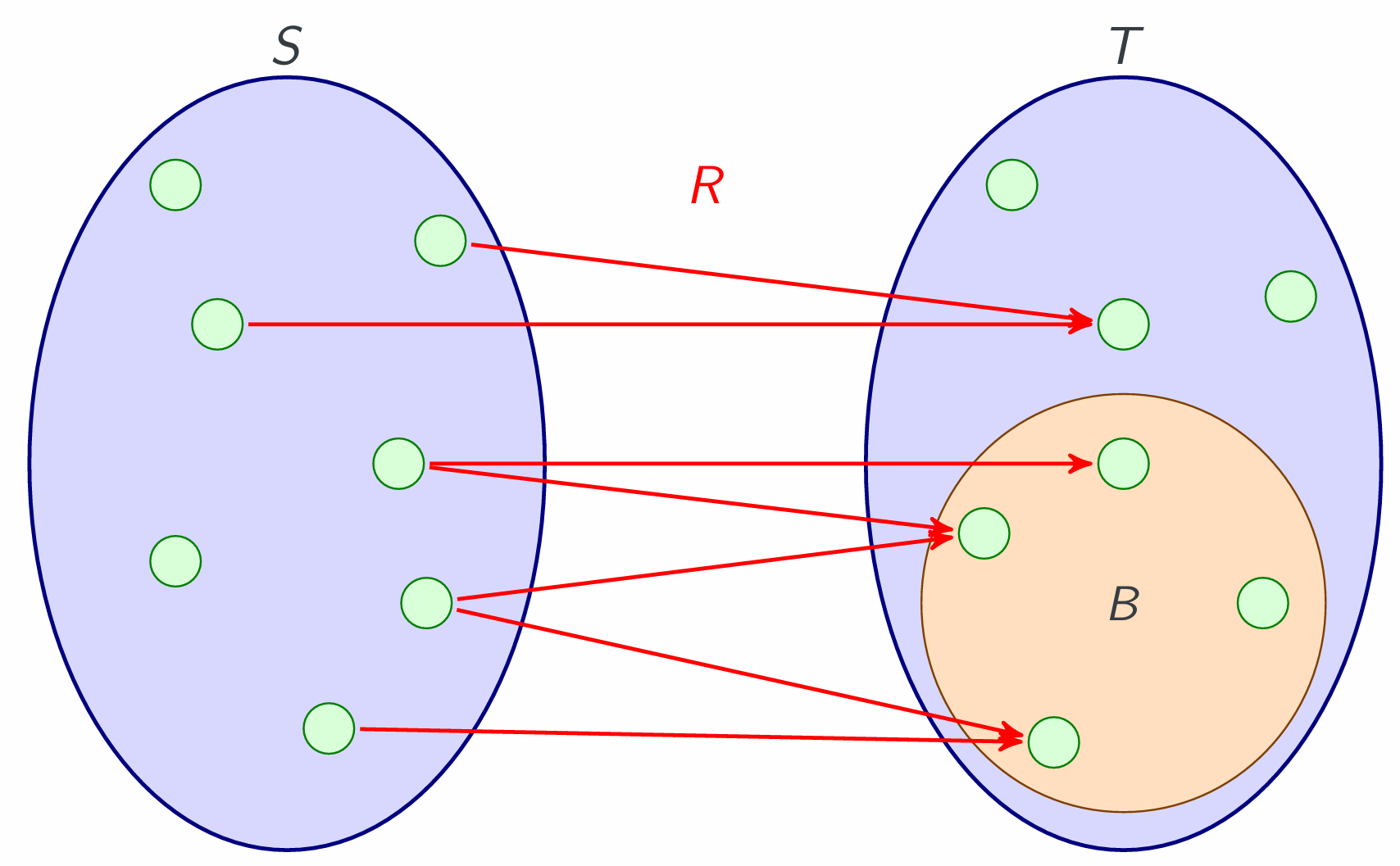
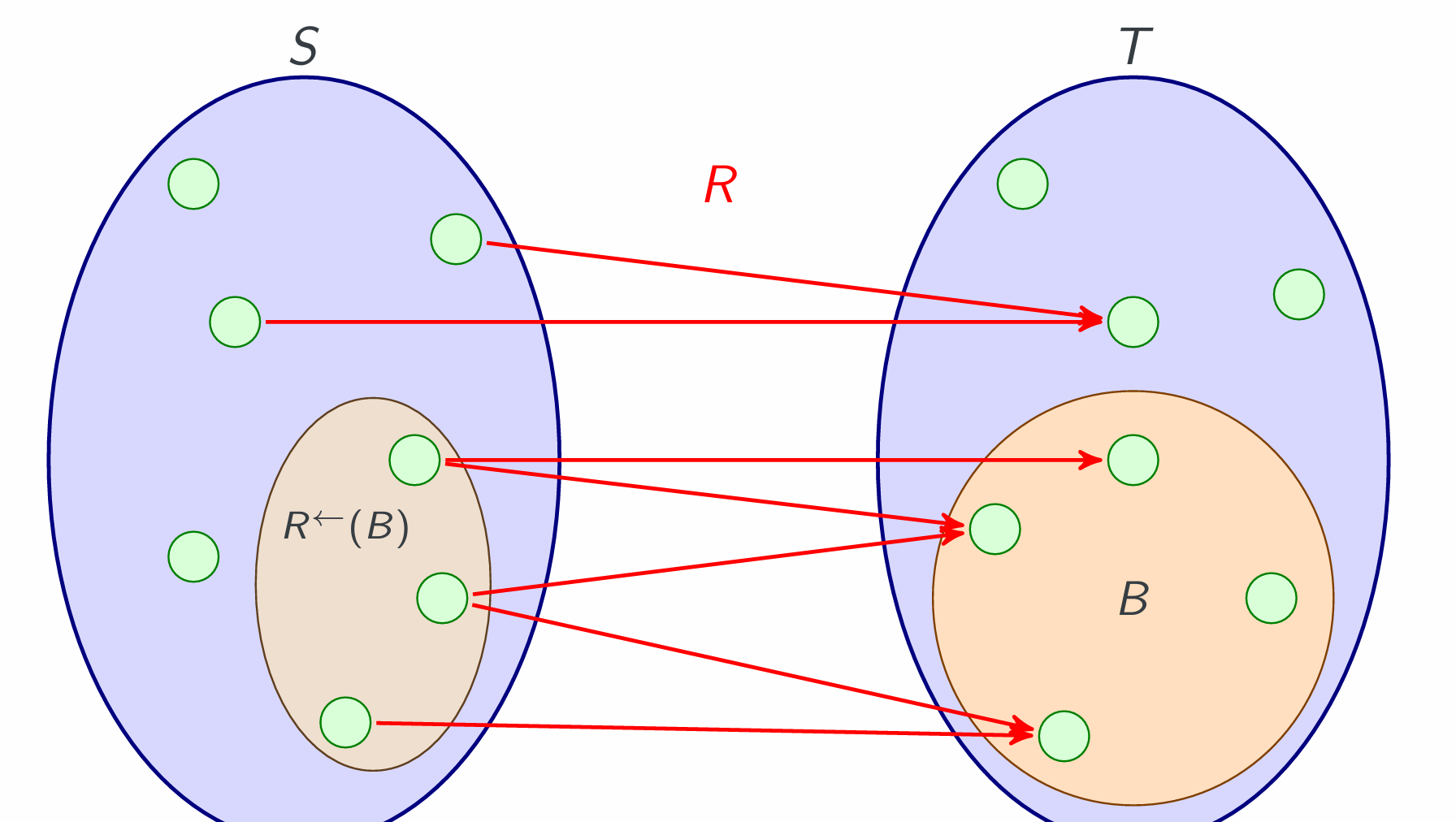
Given R ⊆ S ×T, A⊆S, and B ⊆T.
Relational image of A, R(A):
Relational pre-image of B, R←(B):
Personal understanding, R⊆S×T, image is a subset of S, pre-image is similar to converse relation, and its domain is subset of T. And the answer set is a set containing elements, rather not the pairs. The domain and co-domain are changed by $R(xxx)$ or $R^\leftarrow (xxx)$
Pay attention to the math expression writing, it is not R, it’s R(xx). What we learned in high school, the functions with its input range and output range, is exactly the images of functions.
Observe that the relational pre-image is the relational image of the converse relation.
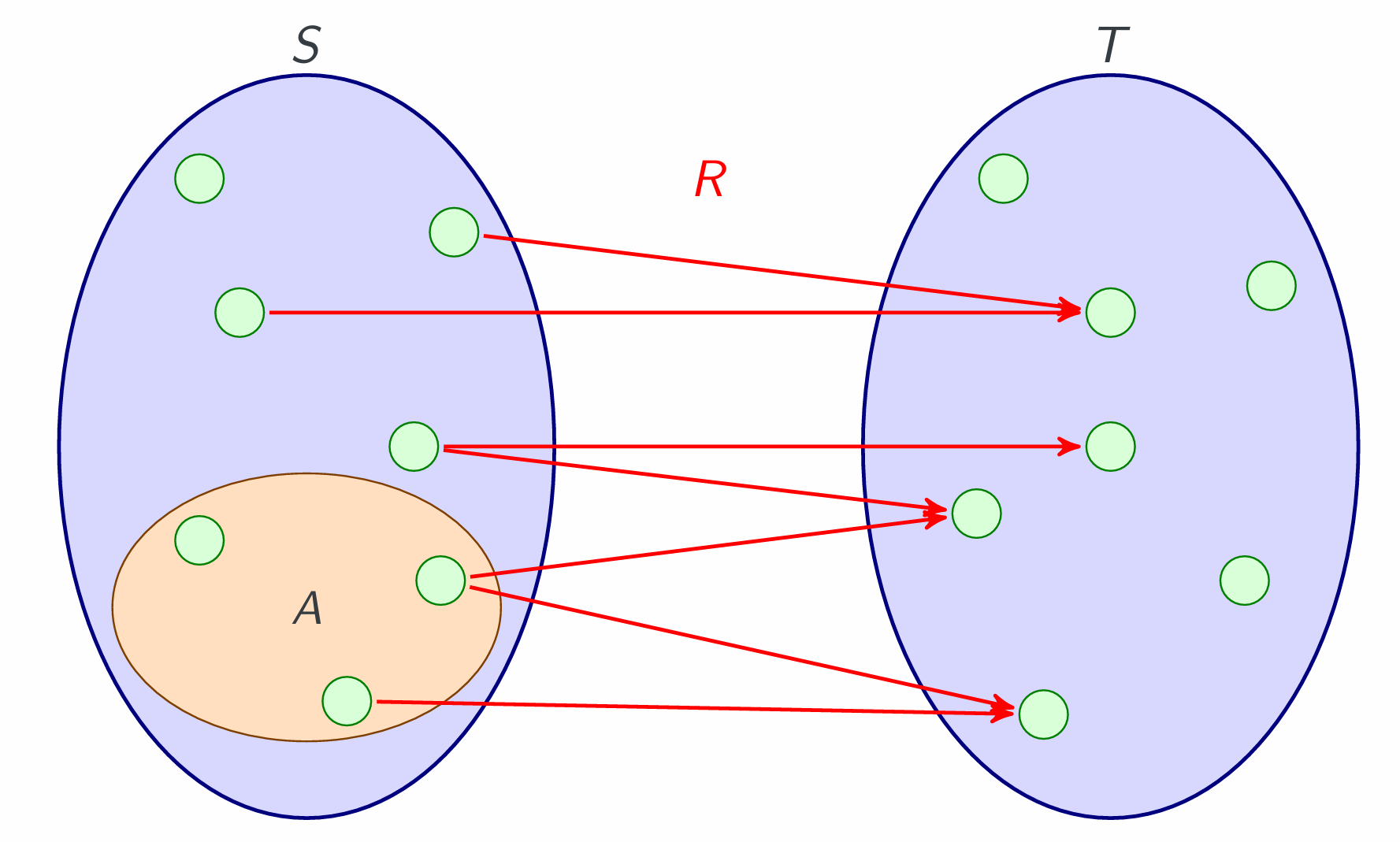
Relational image exercise
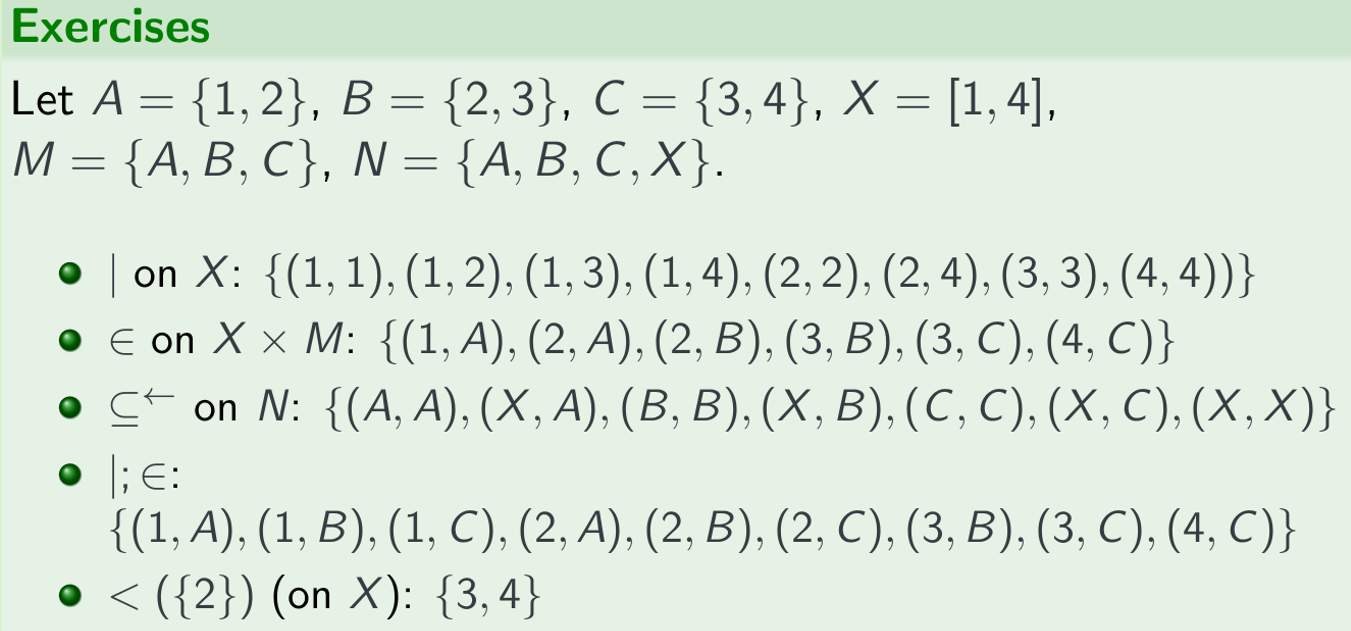
note: | is division, such as, 2 divides 4 and 6.
$\subseteq^\leftarrow : \quad\subseteq$ means subset, so $\subseteq^\leftarrow$ means superset.
$|;\in$ follows by
Composition: If R1⊆S×T and R2⊆T×U then R1;R2 ⊆ S×U:
Firstly, | and $\in$ mean that leftside is an element, and the right side is a set.
Secondly, | means the element can divide
<({2})(on X): {3,4}
Note it is a image on X. “on X” means XxX, and {2} is an image(or namely subset) of X, ‘<’ is relation, it’s looking forward to the set with image’s elements.
The domain and co-domain are always X, don’t understand it as {2}<X according to xRy, and it’s wrong, which means that {2} is the domain and X is the codomain.
It is image, and the concept above is almostly right but actually ‘on X’ means the domain and codomain are always still X according to the definition of image.
Properties of Binary Relations
Definition of five properties of Binary Relations (Fun) (Tot) (Inj) (Sur) (Bij) of $R \subseteq S \times T$
A binary relation $R⊆S×C$ is:
| Property | Name | Description |
|---|---|---|
| (Fun) | functional | For all s ∈ S there is at most one t ∈ T such that (s,t) ∈ R |
| (Tot) | total | For all s ∈ S there is at least one t ∈ T such that (s,t) ∈ R |
| (Inj) | injective | For all t ∈ T there is at most one s ∈ S such that (s,t) ∈ R |
| (Sur) | surjective | For all t ∈ T there is at least one s ∈ S such that (s,t) ∈ R |
| (Bij) | bijective | Injective and surjective |
Functions and function properties
Note, all of the five properties are not related to function directly, even functional (Fun) is not. The adjustives have different meanings with the function(noun). (Fun)’s domain is not required all the inputs of domain have a value. (Tot)’s input may have multiple values in the co-domain, hence they are not function directly.
(Fun) and (Tot) emphasize the domain, and (Inj), (Sur) and (Bij) emphasize the co-domain.
But if the adjectives are changed into noun with the suffix of ‘tion’, that means they are functions.
partial function is a binary relation that is (Fun).
A function is a binary relation that is (Fun) and (Tot).
An injection is a function that is (Inj).
A surjection is a function that is (Sur).
A bijection is a function that is (Bij).
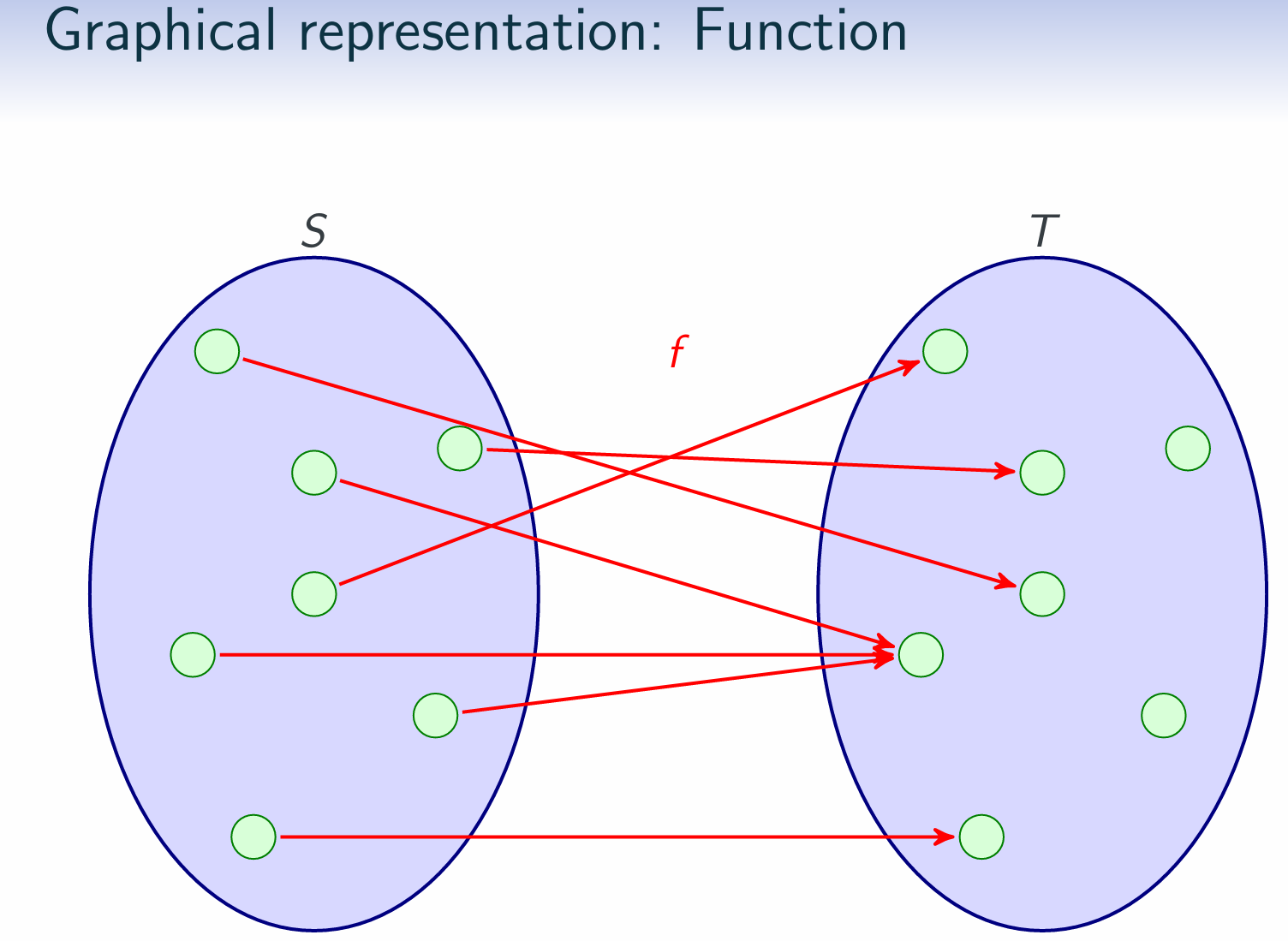
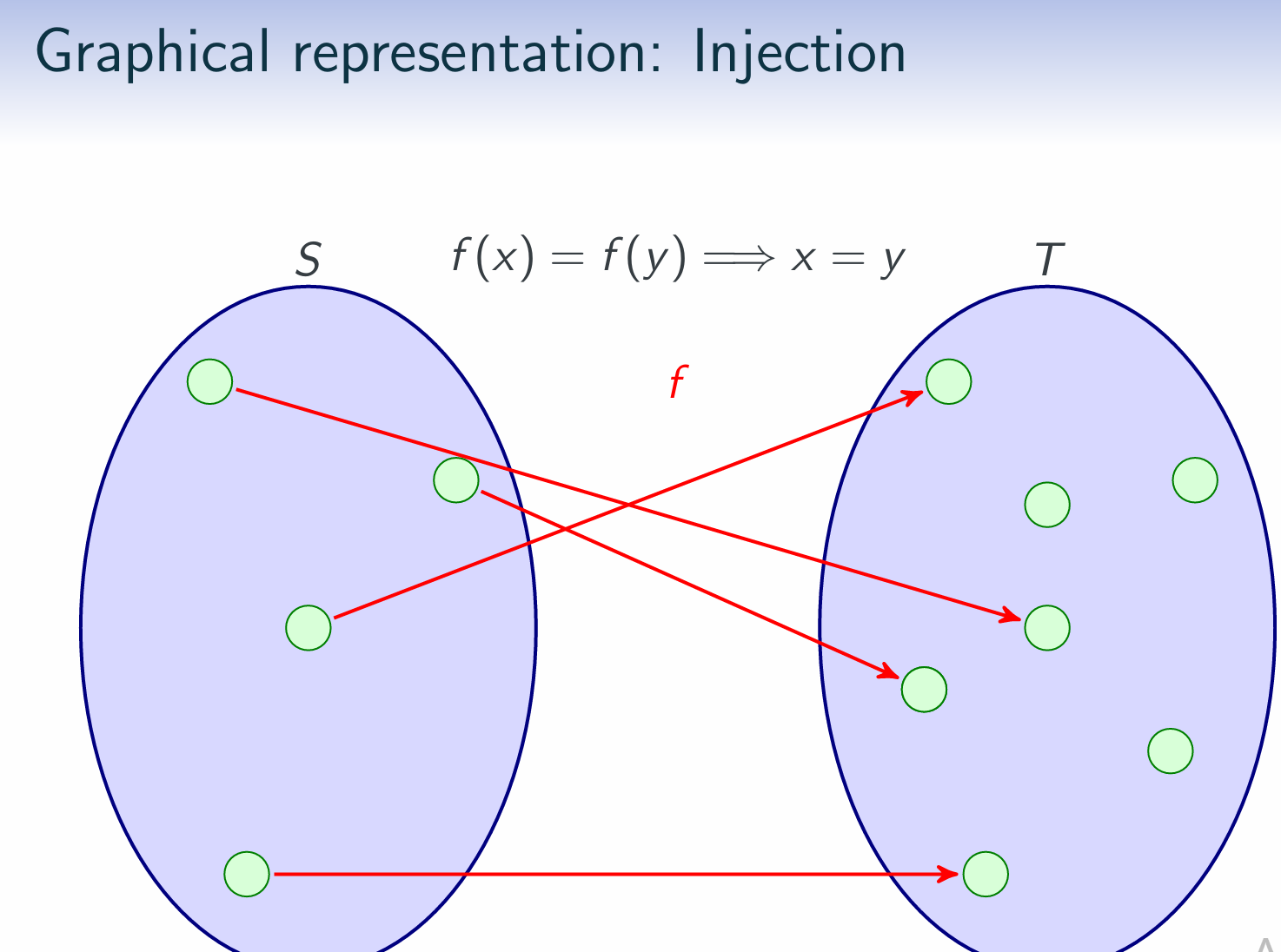
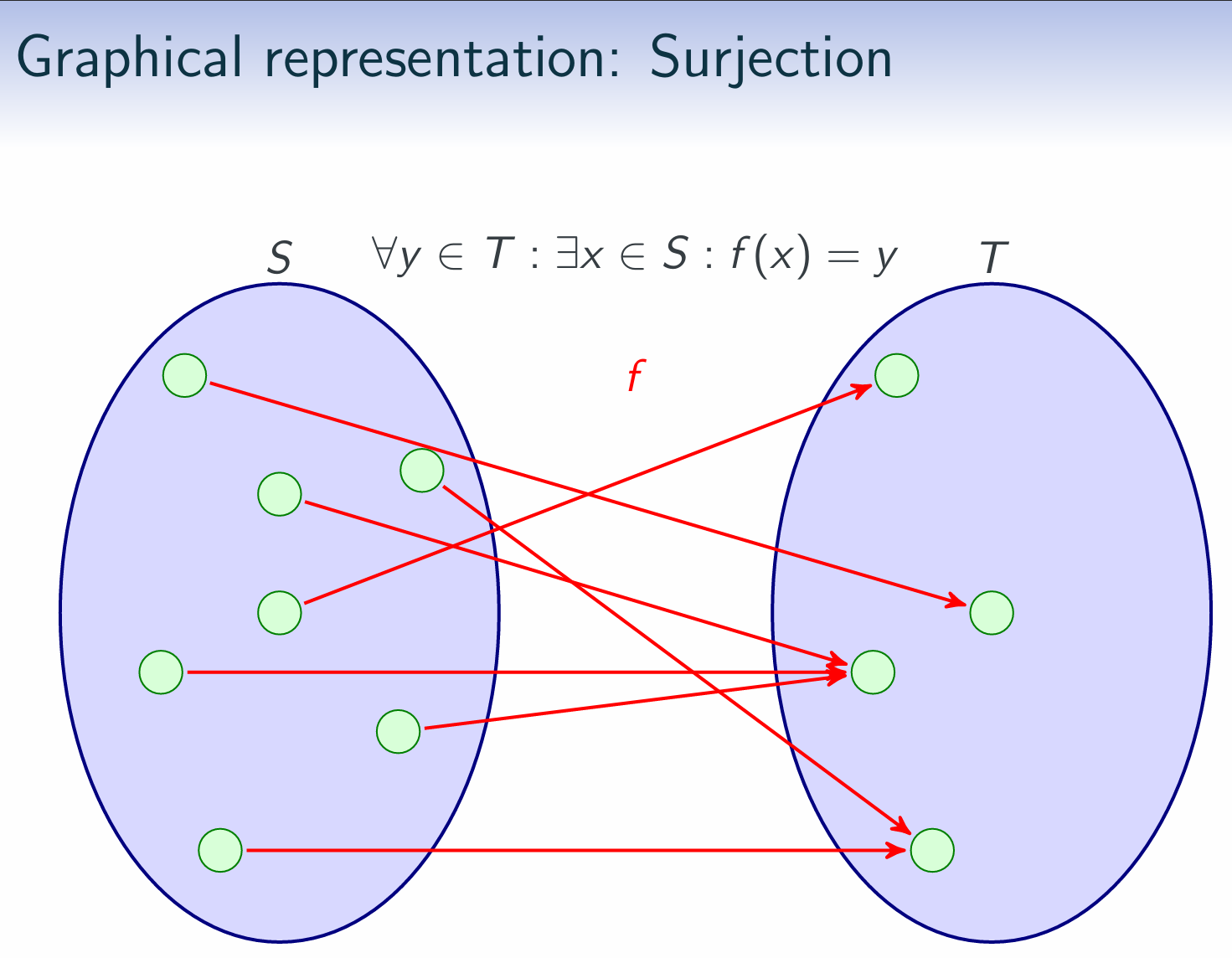
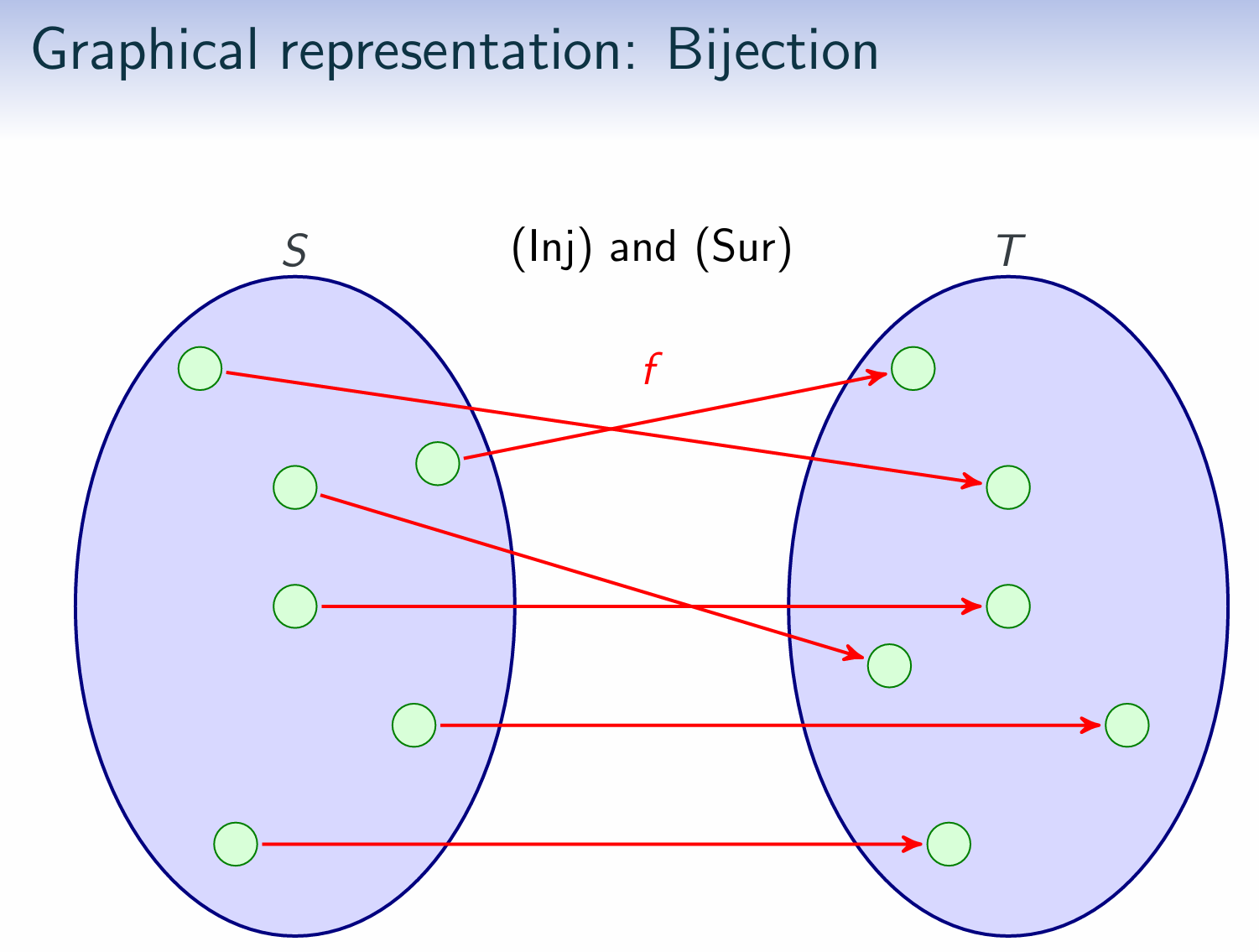
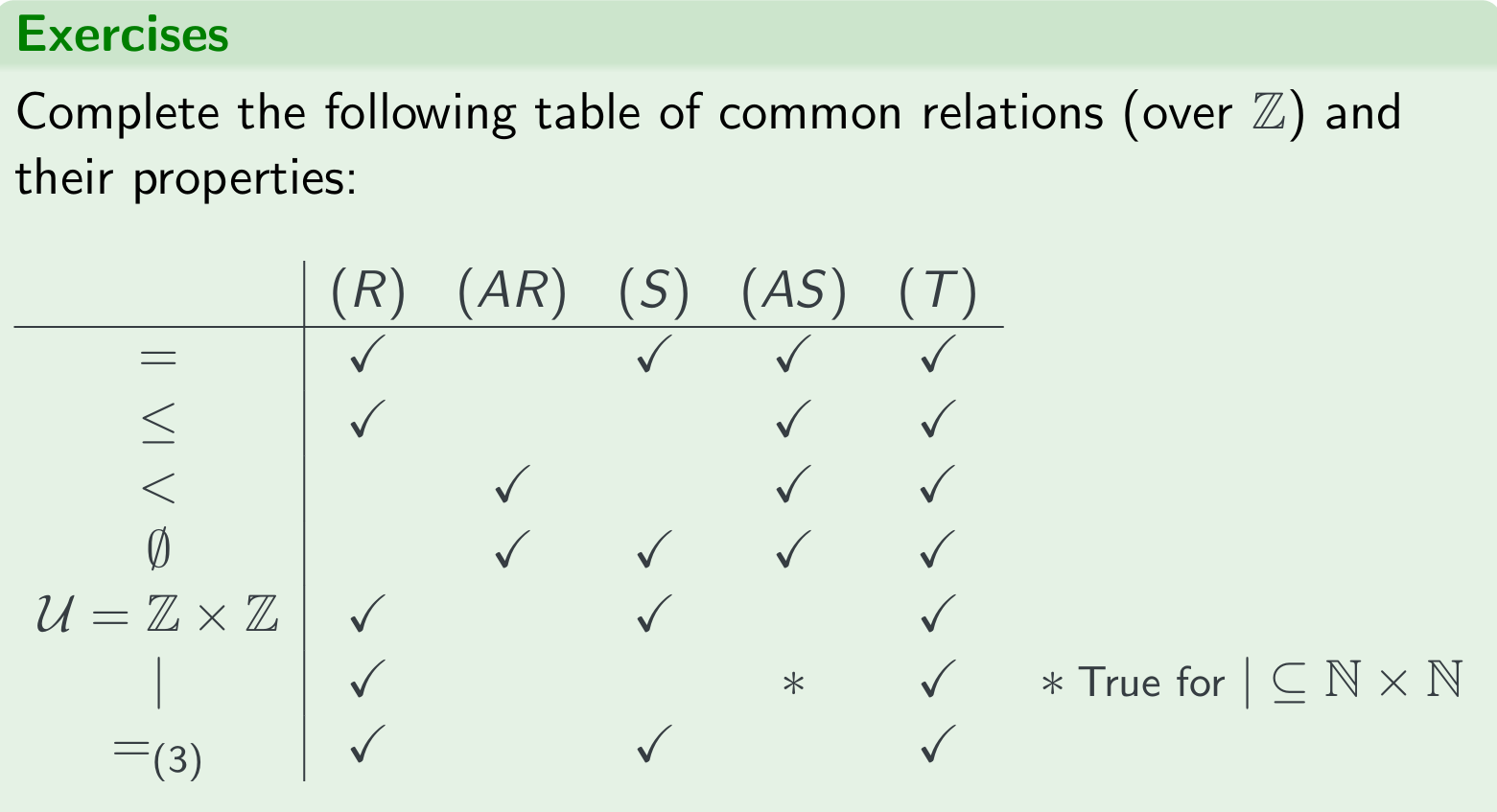
Properties of Binary Relations $R \subseteq S \times S$:(R)(AR)(S)(AS)(T)
Definition
| Property | Name | Description |
|---|---|---|
| (R) | reflexive | For all x ∈ S: (x,x) ∈ R |
| (AR) | antireflexive | For all x ∈ S: (x,x) ∉ R |
| (S) | symmetric | For all x,y ∈ S: If (x,y) ∈ R then (y,x) ∈ R |
| (AS) | antisymmetric | For all x,y ∈ S: If (x,y) and (y,x) ∈ R then x = y |
| (T) | transitive | For all x,y,z ∈ S: If (x,y) and (y,z) ∈ R then (x,z) ∈ R |
Identity: (diagonal, equality) I ={(x,x):x ∈ S }, it statisfy among reflexive and symmetric and antisymmetric.
Antisymmetric can contain the identity(part of symmetric).
Take Notice
- Properties have to hold for all elements
- (S), (AS), (T) are conditional statements – they will hold if there is nothing which satisfies the ‘if’ part
A relation can be both symmetric and antisymmetric. Namely, when R consists only of some pairs (x,x),x ∈ S.
A relation cannot be simultaneously reflexive and antireflexive (unless S = ∅).
For example, antisymmetric is different from non-symmetric. Antisymmetric means every elements hold that they dont have the symmetric pairs except their reflexive pairs. And antireflexive has the similar effects with antireflexive, antireflexive is different from non-reflexive.
Note the second notice, it satisfy the vacuous truth if there is nothing which satisfies.
examples by graph
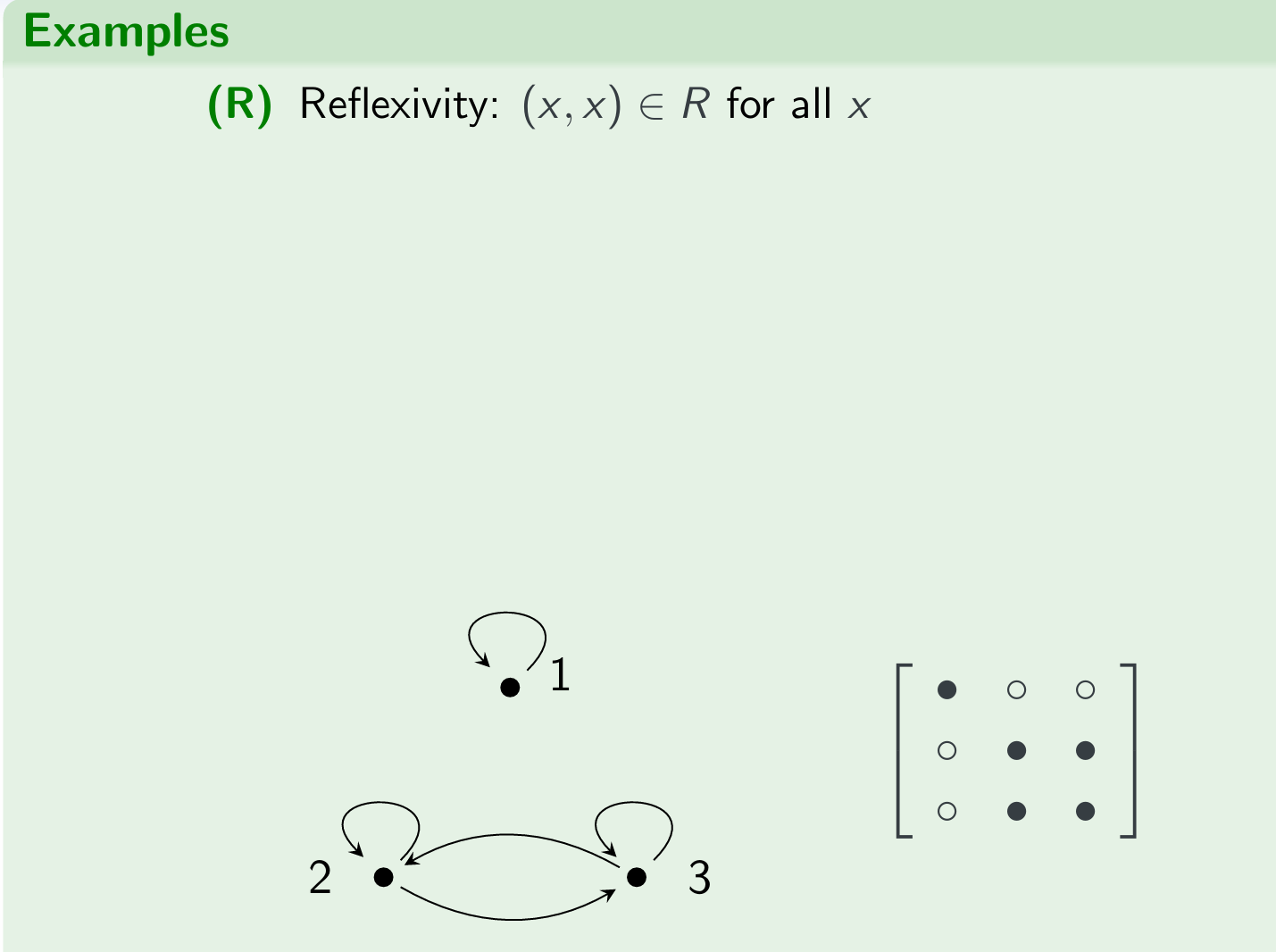

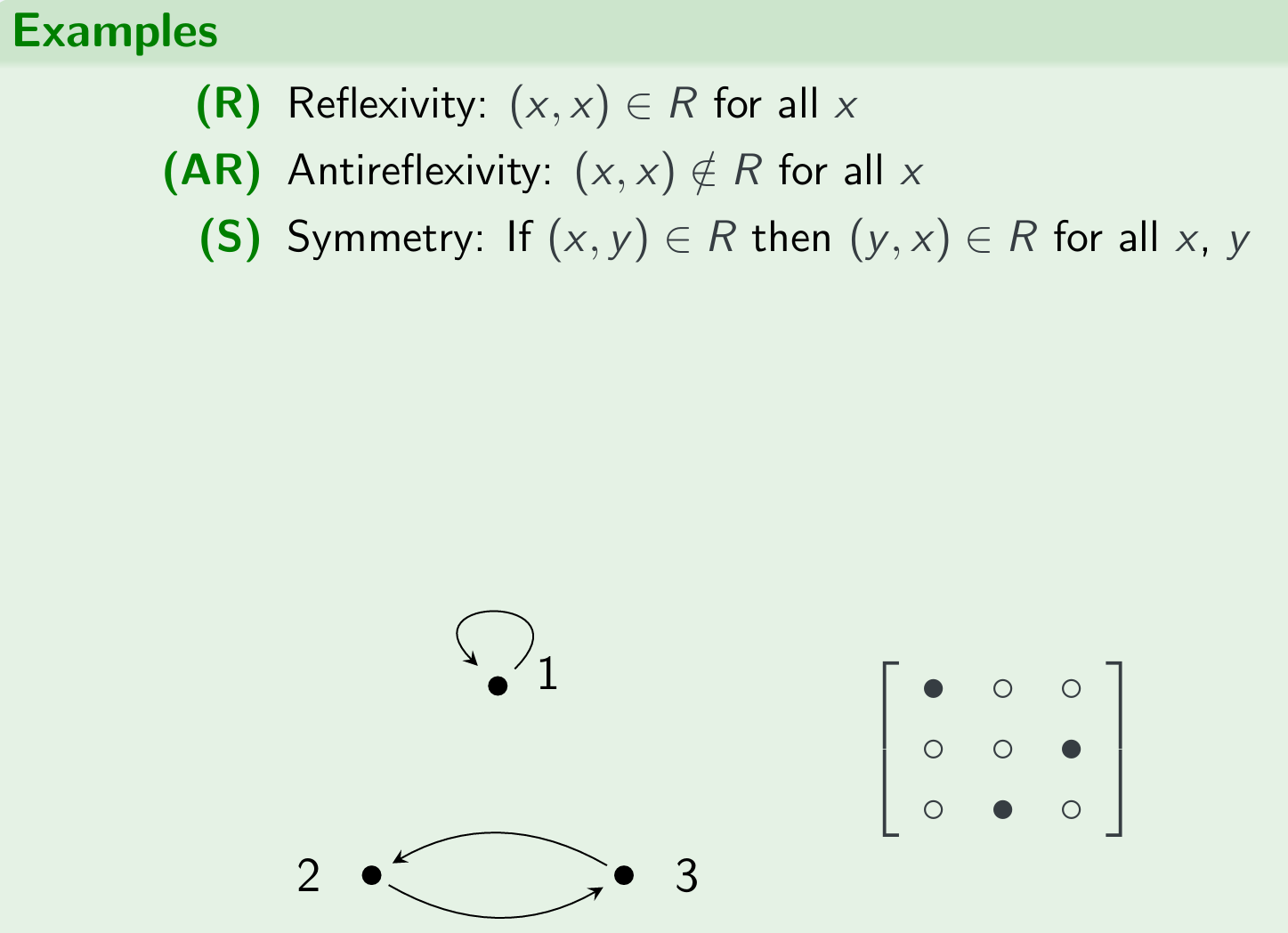
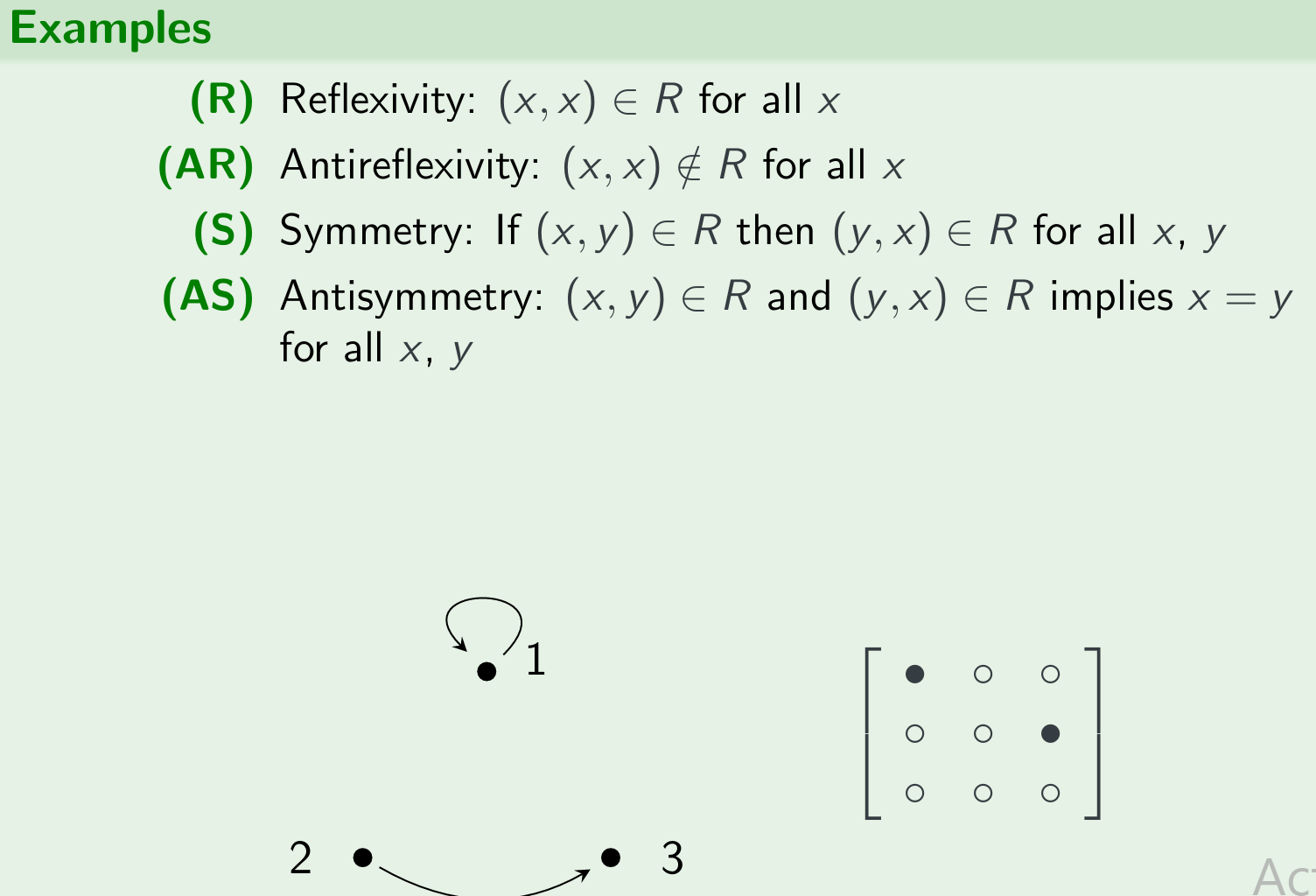
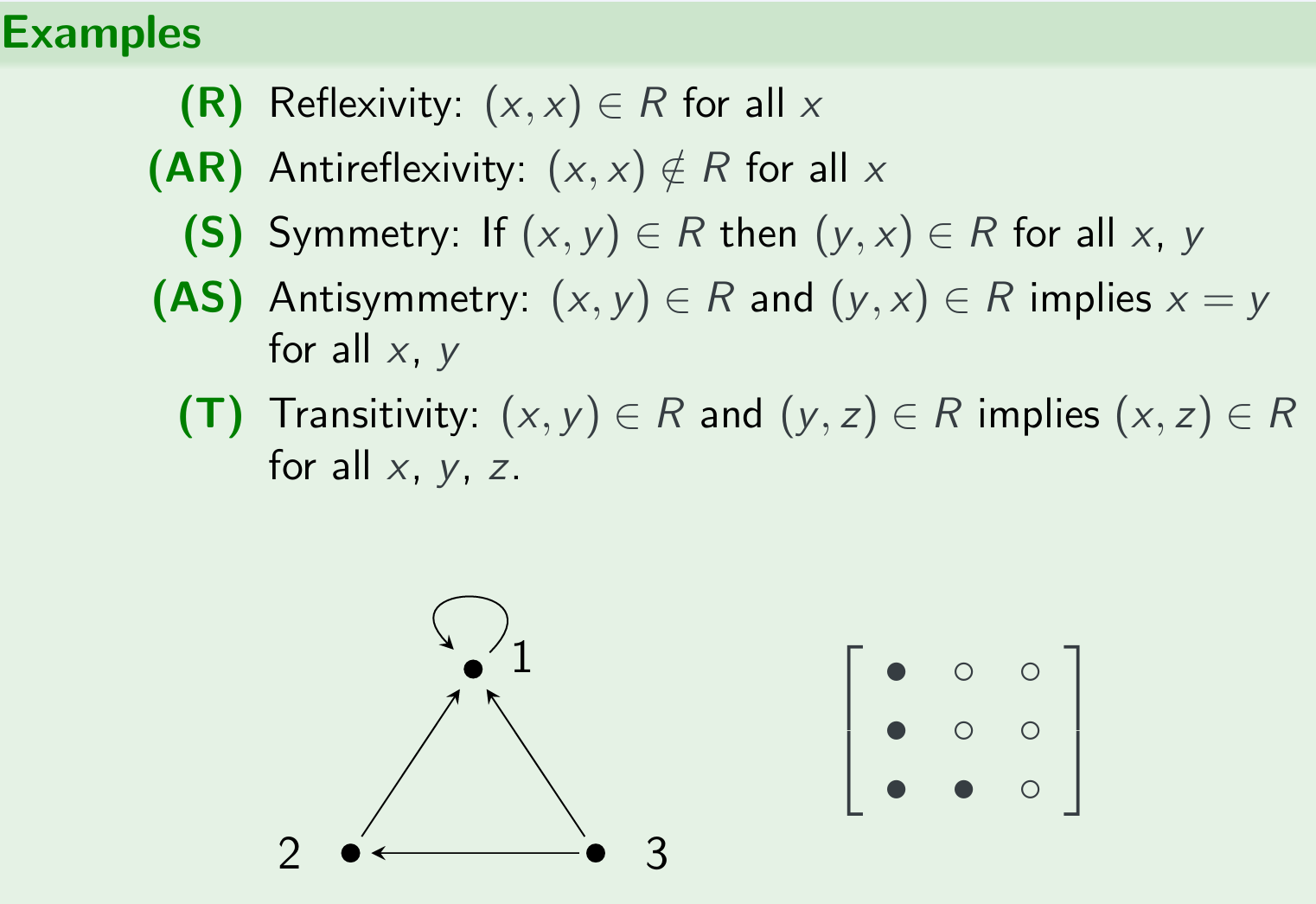
exercise
The following relations are on S = {1,2,3}. Which of the properties (R), (AR), (S), (AS), (T) does each satisfy?
(m,n) ∈ R if m+n =3? (AR) and (S)
(AR) and (S)
(m,n) ∈ R if max{m,n} = 3? (S)
(S)
Give examples of relations with specified properties.
(AS), (T), not (R)
Strict order of numbers x < y
≤ but with some pairs (x,x) removed
Being a prime divisor: (p,n) ∈ R iff p is prime and p|n
- Not reflexive: (1,1) / ∈ R
- Transitivity is meaningful only for the pairs (p,p),(p,n) p|n for p prime
(S), not (R), not (T)
- Simplest example- inequality
$\mathbb{N} \times \mathbb{N}$ is a set of pairs, such as ((1,2),(2,3)). It demands that $(m,n)R(p,q)$ if $ m \equiv p \pmod{3} $ or $n \equiv q \pmod{5}$
(a) Is R reflexive?
Yes: m =(3) m so (m,n)R(m,n).
(b) Is R symmetric?
Yes: by symmetry of · =(n) ·.
(c) Is R transitive?
No: Consider (1,1), (1,4) and (2,4).
Analysis
R is a relation on $\mathbb{N} \times \mathbb{N}$, i.e. it is a subset of $\mathbb{N}^2 \times \mathbb{N}^2$
$(m,n)R(p,q)$ if $m \underset{(3)}{=} p$ or $n \underset{(5)}{=} q$
And then you would easily know the options a and b
How to prove option c?
Notice that the pairs of the two point pairs, it uses OR to connect. We can find (0,0)R(0,1) is right, and (0,1)R(1,1) is right, but (0,0)R(1,1) is obviously wrong.
Functions
Definition
A function, f : S → T, is a binary relation f ⊆ S×T that satisfies (Fun) and (Tot). That is, for all s ∈ S there is exactly one t ∈ T such that (s,t) ∈ f.
We write f(s) for the unique element related to s.
We write $T^S$ for the set of all functions from S to T.
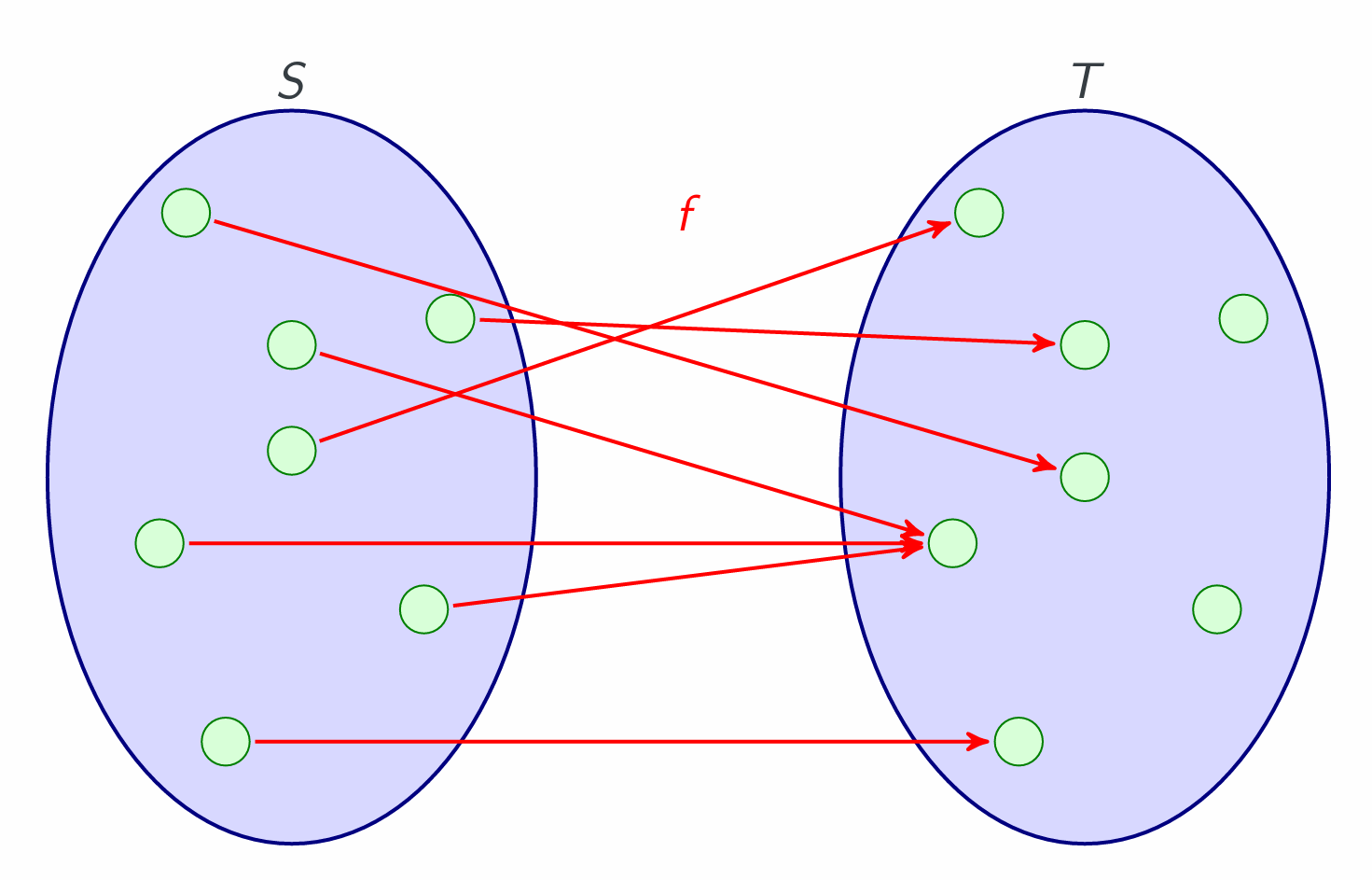
f : S →T describes pairing of the sets: it means that f assigns to every element s ∈ S a unique element t ∈ T. To emphasise where a specific element is sent, we can write f : x → y, which means the same as f(x) = y
| Symbol | Symbol | Symbol | Description |
|---|---|---|---|
| S | domain of f | Dom(f) | (inputs) |
| T | co-domain of f | Codom(f) | (possible outputs) |
| f(S) | image of f | Im(f) | (actual outputs) |
| S | domain of f | Dom(f) | (inputs) |
={f(x):x ∈ Dom(f) } is original in slides, I omit it in my write up. It looks like to describe f(S), and I guess it may be a typo: it should be ={f(x):x ∈ Dom(S) }.
f is a relation with domain and co-domain, and f(S) constrain the subset of domain, and f(S) means the actual output set (all output in the set can find its intput in pre-image ).
Important! The domain and co-domain are critical aspects of a function’s definition.
and
are different functions even though they have the same behaviour!
Converse of a function
Q: $f^\leftarrow$ is a relation; when is it a function?
A: When f satisfies (Inj) and (Sur)– i.e. when f is a bijection.
Properties of bijections
Suppose f : S → T and g : T →U are bijections
Fact
$f^\leftarrow: T \rightarrow S$ and $g^\leftarrow: U \rightarrow T$ are bijections
$(f ; g) : S → U$ is a bijection
$f;f^\leftarrow = I_S = {(x,x) : x ∈ S}$ and $f^\leftarrow;f=I_T={(x,x) : x ∈ T}$
Fact
f : S →T is a bijection if and only if there is a g : T → S such that $f;g=I_S$ and $g;f=I_T$
Welcome to point out the mistakes and faults!