Last week Paul took 3 lectures to teach the relations. The concepts are a little many for newers, and I spent 4 days to understand what he taught.
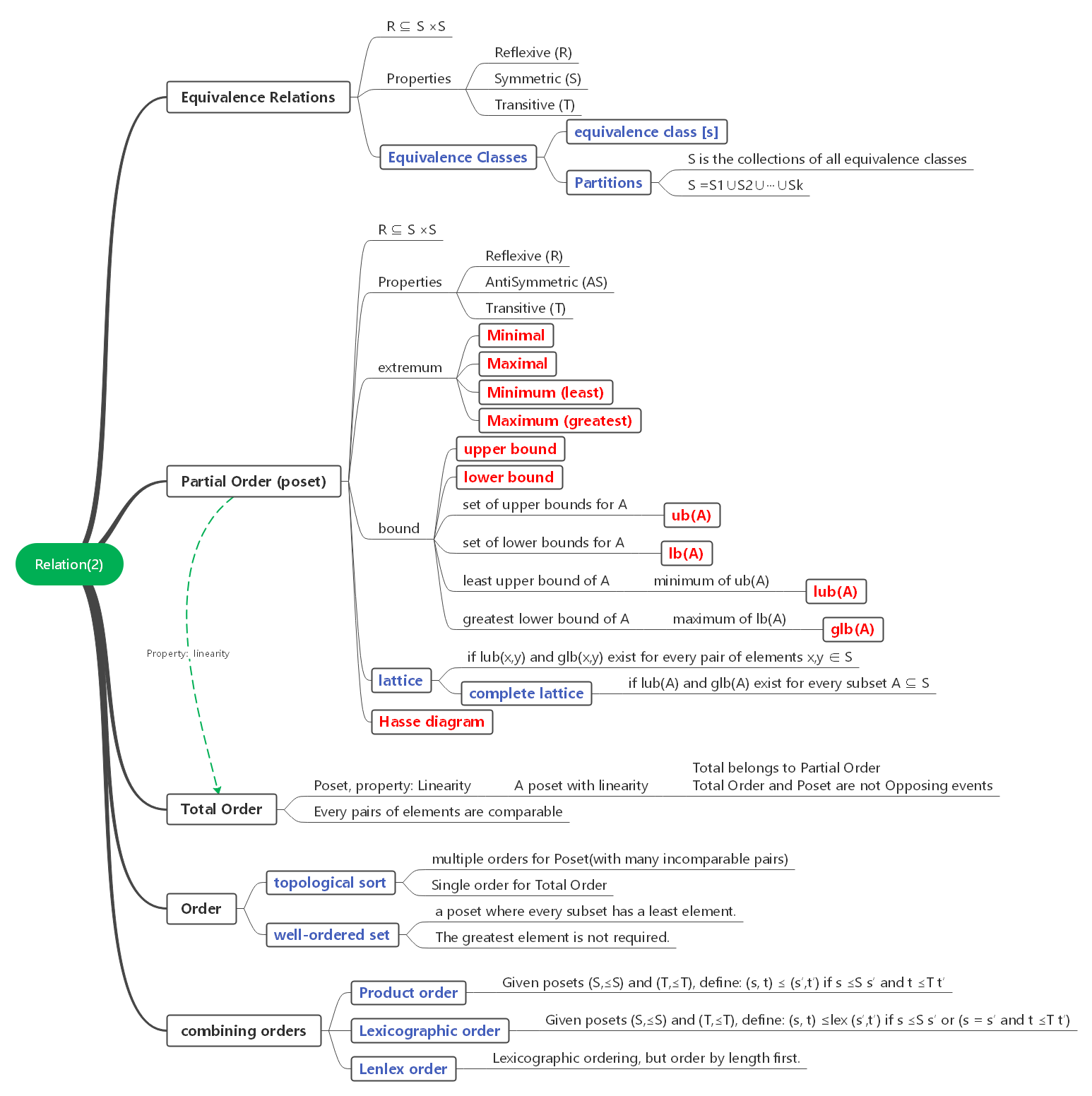
- Equivalence Relations (R)(S)(T)
- Equivalence Classes
- Partitions
- Partial Orders (R),(AS),(T)
- Hasse diagram
- Ordering
- Total orders
- Ordering of a Poset
Equivalence Relations (R)(S)(T)
Equivalence relations capture a general notion of “equality”. They are relations which are:
Reflexive (R): Every object should be “equal” to itself
Symmetric (S): If x is “equal” to y, then y should be “equal” to x
Transitive (T): If x is “equal” to y and y is “equal” to z, then x should be “equal” to z.
definition of Equivalence Relation
A binary relation R ⊆ S ×S is equivalence relation if it satisfies (R), (S), (T).
Equivalence Classes
Suppose R ⊆ S ×S is an equivalence relation
The equivalence class [s] (w.r.t. R) of an element s ∈ S is
Fact
s R t if and only if [s] = [t].
Partitions
A partition of a set S is a collection of sets $S_1, \dots, S_k$ such that
The collection of all equivalence classes {[s] : s ∈ S} forms a partition of S.
In the opposite direction, a partition of a set defines the equivalence relation on that set. If $S = S_1 \cup S_2 \cup \dots \cup S_k$, then we can define $\sim \subseteq S \times S$ as
examples
Q: Show that $m ∼ n$ iff $m^2 \underset{(5)}{=} n^2$ is an equivalence on
A:
It just means that $m \underset{(5)}{=} n$ or $m \underset{(5)}{=} -n$
e.g. $1 \underset{(5)}{=} -4$
This satisfies (R), (S), (T).
Find all the equivalence classes.
We have
[1] = {1,4,6},
[2] = {2,3,7},
[5] = {5}
Partial Orders (R),(AS),(T)
A partial order $\preceq$ on S satisfies (R),(AS),(T)
We call $(S, \preceq)$ a poset — partially ordered set
examples
Posets:
Not posets:
Hasse diagram
Every finite poset (S,⪯) can be represented with a Hasse diagram:
Nodes are elements of S
An edge is drawn upward from x to y if x ≺ y and there is no z such that x ≺ z ≺ y
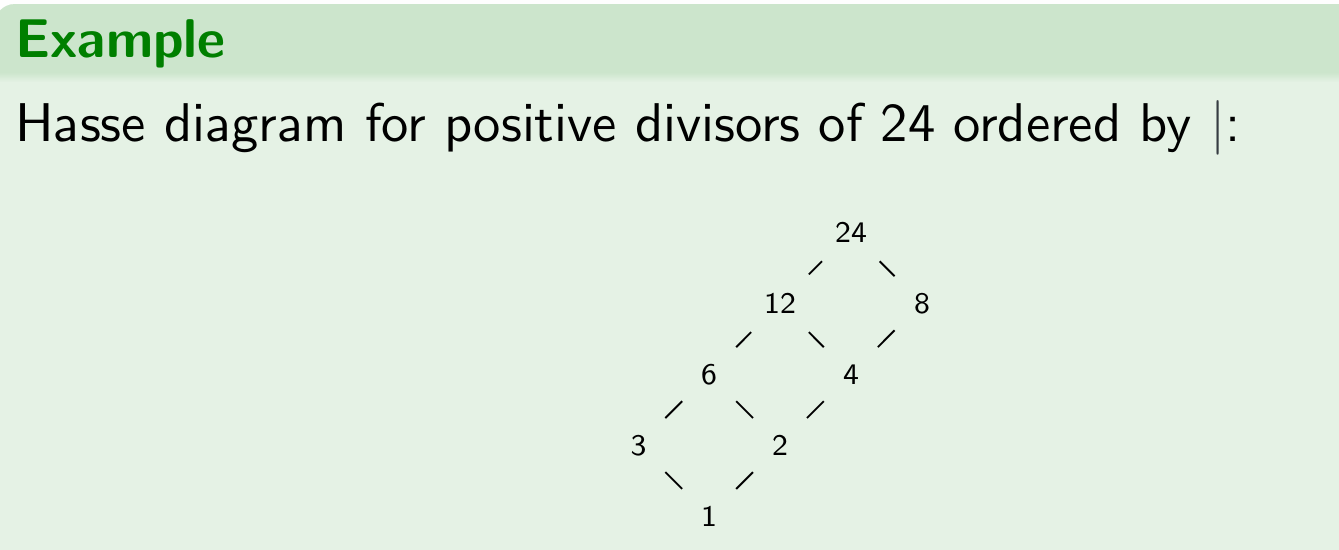
Ordering
Minimal, Maximal, Minimum, Maximum
Let (S,⪯) be a poset.
Minimal element: x such that there is no y= x with y ⪯ x
Maximal element: x such that there is no y= x with x ⪯ y
Minimum (least) element: x such that x ⪯ y for all y ∈ S
Maximum (greatest) element: x such that y ⪯ x for all y ∈S
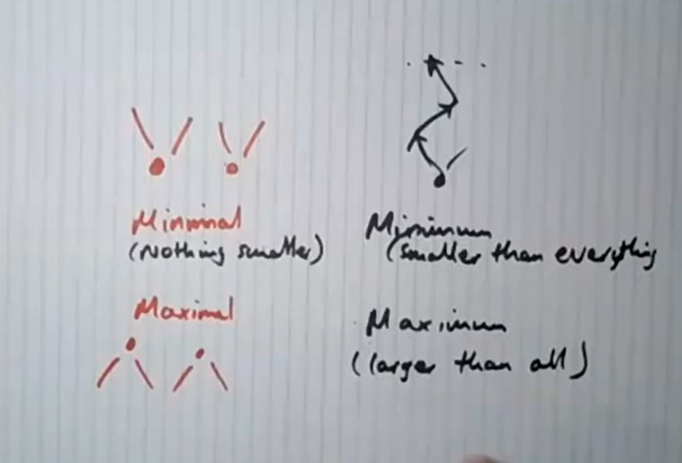
Take Notice
There may be multiple minimal/maximal elements.
Minimum/maximum elements are the unique minimal/maximal elements if they exist.
Minimal/maximal elements always exist in finite posets, but not necessarily in infinite posets.
Examples
Pow({a,b,c}) with the order ⊆, ∅ is minimum; {a,b,c} is maximum
Pow({a,b,c}) \ {{a,b,c}} (proper subsets of {a,b,c}). Each two-element subset {a,b},{a,c},{b,c} is maximal. But there is no maximum
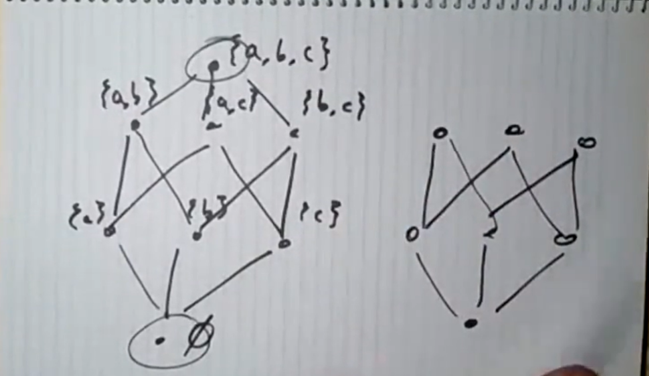
upper bound, lower bound, lub, glb
Let (S,⪯) be a poset.
x is an upper bound for A if a ⪯ x for all a ∈ A
x is a lower bound for A if x ⪯ a for all a ∈ A
The set of upper bounds for A is defined as ub(A) = {x : a ⪯ x for all a ∈ A}
The set of lower bounds for A is defined as lb(A) = {x : x ⪯ a for all a ∈ A}
The least upper bound of A, lub(A), is the minimum of ub(A) (if it exists)
The greatest lower bound of A, glb(A) is the maximum of lb(A) (if it exists)
lub, glb
To show x is glb(A) you need to show:
x is a lower bound: x ⪯ a for all a ∈ A.
x is the greatest of all lower bounds: If y ⪯ a for all a ∈ A then y ⪯ x
Example
Pow(X) ordered by ⊆.
glb(A,B) = A∩B
lub(A,B) = A∪B
lattice and complete lattice
Let (S,⪯) be a poset.
- (S,⪯) is a lattice if lub(x,y) and glb(x,y) exist for every pair of elements x,y ∈ S.
- (S,⪯) is a complete lattice if lub(A) and glb(A) exist for every subset A ⊆ S.
Take Notice
A finite lattice is always a complete lattice.
An infinite lattice need not have a lub (or no glb) for an arbitrary infinite subset of its elements, in particular no such bound may exist for all its elements.
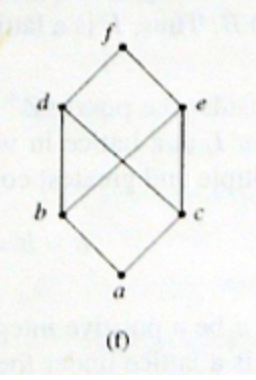
For the pic below, for (b,c), {e,d,f} are the upper bounds, but there is no minimum of the ub. Hence lub doesnot exist, it is not a lattice.
it is not a lattice. for (e,d), b,c,a are the minimals, but they are not the minimum.
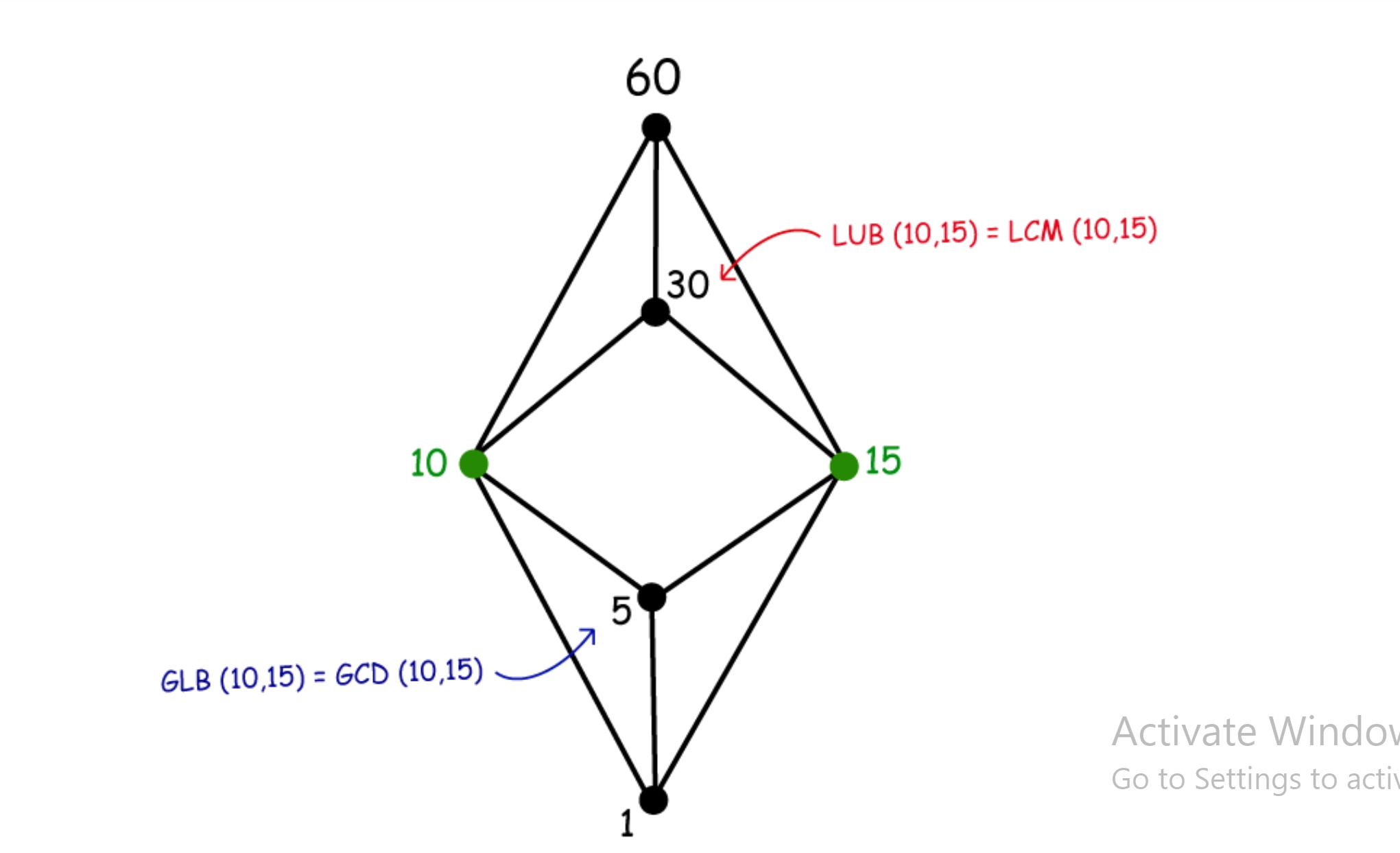
is 30 the lub(5,15)? yes! is it a lattice? Yes, because it is finite.
who is the lb({10,30})? it is 10! And 10 is also glb({10,30})! Remember the poset can include themselves.
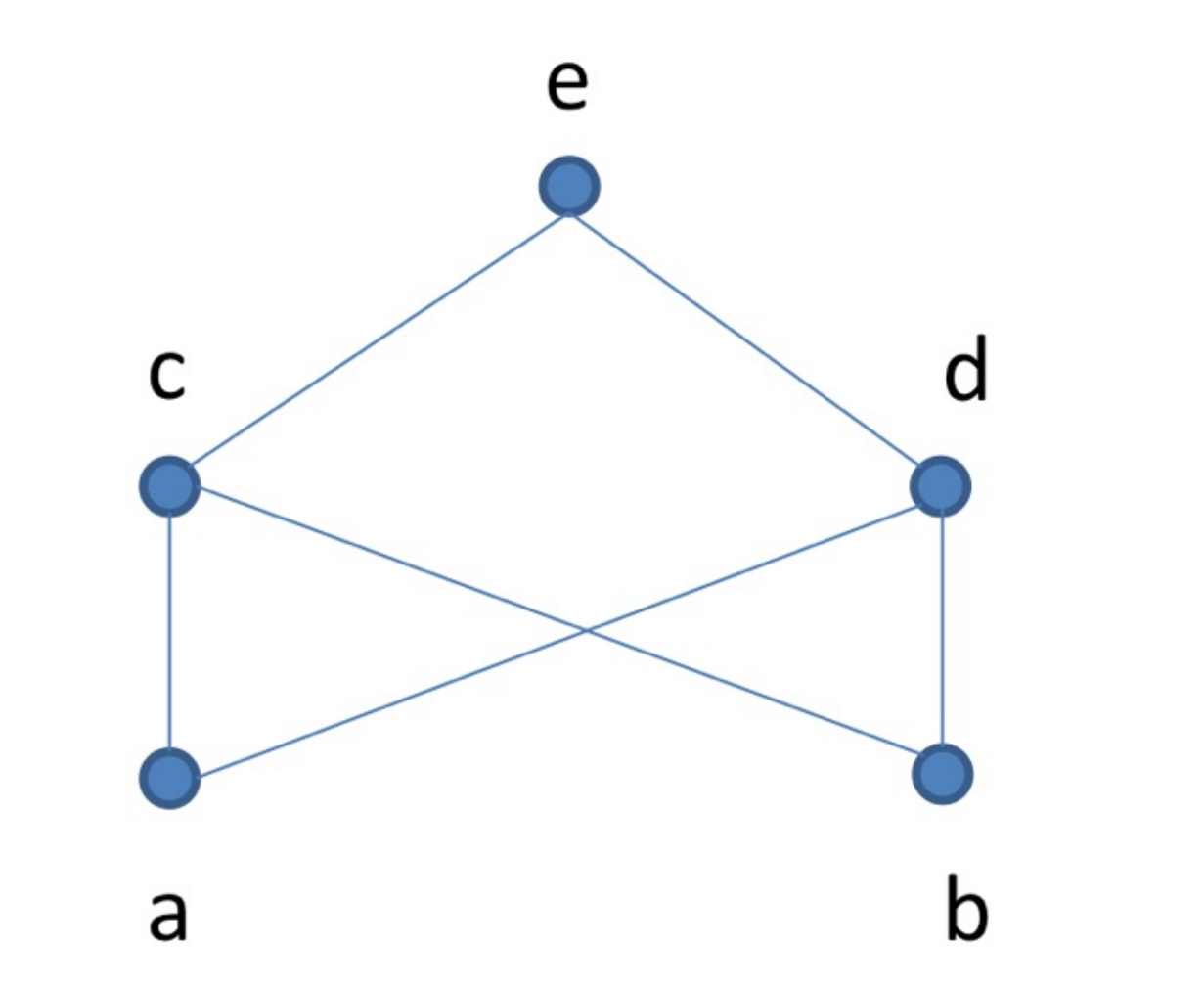
not a lattice obviously.
example
Q
{1,2,3,4,6,8,12,24} partially ordered by divisibility is a lattice
- e.g. lub({4,6}) = 12; glb({4,6}) = 2
{1,2,3} partially ordered by divisibility is not a lattice
- {2,3} has no lub
{2,3,6} partially ordered by divisibility
- {2,3} has no glb
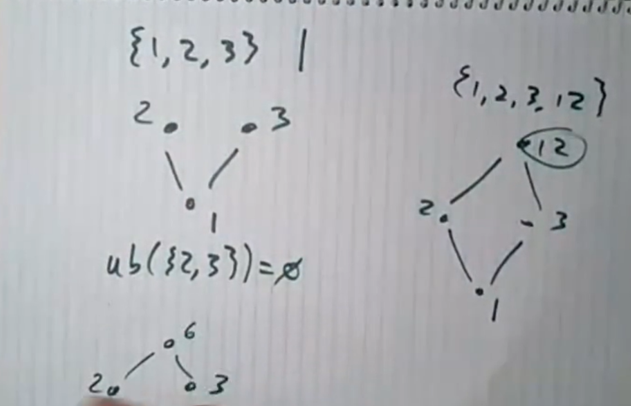
{1,2,3,12,18,36} partially ordered by divisibility
- {2,3} has no lub (12,18 are minimal upper bounds)
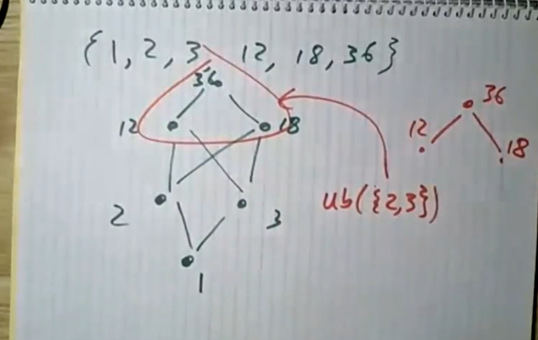
Q
(Z,≤): neither lub(Z) nor glb(Z) exist
(F(N),⊆) [all finite subsets of N]: lub exists for pairs of elements but not generally for (infinite) sets of elements. glb exists for any set of elements: intersection of a set of finite sets is finite.
(I(N),⊆) [all infinite subsets of N]: glb does not exist for some pairs of elements (e.g. odds and evens). lub exists for any set of elements: union of a set of infinite sets is always infinite.
Q: Considerposet(R,≤)
(a) Is this a lattice?
(b) Give an example of a non-empty subset of R that has no upper bound.
(c) Find lub({ x ∈ R:x < 73 })
(d) Find lub({ x ∈ R:x ≤ 73 })
(e) Find lub( x :$x^2$ < 73 )
(f) Find glb( x :$x^2$ < 73 )
A:
Yes
{ r ∈R:r >0}
=(0,∞)
73
73
√73
−√73
Total orders
A total order is a partial order that also satisfies:
(L) Linearity (any two elements are comparable):
For all x,y either: x ≤ y or y ≤ x (or both if x = y)
Take Notice
On a finite set all total orders are “isomorphic”
On an infinite set there is quite a variety of possibilities.
example
Z with ≤:
(no minimum/maximum element)
Z with {(x,y) : (xy ≤ 0 and x ≤ y) or (xy > 0 and |x| ≤ |y|)}:
(no maximum element, minimum element is-1)
Z with {(x,y) : (xy ≤ 0 and x ≥ y) or (xy > 0 and x ≤ y)}:
(minimum element 1, maximum element-1)
Ordering of a Poset
Topological Sort
For a poset (S,⪯) any total order ≤ that is consistent with ⪯ (if a ⪯b then a ≤b) is called a topological sort.
Consider
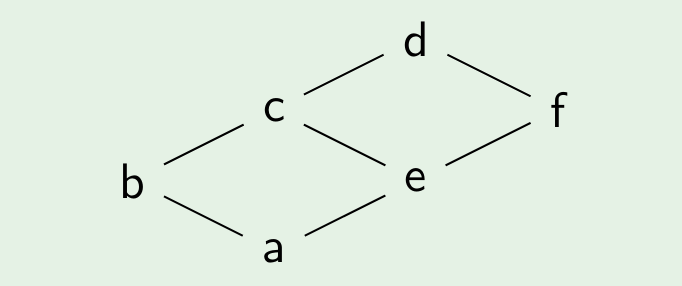
The following all are topological sorts:
a ≤ b ≤ e ≤ c ≤ f ≤d
a ≤ e ≤ b ≤ f ≤ c ≤d
a ≤ e ≤ f ≤ b ≤ c ≤d
all of these orders are right
Well-Ordered Sets
A well-ordered set is a poset where every subset has a least element
Take Notice
The greatest element is not required.
Well-ordered sets are an important mathematical tool to prove termination of programs.
Examples
Disjoint union of copies of $\mathbb{N}$:
where each Ni ≃ N and N1 < N2 < N3···
Cartesian products
Product order: Given posets $(S,⪯_S)$ and $(T,⪯_T)$, define:
(s, t) ⪯ (s’,t’) if s $⪯_S$ s′ and t $⪯_T$ t’
Notes
No implicit weighting.
No bias toward any component.
In general, it is only a partial order, even if combining total orders.
Which cannot compare contray s and t:

Lexicographic order
Given posets (S,$⪯S$) and (T,$⪯_T$), define:
(s, t) $≤{lex}$ (s′,t′) if s $⪯_S$ s′ or (s = s′ and t $⪯_T$ t′)
Extension to words: $λ ≤_{lex} w$ for all words
Notes
No implicit weighting.
Gives total order when combining total orders.
Can be sensibly extended to words.
Not ideal for enumeration.
Lenlex order
Lexicographic ordering, but order by length first.
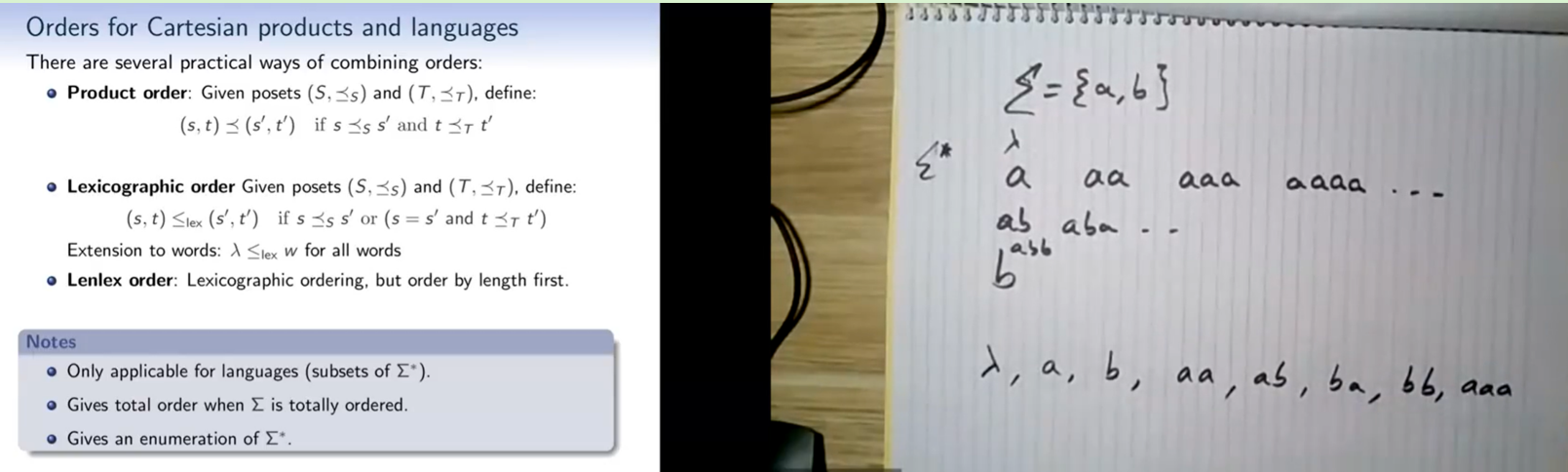
Notes
Only applicable for languages (subsets of $Σ^∗$).
Gives total order when Σ is totally ordered.
Gives an enumeration of $Σ^∗$.
example for above
Q
Let $\mathbb{B}$={0,1} with the usual order 0<1. List the elements 101,010,11,000,10,0010,1000 of $\mathbb{B}^*$ in the
(a) Lexicographic order
000,0010,010,10,1000,101,11
(b) Lenlex order
10,11,000,010,101,0010,1000
Q:
Whenarethelexicographic order and lenlex on $Σ^∗$ the same?
Only when $|Σ| = 1$.
Q: Trueor false?
(a) If a set Σ is totally ordered, then the corresponding lexico graphic partial order on $Σ^∗$ also must be totally ordered.
True
(b) If a set Σ is totally ordered, then the corresponding lenlex order on $Σ^∗$ also must be totally ordered.
True
(c) Every finite poset has a Hasse diagram.
True
(d) Every finite poset has a topological sorting.
True
(e) Every finite poset has a minimum element.
False
(f) Every finite totally ordered set has a maximum element.
True
(g) An infinite poset cannot have a maximum element.
False
Welcome to point out the mistakes and faults!