PREFACE

• Functions Recap
  • five properties fun-tot-inj-sur-bij
  • Definition of function
    • example
  • Injective functions
    • Examples
      • functions that are injective
      • functions that are not injective
  • Surjective functions
    • Examples
      • functions that are surjective
      • functions that are not surjective
  • Bijection functions
  • Functions on finite sets
• Functional Composition
  • Definition
  • Iteration of Functions
  • exercise
• Inverse Functions
  • Properties of the inverse
    • Exercises
• Matrices
  • Matrix Motivation
  • Basic Matrix Operations
  • Matrix Sum
  • Scalar Product
  • Matrix Product
• \end{bmatrix}
  • Computer Graphics
• Introduction to Big-O Notation
  • Motivation
    • example: Algorithmic analysis
  • “Big-O” Asymptotic Upper Bounds
    • example
  • properties
    • example
  • “Big-Omega” Asymptotic Lower Bounds
    • Example
  • “Big-Theta” Notation
    • Properties
    • Observations
      • Examples
      • Exercises

Functions Recap

five properties fun-tot-inj-sur-bij

binary relation’s five properties: fun-tot-inj-sur-bij

Definition of function

A function, f : S → T, is a binary relation f ⊆ S ×T that satisfies (Fun) and (Tot). That is, for all s ∈ S there is exactly one t ∈ T such that (s,t) ∈ f.

We write f(s) for the unique element related to s.

We write $T^S$ for the set of all functions from S to T.

f : S →T describes pairing of the sets: it means that f assigns to every element s ∈ S a unique element t ∈ T. To emphasise where a specific element is sent, we can write f : x → y, which means the same as f(x) = y

Symbol	Symbol	Symbol	Description
S	domain of f	Dom(f)	(inputs)
T	co-domain of f	Codom(f)	(possible outputs)
f(S)	image of f	Im(f)	(actual outputs)
S	domain of f	Dom(f)	(inputs)

example

The identity function on S

$$Id_S(x) = x,x ∈ S$$ $$Dom(Id_S) = S \\ Codom(Id_S) = S \\ Im(Id_S) = S$$

Important!

The domain and co-domain are critical aspects of a function’s definition.

$f: \mathbb{N} \rightarrow \mathbb{Z}$ given by $f(x)=x^2$

and

$g: \mathbb{N} \rightarrow \mathbb{N}$ given by $g(x)=x^2$

are different functions even though they have the same behaviour!

Injective functions

Function $f : S → T$ is called an injection or 1-1 (one-to-one) if it satisfies (Inj)

Examples

functions that are injective

$f : N→N$ with $f(x) → x$

set complement (for a fixed universe)

functions that are not injective

absolute value, floor, ceiling

length of a word

Surjective functions

Function $f : S → T$ is called a surjection or onto if it satisfies (Sur). That is, if

$$Im(f ) = Codom(f)$$

Examples

functions that are surjective

$f : \mathbb{N} → \mathbb{N} \quad with \quad f(x) → x$

Floor, ceiling

functions that are not surjective

$f : \mathbb{N} → \mathbb{N} \quad with \quad f(x) → x^2$

$$f : \{a,...,e\}^∗ → \{a,...,e\}^∗ \quad with \quad f(w) → awe$$

Bijection functions

Both (Inj) and (Suj) functions

Functions on finite sets

Take Notice

For a finite set S and $f : S → S$ the properties surjective and injective are equivalent.

Functional Composition

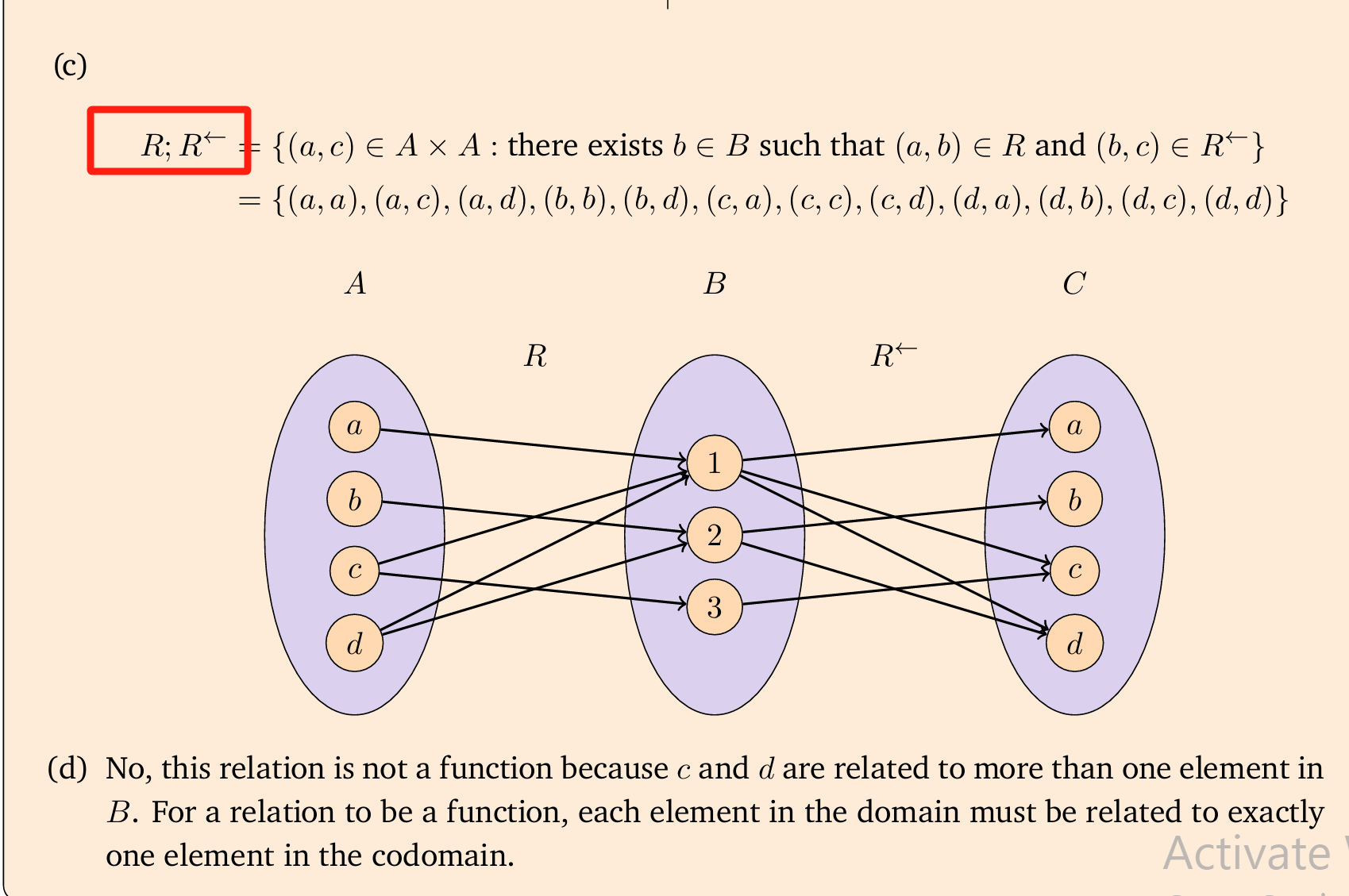
Q: If $f : S →T$ and $g :T →U$ are functions, then $f;g$ is a relation. When is it a function?

A: In the lecture, I said Injective. But Jiaojiao smiled and questioned ‘Is it sufficient?’. The correct answer is ‘Bijective’.

Definition

If $f : S →T$ and $g :T →U$ then the composition of f and g, written $g◦f$ , is the function given by

$$(g ◦ f)(x) = g(f(x))$$

That is, g ◦ f = f;g.

Take note of the order between f and g. f;g means f first and then g, and g ◦ f is the same of g(f(x)).

Facts

Composition is associative

h ◦(g ◦f) = (h◦g)◦f

For $g : S →T$ (note the g is different from the g above)

$$g ◦Id_S = g \quad and \quad Id_T ◦g =g$$

S->S->T and S->T->T

Iteration of Functions

If a function maps a set into itself, i.e. when Dom(f) = Codom(f), the function can be composed with itself — iterated

$$f ◦f,f ◦f ◦f,..., \text{ also written } f^2,f^3, \dots$$

exercise

Let $f ,g : \mathbb{Z} → \mathbb{Z}$ be given by $f(n) = n^2 +3$ and $g(n) = 5n−11$. What is:

$$f◦g(n) = (5n−11)^2 +3\\ g◦f(n) = 5(n^2+3)-11\\ g^2(n) = 5(5n-11)-11$$

Inverse Functions

Converse of a function

Q: If $f : S →T$, then $f^\leftarrow$ is a relation; when is it a function?

A: bijective

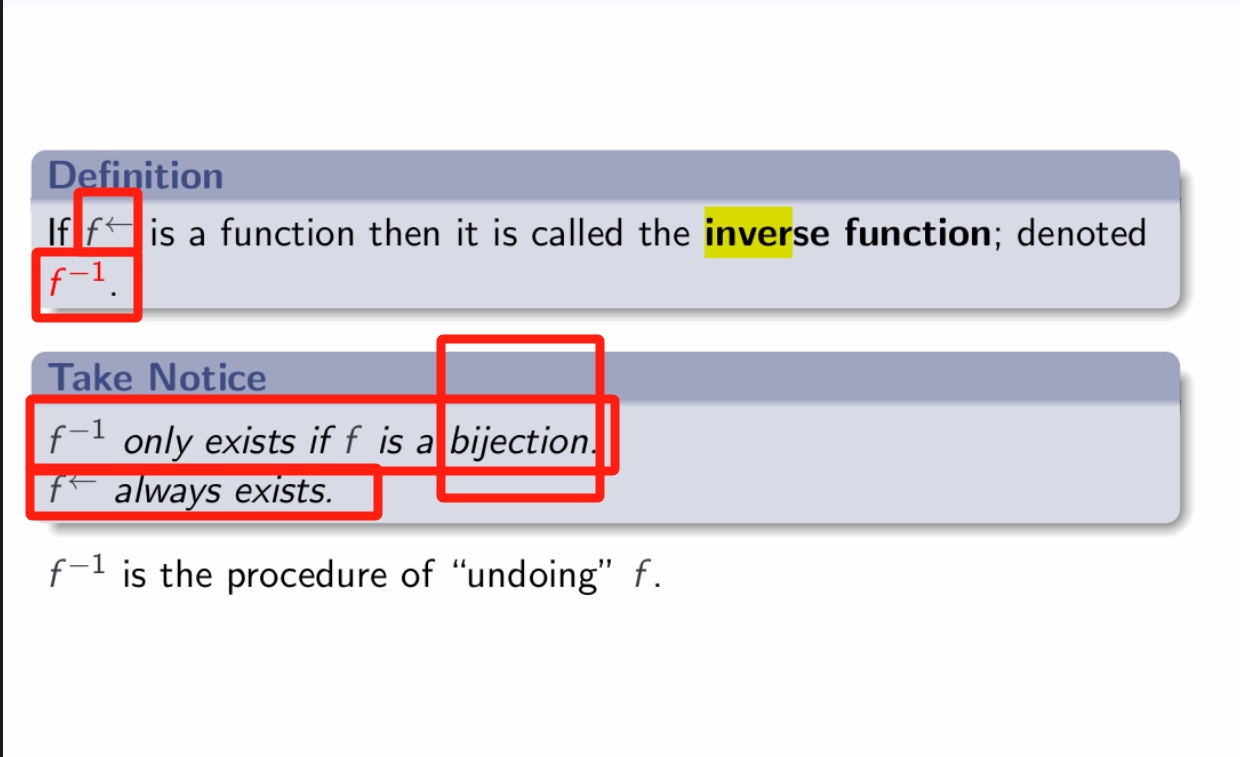
If $f^\leftarrow$ is a function then it is called the inverse function; denoted $f^{−1}$.

Take Notice

$f^{−1}$ only exists if f is a bijection.

$f^←$ always exists.

$f^{−1}$ is the procedure of “undoing” f .

Properties of the inverse

If $f : S →T$ and $f^{−1}$ exists then:

$$f^{−1} ◦f = Id_S \quad and \quad f◦f^{−1} =Id_T$$

Conversely, if $f : S → T \quad and \quad g : T → S$ and

$$g◦f =Id_S \quad and \quad f ◦g =Id_T$$

then $f^{−1}$ exists and is equal to g.

Exercises

Q:
f and g are ‘shift’ functions $\mathbb{N}→\mathbb{N}$ defined by f(n)=n+1, and g(n)=max(0,n−1)

(c) Is f injective? surjective?

A:
f(n)=n+1 (Inj) but 0 belongs to the co-domain, and f(n) cannot point 0, so it is not (Sur)

(d) Is g injective? surjective?

g(n)=max{0,n−1}, g(0)=g(1)=0, so g(n) is not (Inj), it is (Suj)

(e) Do f and g commute, i.e. ∀n((f◦g)(n) = (g◦f)(n))?

f(g(n))=g(n)+1=max{0, n-1}+1=max{1,n}, n belongs to Natural Number. The function’s result = 1 if n=0; =n if n>=1

g(f(n))=max{0,n+1-1}=max{0,n}

Thus f and g don’t commute.

---

Q:
Σ={a,b,c}

(c) Is length:$Σ^∗→\mathbb{N} \quad surjective$?

A:Yes, it is (Surj), $\lambda, a, aa, aaa, aaaa, \dots$.

(d) $length^←(2)\overset{?}{=}$

A:{aa,ab,ac,ba,bb,bc,ca,cb,cc}

---

Q:
Verifythat $f:\mathbb{R} \times \mathbb{R}→\mathbb{R} \times \mathbb{R}$ defined by $f(x,y)=(x+y,x−y)$ is invertible.

A: to prove the function is bijective.

$f(x,y)=(x+y,x−y) invertible \iff bijective (Inj)(Sur)$

$(Inj)$ suppose f(x,y)=(x+y,x−y),f(w,v)=(w+v,w−v)

$$\begin{cases} x+y=w+v \\ x−y=w−v \end{cases} \implies \begin{cases} 2x=2w \\ 2y=2v \end{cases} \implies (x,y)=(w,v)$$

$(Sur)$ for any $(m,n) \in \mathbb{R} \times \mathbb{R}$, we need to find (x,y), s.t. f(x,y)=(m,n)

f(x,y)=(x+y,x−y)=(m,n)

$$\implies \begin{cases} x+y=m \\ x−y=n \end{cases} \implies \begin{cases} 2x=m+n \\ 2y=m-n \end{cases} \implies \begin{cases} x=\frac{m+n}{2} \\ y=\frac{m-n}{2} \end{cases}$$

Matrices

An m×n matrix is a rectangular array with m horizontal rows and n vertical columns.

$$\begin{matrix} a_{11} & a_{12} & \dots & a_{13} \\ a_{21} & a_{22} & \dots & a_{23} \\ \vdots & \vdots & & \vdots \\\ a_{31} & a_{32} & \dots & a_{33} \end{matrix}$$

Take Notice

Matrices are important objects in Computer Science, e.g. for

• optimisation
• graphics and computer vision
• cryptography
• information retrieval and web search
• machine learning

Matrix Motivation

Solvinglinearequations:

5x=15

---

5x+3y = 15 and 4x−2y = 12

$$A = \left\{ \begin{matrix} 5 & 3 \\ 4 & 2 \\ \end{matrix} \right\}$$ $$x = \left\{ \begin{matrix} x\\ y\\ \end{matrix} \right\}$$ $$b = \left\{ \begin{matrix} 15\\ 12\\ \end{matrix} \right\}$$

hence

$$Ax=b$$

---

$$x' = 5x+3y \quad x'' = 2x'+y'\\ y' = 4x−2y \quad y'' = 3x'+3y'$$ $$A = \left\{ \begin{matrix} 5 & 3 \\ 4 & -2 \\ \end{matrix} \right\}$$ $$x = \left\{ \begin{matrix} x\\ y\\ \end{matrix} \right\}$$ $$x' = \left\{ \begin{matrix} x'\\ y'\\ \end{matrix} \right\}$$ $$B = \left\{ \begin{matrix} 2 & 1 \\ 3 & 3 \\ \end{matrix} \right\}$$ $$x'' = \left\{ \begin{matrix} x''\\ y''\\ \end{matrix} \right\}$$

Then how to simultaneous equations?

Basic Matrix Operations

The $transpose A^T$ of an $m \times n$ matrix $A = [a{ij}]$ is the $n \times m$ matrix whose entry in the ith row and jth column is $a{ji}$.

$$A= \begin{bmatrix} 2 & -1 & 0 & 4 \\ 3 & 2 & -1 & 2 \\ 4 & 0 & 1 & 3 \end{bmatrix}$$ $$A^T= \begin{bmatrix} 2 & 3 & 4 \\ -1 & 2 & 0 \\ 0 & -1 & 1 \\ 4 & 2 & 3 \\ \end{bmatrix}$$

Take notice

A matrix M is called symmetric if M^T = M

Matrix Sum

The sum of two $m \times n$ matrices $A = [a{ij}]$ and $B = [b{ij}]$ is the $m \times n$ matrix whose entry in the ith row and jth column is $a{ij} +b{ij}$.

$$A= \begin{bmatrix} 2 & -1 & 0 & 4 \\ 3 & 2 & -1 & 2 \\ 4 & 0 & 1 & 3 \end{bmatrix}$$ $$B= \begin{bmatrix} 1 & 0 & 5 & 3 \\ 2 & 3 & -2 & 1 \\ 4 & -2 & 0 & 2 \end{bmatrix}$$ $$A+B= \begin{bmatrix} 3 & -1 & 5 & 7 \\ 5 & 5 & -3 & 3 \\ 8 & -2 & 1 & 5 \end{bmatrix}$$

Fact:

$$A+B=B+A \quad and \quad (A+B)+C=A+(B+C)$$

Scalar Product

Given $m \times n$ matrix $A = [a{ij}]$ and $c ∈ \mathbb{R}$, the scalar product cA is the $m \times n$ matrix whose entry in the ith row and jth column is $c · a{ij}$.

$$A= \begin{bmatrix} 2 & -1 & 0 & 4 \\ 3 & 2 & -1 & 2 \\ 4 & 0 & 1 & 3 \end{bmatrix}$$ $$2A= \begin{bmatrix} 4 & -2 & 0 & 8 \\ 6 & 4 & -2 & 4 \\ 8 & 0 & 2 & 6 \end{bmatrix}$$

Matrix Product

The product of an $m \times n$ matrix $A = [a{ij}]$ and an n×p matrix $B=[b{jk}]$ is the $m \times p$ matrix $C = [c_{ik}]$ defined by

$$c_{ik} = \Sigma^n_{j=1} a_{ij}b_{jk} \quad for \quad 1 ≤ i ≤ m \quad and \quad 1≤k≤p$$ $$\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \cdot \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} = \begin{bmatrix} a_{11}b_{11}+a_{12}b_{21} & a_{11}b_{12}+a_{12}b_{22} \\ a_{21}b_{11}+a_{22}b_{21} & a_{21}b_{12}+a_{22}b_{22} \end{bmatrix}$$

Take Notice

The number of columns of A must be the same as the number of rows of B. (口诀“一行二列反相等”)

The product of a $1 \times n$ matrix and an $n \times 1$ matrix is usually called the inner product of two n-dimensional vectors. One line matrix multiples one column matrix, we could obtain only a number. Note, the 1 means only number 1, it is only a scalar, and n means 1-dimensional vector, just like.

$$\begin{bmatrix} a_{11} & a_{12} \end{bmatrix} \text{ to be the } 1 \times n$$

matrix,
and

$$\begin{bmatrix} b_{11}\\ b_{21} \end{bmatrix}$$

to be the $n \times 1$ matrix.

$$\begin{bmatrix} a_{11} & a_{21} \end{bmatrix}$$

to be the $1 \times n$ matrix.

Then

$$\begin{bmatrix} a_{11} & a_{12} \end{bmatrix}$$

$\cdot$

$$\begin{bmatrix} b_{11}\\ b_{21} \end{bmatrix}$$

= $a{11}b{11} + a{12}b{21}$

It is the inner product, which is also resulting in a scalar.

Consider

$$A= \begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}$$ $$B= \begin{bmatrix} 2 & -1 \\ -6 & 3 \end{bmatrix}$$

Calculate AB, BA

$$AB= \begin{bmatrix} -10 & 5 \\ -20 & 10 \end{bmatrix}$$ $$BA= \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}$$

Take Notice

In general, $A · B \neq B·A$

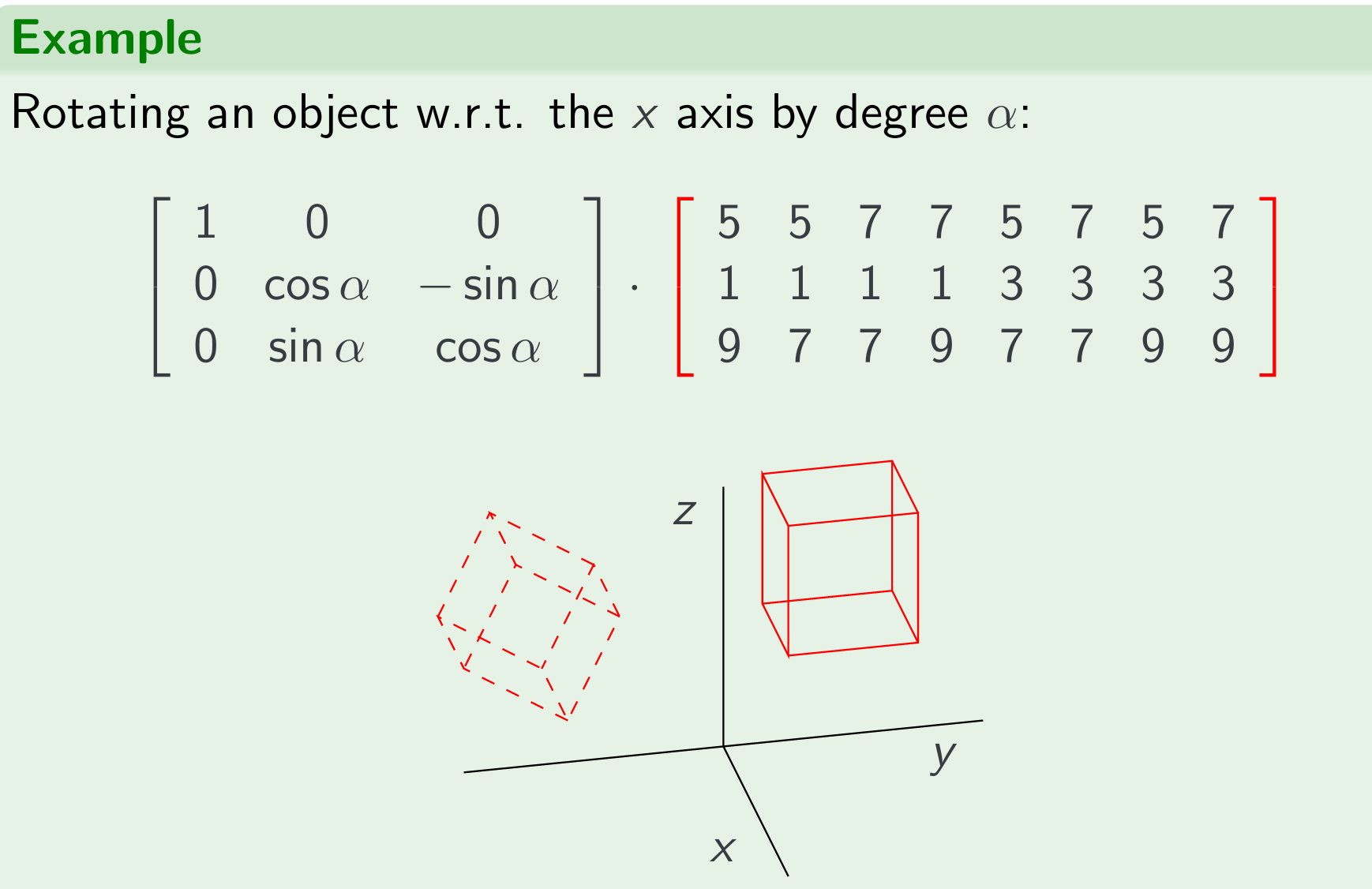
Computer Graphics

Rotating an object w.r.t. the x axis by degree α:

---

Introduction to Big-O Notation

Motivation

Want to compare functions, particularly functions from $\mathbb{N}$ to $\mathbb{R}$

Options

• Equality: $f(n) = g(n)$ for all n
• (Pointwise) comparison: $f(n) ≤ g(n)$ for all n
• (Almost all) comparison: $f(n) ≤ g(n)$ for all but finitely many n
• Asymptotic growth: $lim_{n->\infin} \frac{f(n)}{g(n)}$

example: Algorithmic analysis

Want to compare algorithms– particularly ones that can solve arbitrarily large instances.

We would like to be able to talk about the resources (running time, memory, energy consumption) required by a program/algorithm as a function f (n) of some parameter n (e.g. the size) of its input.

e.g. How long does a given sorting algorithm take to run on a listof n elements?

Issues

The exact resources required for an algorithm are difficult to pin down. Heavily dependent on:

• Environment the program is run in (hardware, choice of language, external factors, etc)

• Choice of inputs used

Cost functions can be complex, e.g.

$$2n log(n) + (n-100)log(n)^2 + \frac{1}{2^n} log(log(n))$$

Need to identify the “important” aspects of the function.

Look at the asymptotic growth: how do the costs scale as n gets large?

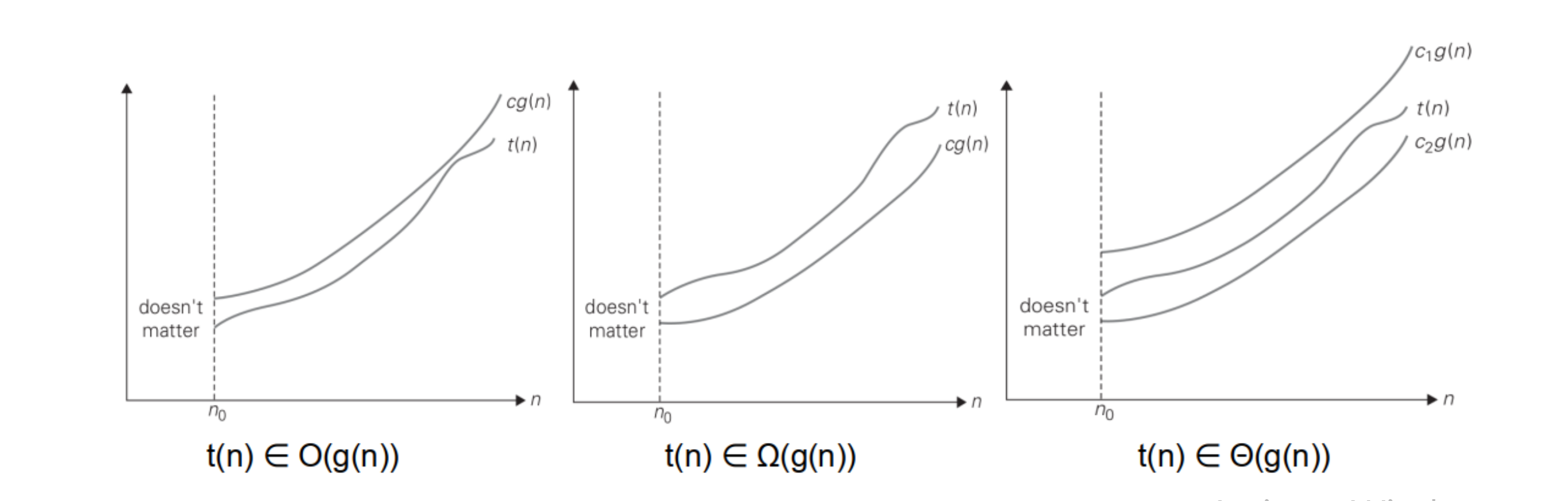
“Big-O” Asymptotic Upper Bounds

Definition:

Let $f,g:\mathbb{N} → \mathbb{R}_{≥0}$. We say that g is asymptotically less than f (or: f is an upper bound of g) if there exists $n_0 \in \mathbb{N}$ and a real constant $c > 0$ such that for all $n ≥ n_0$,

$$g(n) \leq c \cdot f(n)$$

Write O(f(n)) for the class of all functions g that are asymptotically less than f .

example

g(n) = 3n+1 ⇒ g(n)≤4n, for all n ≥1

Therefore, 3n + 1 ∈ O(n)

$$\frac{1}{10} n^2 \in O(n^2) \\ 10n log n \in O(n log n) \\ O(n log n) \nsubseteq O(n^2)$$

$O(n log n)$ is different from $O(n^2)$

Note! The traditional notation has been

g(n) = O(f(n))

instead of g(n) ∈ O(f(n)).

It allows one to use O(f(n)) or similar expressions as part of an equation; of course these ‘equations’ express only an approximate equality. Thus,

$$T(n) = 2·T(\frac{n}{2}) + O(n)$$

means “There exists a function $f (n) ∈ O(n)$ such that $T(n) = 2T(\frac{n}{2}) + f(n)$.”

properties

Suppose f (n) ∈ O(g(n)), g(n) ∈ O(h(n)) and j(n) ∈ O(k(n)).

Then:

• f(n) ∈ O(h(n))
• f(n) +j(n) ∈ O(g(n)+k(n))
• f(n) · j(n) ∈ O(g(n) · k(n))

example

$$5n^2 +3 n+2 ∈ O(n^2)\\ n^3 +2^{100}n^2 +2n +2^{2^{100}} ∈ O(n^3)$$

Generally, for constants $a_k … a_0$,

$$a_kn^k + a_{k-1}n^{k-1} + \dots + a_0 \in O(n^k)$$

“Big-Omega” Asymptotic Lower Bounds

Definition

Let $f,g : \mathbb{N} → \mathbb{R}$. We say that g is asymptotically greater than f (or: f is an lower bound of g) if there exists $n_0 ∈ \mathbb{N}$ and a real constant c > 0 such that for all $n ≥ n_0$

$$g(n) ≥ c ·f(n)$$

Write $\Omega(f(n))$ for the class of all functions g that are asymptotically greater than f.

Example

g(n) = 3n+1 ⇒ g(n)≥3n, for all n ≥1

Therefore, 3n + 1 ∈ Ω(n)

“Big-Theta” Notation

Definition

Two functions f,g have the same order of growth, or are asymptotically equivalent, if they scale up in the same way:
There exists $n_0 ∈ \mathbb{N}$ and real constants c > 0, d > 0 such that for all $n ≥ n_0$,

$$c · f (n) ≤ g(n) ≤ d ·f(n)$$

Write Θ(f(n)) for the class of all functions g that have the same order of growth as f .

If g ∈ O(f) (or Ω(f)) we say that f is an upper bound (lower bound) on the order of growth of g; if g ∈ Θ(f) we call it a tight bound.

Properties

Observe that, somewhat symmetrically

g∈Θ(f) ⇐⇒ f ∈Θ(g)

We obviously have

Θ(f(n)) ⊆ O(f(n)) and Θ(f(n)) ⊆ Ω(f(n)),

in fact

Θ(f(n)) = O(f(n)) ∩ Ω(f(n)).

At the same time the ‘Big-Oh’ is not a symmetric relation

g ∈O(f) ̸⇒ f ∈O(g),

but

g ∈O(f) ⇔f ∈Ω(g)

Observations

For all k,ϵ > 0:

$$O((log n)^k) ⊊ O(n^ϵ) \quad and \quad O(n^k) ⊊ O((1+ϵ)^n).$$

All logarithms have the same order, irrespective of base:

$$O(log_2 n) = O(log_3n) = ... = O(log_{10}n) = ...$$

Exponentials to different bases have different orders:

$$O(r^n) ⊊ O(s^n) ⊊ O(t^n) ... \quad for \quad r < s < t...$$

Similarly for polynomials

$$O(n^k) ⊊ O(n^l) ⊊ O(n^m) ... \quad for \quad k < l < m...$$

Examples

Here are some of the most common functions occurring in the analysis of the performance of programs (algorithm complexity), arranged in increasing asymptotic growth:

$$1, log log n, log n, √n, √n(log n), n, n(log log n), nlogn,n√n, n^2, n^2 logn, n^3, n^{12}, 2^{√n}, 1.01^n, 2^n, 3^n, n!, n^n, 2^{n^2},...$$

Take Notice

$O(1) ≡ const$, although technically it could be any function that varies between two constants c and d.

Exercises

Q: True or false?

$$(a) 2^{n+1}∈O(2^n) \\ (b) (n+1)^2 ∈ O(n^2) \\ (c) 2^{2n} ∈ O(2^n) \\ (d) (200n)^2 ∈ O(n^2) \\ (b) log(n^{73})∈O(log n) \\ (c) log(n^n) ∈ O(log n) \\ (d) (√n+1)^4 ∈ O(n^2)$$

A:
TTF->$O(4^n)$
TTFT

---

Welcome to point out the mistakes and faults!