PREFACE

• What is logic
  • Loose history of logic
  • Logic in Computer Science
• Boolean Logic
  • The Boolean Algebra $\mathbb{B}$
  • Alternative notation
  • Alternative notation
  • Properties:Commutativity,Associativity,Distribution,Identity,Complementation
• Boolean Functions
  • example
  • Application: Adding two one-bit numbers
• Conjunctive and Disjunctive Normal Form
  • Examples
  • 2 Theorems
• Canonical DNF
  • Theorem
  • Exercise
• Karnaugh Maps
  • proof process of Karnaugh Maps (K Maps for short)
  • Why, how to use Karnaugh Maps
  • how to correctly circle to eliminate variables?
  • example
  • Exercise
• Boolean Algebras
  • definition
  • property
  • Example
  • Proofs in Boolean Algebras
  • Duality
    • Definition
    • Definition
    • Theorem (Principle of duality)
    • Example

What is logic

Logic is about formalizing reasoning and defining truth

• Adding rigour
• Removing ambiguity
• Mechanizing the process of reasoning

Loose history of logic

(Ancient times): Logic exclusive to philosophy
Mid-19th Century: Logical foundations of Mathematics (Boole, Jevons, Schr¨oder, etc)
1910: Russell and Whitehead’s Principia Mathematica
1928: Hilbert proposes Entscheidungsproblem
1931: G¨odel’s Incompleteness Theorem
1935: Church’s Lambda calculus
1936: Turing’s Machine-based approach
1930s: Shannon develops Circuit logic
1960s: Formal verification; Relational databases

Logic in Computer Science

Computation = Calculation + Symbolic manipulation

Logic as 2-valued computation (Boolean logic):

• Circuit design
• Code optimization
• Boolean algebra
• Nand game

Logic as symbolic reasoning (Propositional logic, and beyond):

• Formal verification
• Proof assistance
• Knowledge Representation and Reasoning
• Automated reasoning
• Databases

Boolean Logic

Boolean logic is about performing calculations in a “simple” mathematical structure.

• complex calculations can be built entirely from these simple ones
• can help identify simplifications that improve performance at the circuit level
• can help identify simplifications that improve presentation at the programming level

The Boolean Algebra $\mathbb{B}$

Definition

The (two-element) Boolean algebra is defined to be the set $\mathbb{B}$ ={0,1}, together with the functions

$$!: \mathbb{B} \to \mathbb{B}, \&\&: \mathbb{B}^2 → \mathbb{B}, \quad and \quad ||: \mathbb{B}^2 → \mathbb{B}$$

, defined as follows:

$$!x = (1−x) \\ x \&\&y =min\{x,y\} \\ x ∥ y =max\{x,y\}$$

Alternative notation

For $\mathbb{B}$

$$\mathbb{B} = \{ \text{false}, \text{true} \} \quad \text{or} \quad \mathbb{B} = \{ F, T \} \quad \text{or} \quad \mathbb{B} = \{ 0, 1 \} \quad \text{or} \quad \mathbb{B} = \{ \bot, \top \}$$

For $!x$

$$\overline{x} \quad !x \quad \text{or} \quad x' \quad \text{or} \quad \sim x \quad \text{or} \quad \neg x \quad \text{or} \quad \text{NOT}(x)$$

For $x \&\& y$

$$x \land y \quad \text{or} \quad xy \quad \text{or} \quad x \wedge y \quad \text{or} \quad (x \, \text{AND} \, y)$$

For $x || y$

$$x \lor y \quad \text{or} \quad x + y \quad \text{or} \quad (x \, \text{OR} \, y)$$

Alternative notation

Definition

The (two-element) Boolean algebra is defined to be the set $\mathbb{B}$ ={false,true}, together with the functions $! :\mathbb{B} \to \mathbb{B}, \&\&: B^2 →B, and \quad ∥: B^2 →B$, defined as follows:

x	!x
false	true
true	false

---

x	y	x&&y
false	false	false
false	true	false
true	false	false
true	true	true

---

x	y	x or y
false	false	false
false	true	true
true	false	true
true	true	true

Properties:Commutativity,Associativity,Distribution,Identity,Complementation

We observe that !, &&, and ∥ satisfy the following:

For all $x,y,z ∈ \mathbb{B}$:

Commutativity

$$x ∥ y =y ∥x \\ x \&\&y =y \&\& x$$

Associativity

$$(x ∥ y) ∥ z =x ∥(y ∥z) \\ (x \&\& y) \&\&z =x \&\&(y \&\& z)$$

Distribution

$$x ∥ (y \&\&z) =(x ∥y)\&\&(x ∥ z) \\ x \&\&(y ∥z) =(x \&\& y)∥(x \&\& z)$$

Identity

$$x ∥ 0=x \\ x \&\& 1=x$$

Complementation

$$x ∥ (!x) = 1 \\ x \&\&(!x) = 0$$

Boolean Functions

Definition

An n-ary Boolean function is a map f : $\mathbb{B}^n \to \mathbb{B}$.

Q: How many unary Boolean functions are there? How many binary functions? N-ary?

$\mathbb{B}^2 \to \mathbb{B}$, we found there are 4 possible inputs and 2 possible outputs of each input, so here is $2222=16$ *possible outputs.

Note, the question didnot mention the specific function, so don’t think 0,0->0 directly, cause maybe 0,0->1 function. Additionally, the different outputs should multiple as possible results. Just regard different combination of the outputs as a new function.

4 means how many input here.

How many unary Boolean functions are there? n-ary?

unary means One-dimensional relation. So how many, it’s 2+2=4 obviously.

$$2^{2^{2}}=4$$

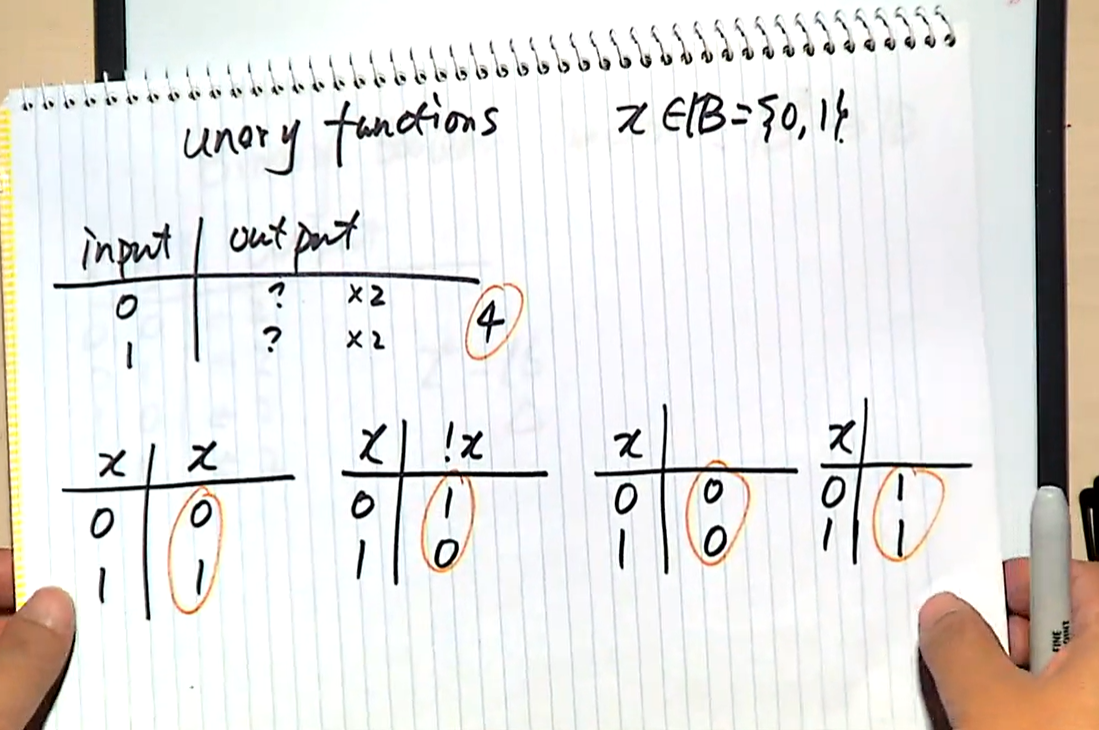
So n-ary is:

$$2^{2^{n}}=$$

example

$!$ is a unary Boolean function

$\&\&, ∥$ are binary Boolean functions

$f(x,y) =!(x \&\& y)$ is a binary boolean function (NAND)

$And(x_0,x_1,…) = (···((x_0 \&\& x_1) \&\& x_2)···)$ is a (family) of Boolean functions

$Or(x_0,x_1,…) = (···((x_0 ∥ x_1) ∥ x_2)···)$ is a (family) of Boolean functions

Application: Adding two one-bit numbers

Question. How can we implement:

$add: \mathbb{B}^2 \to \mathbb{B}^2$

defined as

x	y	add(x,y)
0	0	00
0	1	01
1	0	01
1	1	10

Take Notice

Observe that this is not a Boolean function. Boolean functions can output either 0 or 1 (a single bit). This function outputs 2 bits.

(Short) Answer. Use two Boolean functions!

Take Notice

Digital circuits are just sequences of Boolean functions.

Conjunctive and Disjunctive Normal Form

Definition

A literal is a unary Boolean function

A minterm is a Boolean function of the form $And(l_1(x_1),l_2(x_2),…,l_n(x_n))$ where the $l_i$ are literals

A maxterm is a Boolean function of the form $Or(l_1(x_1),l_2(x_2),…,l_n(x_n))$ where the $l_i$ are literals

A CNF Boolean function is a function of the form $And(m_1,m_2, …)$, where the $m_i$ are maxterms.

A DNF Boolean function is a function of the form $Or(m_1,m_2, …)$, where the $m_i$ are minterms.

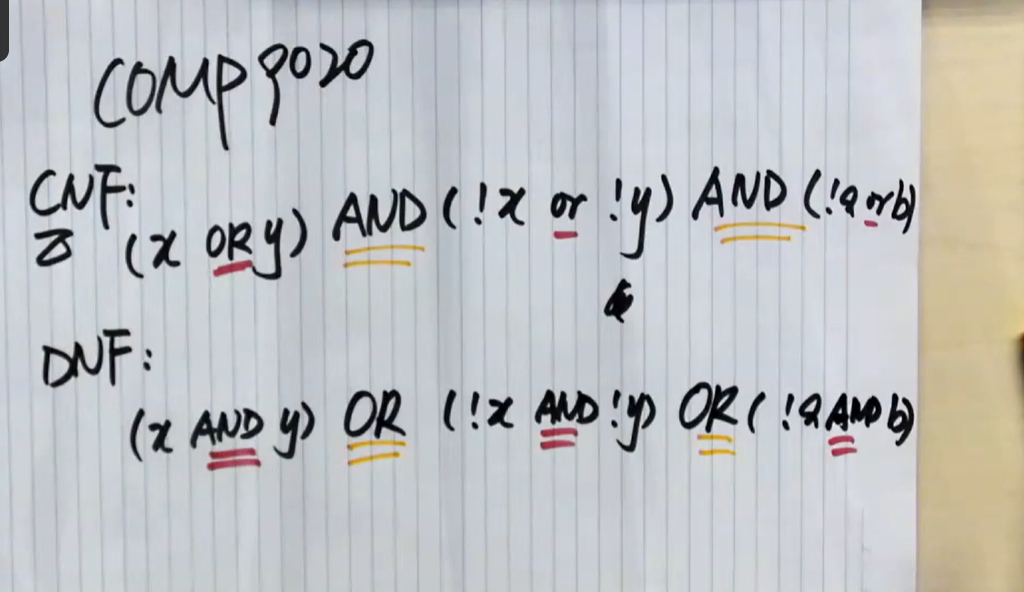
Take Notice

CNF: product of sums; DNF: sum of products

秘笈：“C与D或”,“C与小D或大”，“min AND, max OR, C与积，D或和”

Examples

Question. Are these functions in CNF? Are they in DNF?

$$f(x,y,z) = (x \&\& (!y) \&\& z) ∥ (x \&\& (!y) \&\& (!z)) = x \overline{y} z +x \overline{y} \overline{z}$$

DNF , but not CNF

$$g(x,y,z) = (x ∥ (!y) ∥ z) \&\& (x ∥ (!y) ∥ (!z)) = (x +\overline{y} +z)(x +\overline{y} +\overline{z} )$$

CNF function, but not DNF

$$h(x,y,z) = (x \&\& (!y) \&\& z) = x \overline{y} z$$

both CNF and DNF

Note! Paul Hunter (lecturor):

Note: CNF/DNF/minterms/maxterms are only concerned with  how the formula appears as written.  You cannot "change" the formula (e.g. "x can be regarded as x or x") and have things be meaningful.

(x && !y) && z is:

A maxterm

An OR of maxterms: because OR(m) = m, so it is equal to OR((x&&!y)&&z) - therefore it is in DNF

An AND of minterms: because x is a minterm, !y is a minterm, and z is a minterm, so it is equal to AND(x, !y, z) - therefore it is in CNF

Leo Liu:
I'm still confused, why x, !y and z are miniterms? Because x = AND(x)? So x can be considered as literal (x), miniterm (AND(x)), and maxterm (OR(x))? 

Paul Hunter:
Yes, that's correct.

AND and OR are "generalizations" of && and ||.

&& and || are functions that take two inputs, AND and OR are (families of) functions that take arbitrarily many inputs.

My thought:

$$j(x, y,z) = x +y(z +x)$$

Neither CNF nor DNF

2 Theorems

Every Boolean function can be written as a function in DNF.

Every Boolean function can be written as a function in CNF.

Canonical DNF

Given an n-ary Boolean function $f: \mathbb{B}^n \to \mathbb{B}$ we construct an equivalent DNF Boolean function as follows:

For each $b = (b_1, \dots, b_n) \in \mathbb{B}^n$ we define the minterm

Note, $\mathbb{B}^n$ means $\mathbb{B} \times \mathbb{B} \times \mathbb{B} \times \dots$, so $b = (b_1, \dots, b_n)$ is a product (AND) of them, and the product means minterm.

$$m_b = AND(l_1(x_1),l_2(x_2), \dots,l_n(x_n))$$

where

$$l_i(x_i)= \begin{cases} x_i \quad if \quad b_i = 1\\ !x_i \quad if \quad b_i = 0 \end{cases}$$

We then define the DNF formula:

$$f_{DNF} = \sum\limits_{f(b)=1}^{} m_b$$

that is, $f_{DNF}$ is the disjunction (or) over all minterms corresponding to elements $b ∈ \mathbb{B}$ where $f(b) = 1$.

Note, $m_b$ is the each expression of $l_i(x_i)$. Cause we want to build a DNF, so the external operation is AND().

Note to distinguish the opposite operations. Firstly, $+$ and $\times$; Secondly, $AND()$(CNF,$\times$) and $OR()$(DNF,$+$).

“C与D或，与乘或加”

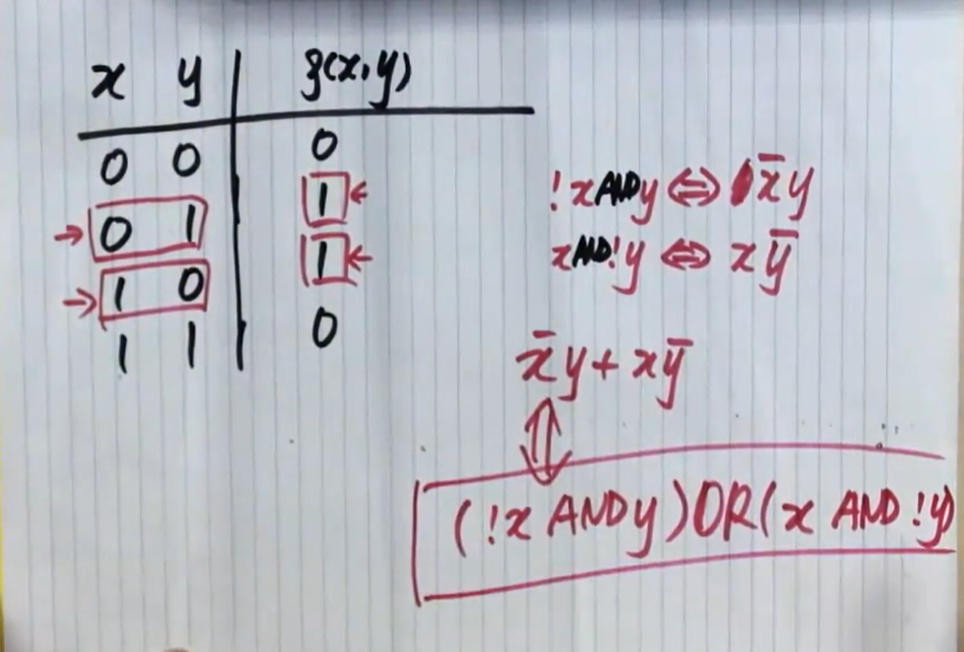
Theorem

f and $f_{DNF}$ are the same function.

Exercise

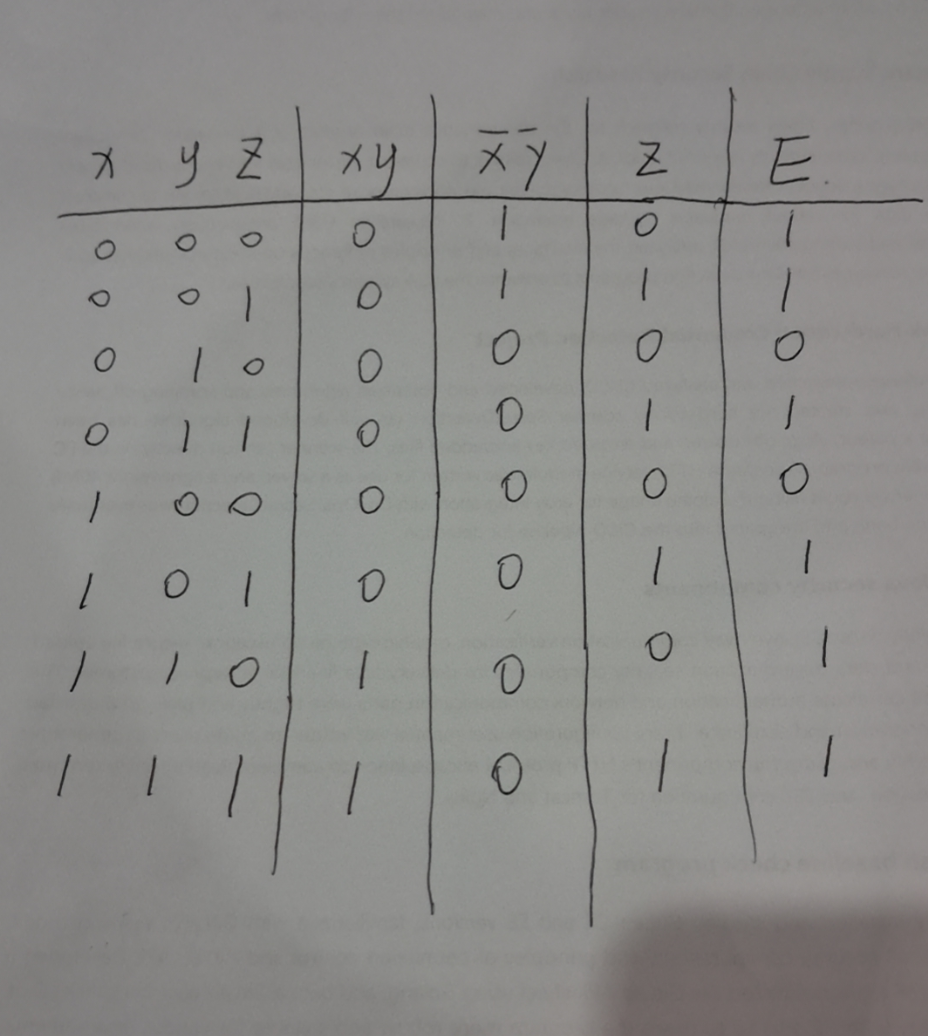
Find the canonical DNF form of each of the following expressions in variables x,y,z

• $xy$
• $\overline{z}$
• $xy + \overline{z}$
• $f(x,y,z)=1$

Note Jiaojiao’s handwriting below, the addtional expressions with different colors are the corresponding answers.

Karnaugh Maps

Jiaojiao remark:”Not very useful.”

For up to four variables (propositional symbols) a diagrammatic method of simplification called Karnaugh maps works quite well.

• For every propositional function of k = 2,3,4 variables we construct a rectangular array of $2^k$ cells.
• Column labels and row labels are ordered by Gray code.
• Squares corresponding to the value true are marked with eg “+”.
• We try to cover these squares with as few rectangles with sides 1 or 2 or 4 as possible.

proof process of Karnaugh Maps (K Maps for short)

The section would be in Chinese… just for next quiz of Data Structure.

卡诺图只是为了获取一个随机DNF的方法。

首先需要找到变量 w,x,y,z,然后我们还知道 f(w, x, y, z), 我们先做一个真值表(Truth table),然后我们让f(w, x, y, z)是随机的0或1.

如下图，右侧真值表，得到左侧卡诺图，这是我们的题目，我们在随机真值的cell中打’+’

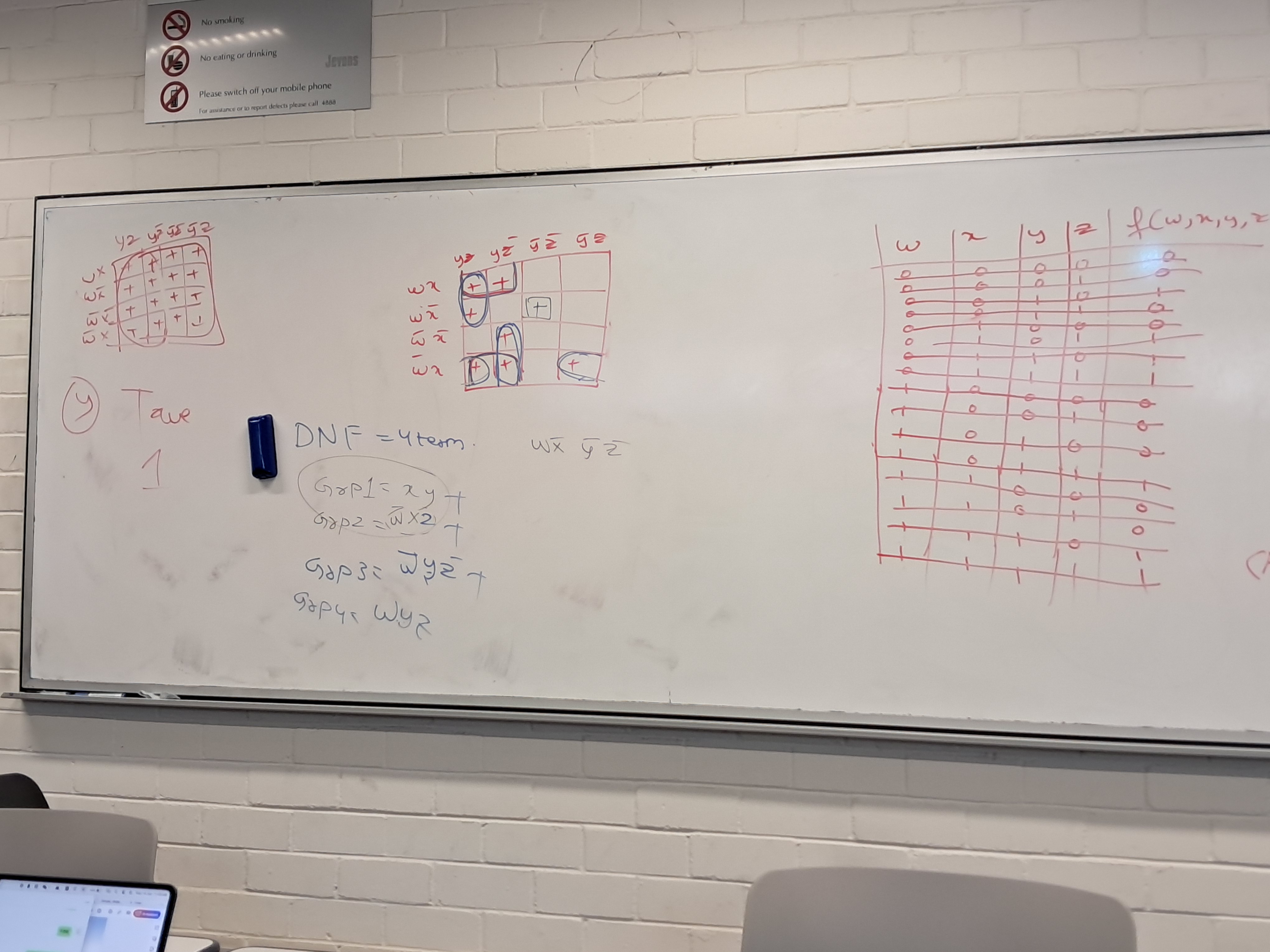
画卡诺图，比如4变量，就画4x4=16的table，如果是3变量，就画3x3=9的table。

注意table的title，行列的title一次只变一个。比如，wx->w!x->!w!x->!wx, 不要一下子wx->!w!x，这样会错。

Why, how to use Karnaugh Maps

接下来说卡诺图能解决的问题，主要就是为了消除单个minterm的无关变量，获得DNF的所有minterms。

圈的时候，从最大往最小圈，记得每行每列首位相连。如图，左下侧俩和左上侧俩是最大的，因为一下子占2x2的方的四个cells，所以先圈他俩。

然后开始往小圈，全部的+都被圈完后，就可以得到minterms。

比如图中，有个孤零零的w!x!y!z，肯定是最后圈，可惜消不了任何变量，因此这个minterm就是w!x!y!z。

how to correctly circle to eliminate variables?

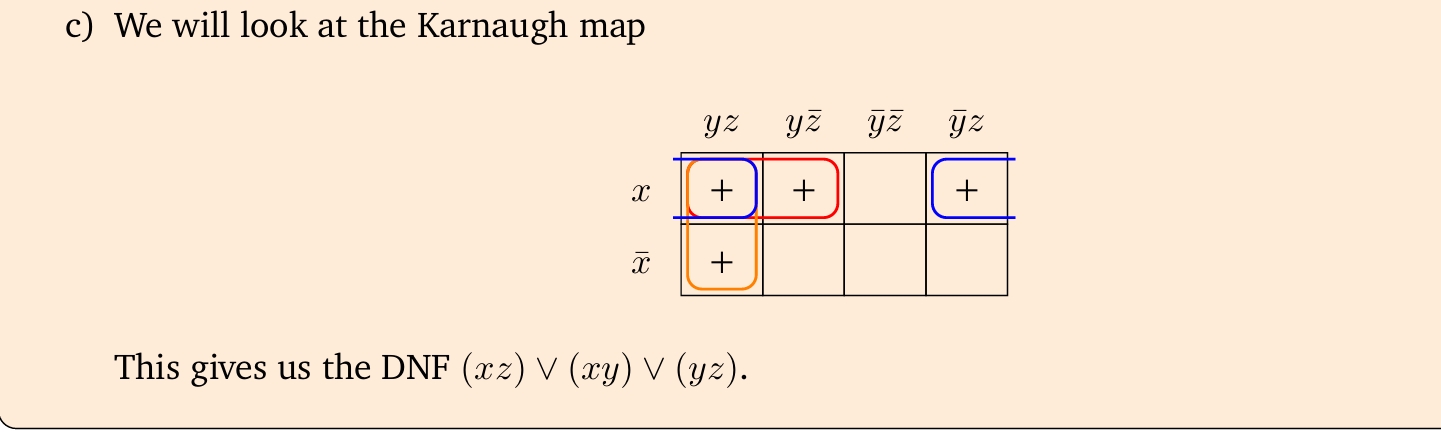
In the pic of the sample before mid-term test, it is wrong. Because it is not $n \times m$ cells with full $+$.

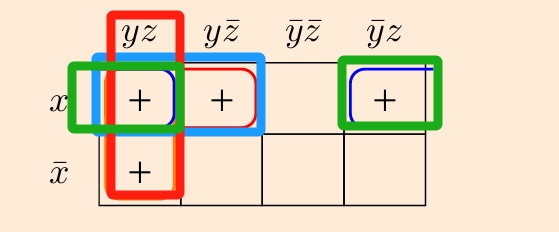
Follow me, it is the correct way to circle them. We must circle $n \times m$ cells with fully $+$.

blue:xy

green: xz

red: yz

example

Note, the Karnaugh Map is at the first, and then we got the Expression. Don’t confuse the order of the pic and the expression.

Use $2^n$ to circle the cells, and cover all the true cells.

$$E = (xy) \lor (\overline{x} \overline{y}) \lor (z)$$

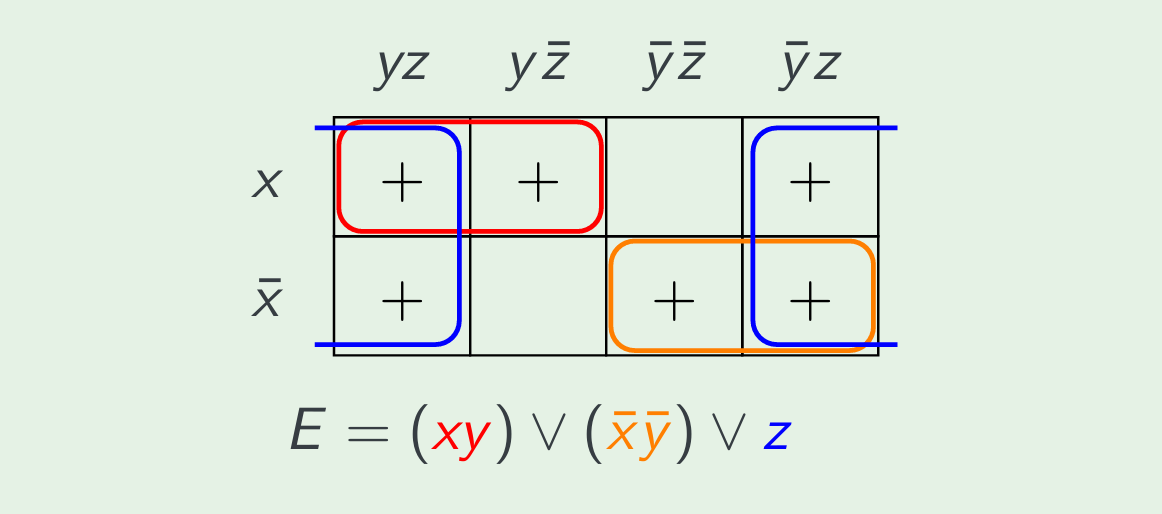
Canonical form would consist of writing all cells separately (6 clauses).

For optimisation, the idea is to cover the + squares with the minimum number of rectangles. One cannot cover any empty cells.

• The rectangles can go ‘around the corner’/the actual map should be seen as a torus.
• Rectangles must have sides of 1, 2 or 4 squares (three adjacent cells are useless).

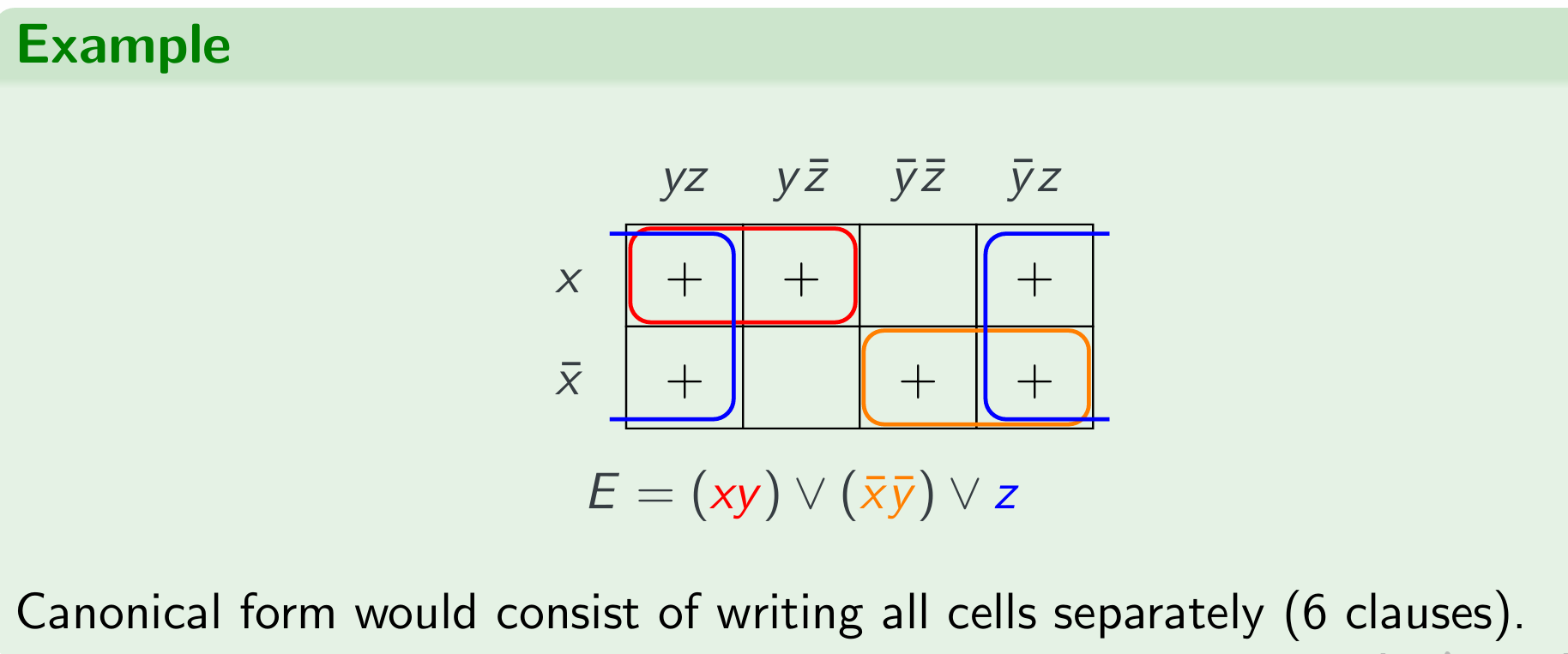
Of course it is similar to the manual calcute the 0 and 1.

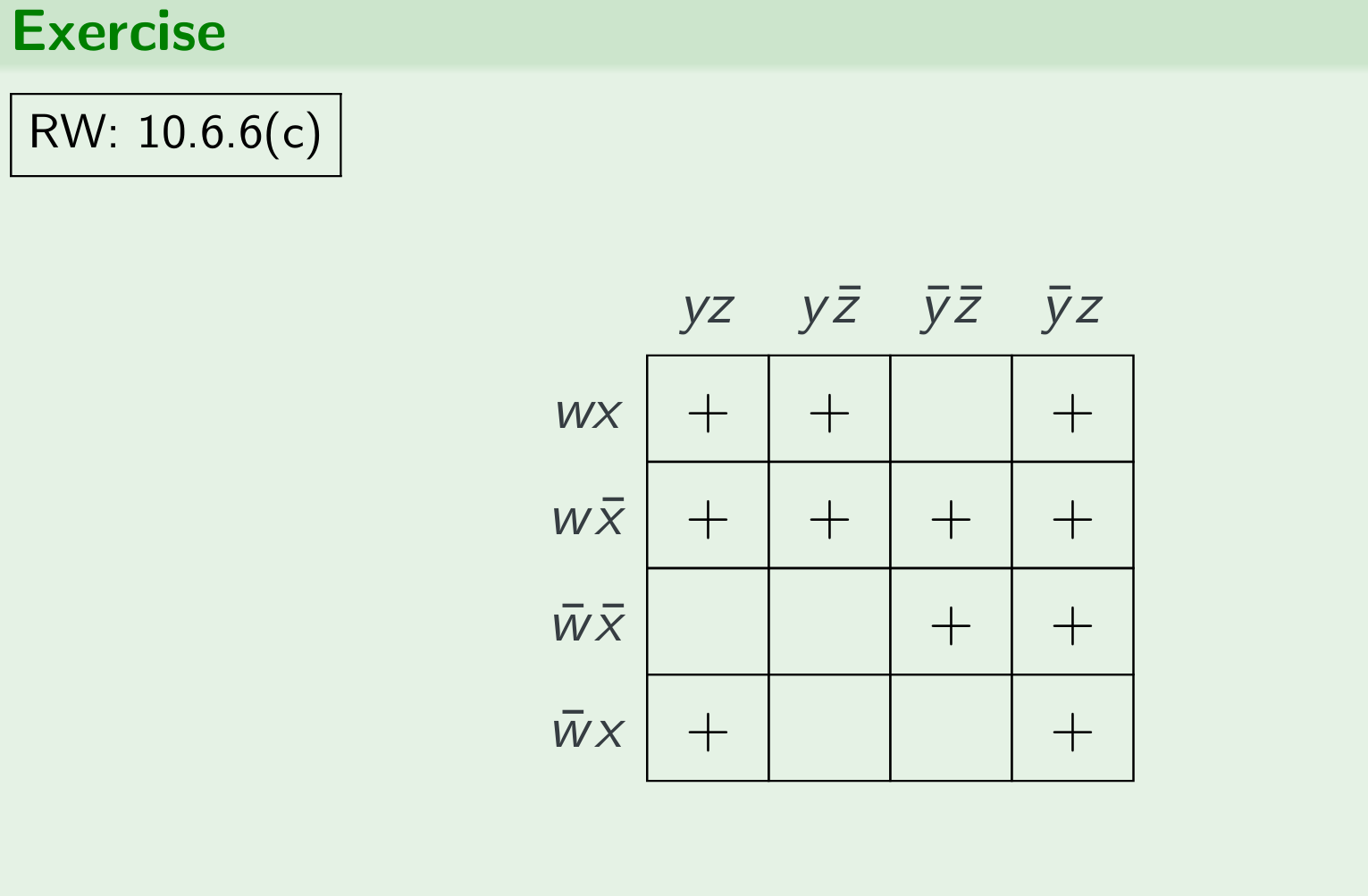
Exercise

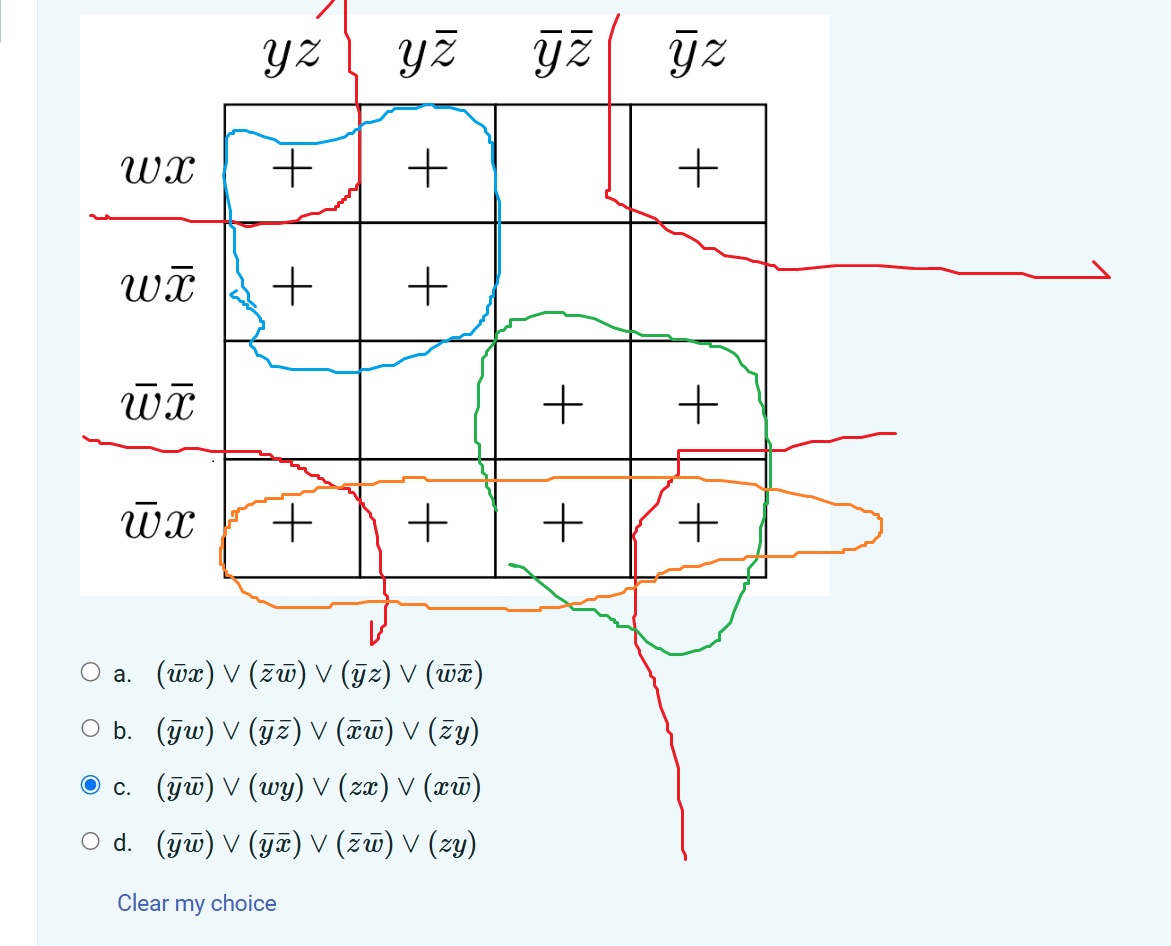
The Karnaught Map just generate the expression rapidly.

Boolean Algebras

definition

A Boolean algebra is a structure $(T, \lor, \land, ‘, 0, 1)$ where

• 0, 1 ∈ T
• ∨,∧ : T ×T →T (called join and meet respectively)
• ′ : T→T (called complementation)

property

and the following laws hold for all x,y,z ∈ T:

Commutativity:

$$x ∨y =y ∨x, x∧y =y∧x$$

Associativity:

$$(x ∨y)∨z =x ∨(y ∨z)\\ (x ∧y)∧z =x ∧(y ∧z)$$

Distributivity:

$$x ∨(y ∧z) =(x ∨y)∧(x ∨z) \\ x ∧(y ∨z) =(x ∧y)∨(x ∧z)$$

Identity:

$$x ∨0=x, x∧1=x$$

Complementation:

$$x∨x' =1, x ∧x' =0$$

Example

The set of subsets of a (singleton) set X = {x}:

• T : Pow(X)={{x},∅}
• ∨ (join) : ∪
• ∧ (meet) : ∩
• ′ (complement) : $·^c$
• 0 : ∅
• 1 : $X \qquad (\mathbb{U})$

The Laws of Boolean algebra follow from the Laws of Set Operations.

---

The two element Boolean Algebra :

$$B =(\{true,false\},∥,\&\&,!,false,true)$$

where !,&&,∥ are defined as:

• !true = false; !false = true,
• true && true = true; …
• true ∥ true = true; …

---

Cartesian products of $\mathbb{B}$, that is n-tuples of 0’s and 1’s with Boolean operations, e.g. $\mathbb{B}^4$:

join: $(1,0,0,1) ∨ (1,1,0,0) = (1,1,0,1)$

meet: $(1,0,0,1) ∧ (1,1,0,0) = (1,0,0,0)$

complement: $(1,0,0,1)’ = (0,1,1,0)$

0 : $(0,0,0,0)$

1 : $(1,1,1,1)$

---

Functions from any set $S$ to $\mathbb{B}$; that is, $\mathbb{B}^S$

If $f,g:S \to \mathbb{B}$ then

$$(f ∨g) : S →B \quad defined by \quad s →f(s)∥g(s)$$ $$(f ∧g) : S →B \quad defined by \quad s →f(s)\&\&g(s)$$ $$f' : S →B \quad defined by \quad s→!f(s)$$ $$0 : S →B \quad is the function \quad s → 0$$ $$1 : S →B \quad is the function \quad s → 1$$

Proofs in Boolean Algebras

If you can show that an identity holds using the laws of Boolean Algebra, then that identity holds in all Boolean Algebras.

Example

Claim: In all Boolean Algebras

$$x ∧x =x \quad \text{for all } x ∈ T.$$

Proof:

$$x = \\ x∧1 \quad [Identity] \\ =x ∧(x ∨x') \quad [Complement] \\ =(x ∧x)∨(x ∧x') \quad [Distributivity] \\ =(x ∧x)∨0 \quad [Complement] \\ =(x ∧x) \quad [Identity]$$

Duality

Definition

If $E$ is an expression defined using variables $(x, y, z, etc)$, constants $(0 and 1)$, and the operations of Boolean Algebra $(∧, ∨, and ‘)$ then $dual(E)$ is the expression obtained by replacing $∧$ with $∨$ (and vice-versa) and $0$ with $1$ (and vice-versa).

Definition

If $(T,∨,∧, ‘,0,1)$ is a Boolean Algebra, then $(T,∧,∨, ‘,1,0)$ is also a Boolean algebra, known as the dual Boolean algebra.

(Dual means the contray operation and element: ∨->∧; ∧->∨; 0->1; 1->0; )

Theorem (Principle of duality)

If you can show $E_1 = E_2$ using the laws of Boolean Algebra, then $dual(E_1) = dual(E_2)$.

Example

We have shown $x ∧x = x$.

By duality: $x ∨ x = x$.

---

Welcome to point out the mistakes and faults!