Propositional Logic

Math

Created At : 2024-10-15 07:00

Count:3.4k Views 👀 :

Comment:

Propositional Logic, informally
Propositional Logic, formally
CNF and DNF Revisited
Beyond Propositional Logic

Propositional Logic, informally
Propositional Logic, formally
CNF and DNF Revisited
Beyond Propositional Logic

Propositional Logic, informally

A proposition (or sentence) is a declarative statement; something that is either true or false.

Examples

Richard Nixon was president of Ecuador.
A square root of 16 is 4.
Euclid’s program gets stuck in an infinite loop if you input 0.
$x^n +y^n =z^n$ has no nontrivial integer solutions for n > 2.
3 divides 24.
K_5 is planar.

The following are not declarative sentences:

Gubble gimble goo
For Pete’s sake, take out the garbage!
Did you watch MediaWatch last week?
Please waive the prerequisites for this subject for me.
x divides y. — R(x,y)
x =3 and x divides 24. — P(x)

Logical connectives

Logical connectives join together propositions to build larger, compound propositions.

Examples

Chef is a bit of a Romeo and Kenny is always getting killed.
Either Bill is a liar or Hillary is innocent of Whitewater.
It is not the case that this program always halts.
If it is raining then I have an umbrella.

Logical connectives

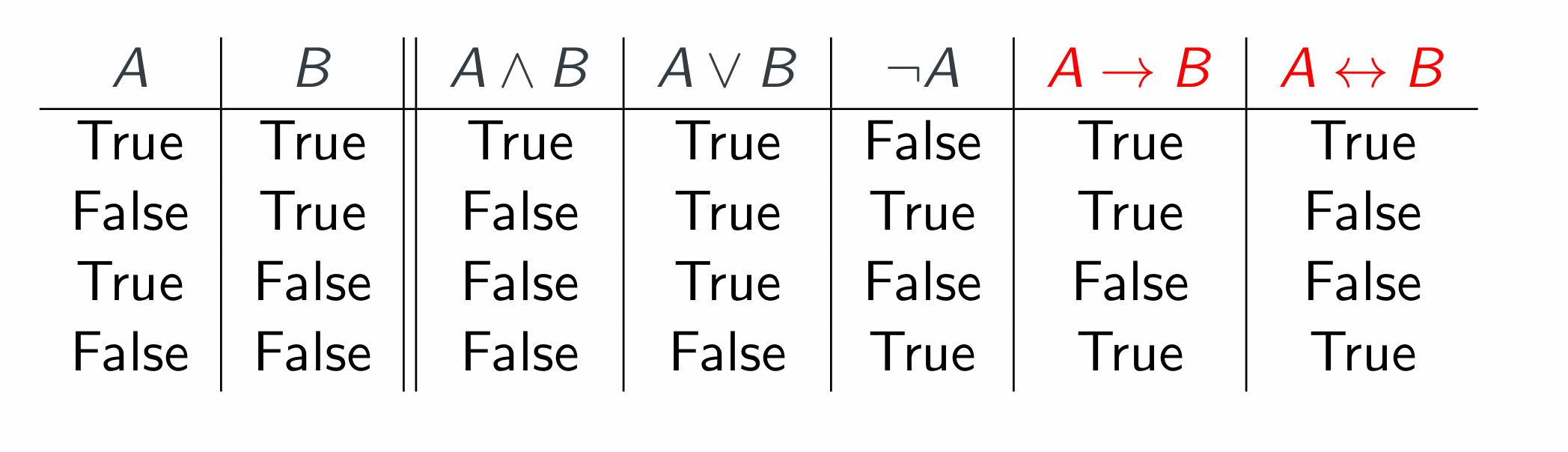
Common logical connectives:

Symbol	Default	Also known as
∧	and	but,“;”
∨	or	“either .. or ..”
¬	not	not the case
→	“if .. then..”	implies, whenever, is sufficient for
↔	“.. ifandonlyif ..”	bi-implies, necessary and sufficient, exactly when, just in case

Compound propositions

The truth of a compound proposition depends on the truth of its components (atomic propositions):

example

P: Chef is a bit of a Romeo and Kenny is always getting killed.

Chef is a bit of a Romeo	Kenny is always getting killed	P
True	True	True
False	True	False
True	False	False
False	False	False

Vacuous truth

Interesting! I thought the topic in my former article 由空集和子集，想到空洞真理.

How to interpret A → B when A is false?

A→B If A(premise) then B (conclusion)

Material implication is false only when the premise holds and the conclusion does not.

If the premise is false, the implication is true no matter how absurd the conclusion is.

Both the following statements are true:

If February has 30 days then March has 31 days.
If February has 30 days then March has 42 days.

Exercises

p = “youget an HD on your final exam”

q = “youdoevery exercise in the book”

r = “you get an HD in the course”

Translate into logical notation:

(a) You get an HD in the course although you do not do every exercise in the book.

r∧¬q

r→p

(d) Youget an HDonyour exam, but you don’t do every exercise in this book; nevertheless, you get an HD in this course.

p∧¬q∧r

Tautologies, Contradictions and Contingencies

同义反复、矛盾和偶然性

Definition

A proposition is:

a tautology if it is always true,
a contradiction if it is always false,
a contingency if it is neither a tautology or a contradiction,
satisfiable if it is not a contradiction.

Example

Contingency: It is raining
Tautology: It is raining or it is not raining
Contradiction: It is raining and it is not raining

Applications I: Constraint Satisfaction Problems

These are problems such as timetabling, activity planning, etc.

Many can be understood as showing that a formula is satisfiable.

Example

You are planning a party, but your friends are a bit touchy about who will be there.

Sarah hates John’s jokes. She will not come to the party if John is invited.
Kim loves John’s jokes, and says she will not come unless John does.
Sarah is shy, and will only come to the party if her best friend Kim will be there.

Who can you invite without making someone unhappy?

Translation to logic: let J,S,K represent “John (Sarah, Kim) comes to the party”. Then the constraints are:

J →¬S
K →J
S →K

Thus, for a successful party to be possible, we want the formula $φ =(J →¬S)∧(S →K)∧(K →J)$ to be satisfiable. Truth values for J,S,K making this true are called satisfying assignments, or models.

We can use logical reasoning to work out what options are available:

If Kim comes, then John must, and Sarah must not.
If Kim doesn’t come, then Sarah cannot come. John may or may not come.

Conclusion: a party satisfying the constraints can be held. Invite nobody, or invite John only, or invite Kim and John.

Exercise

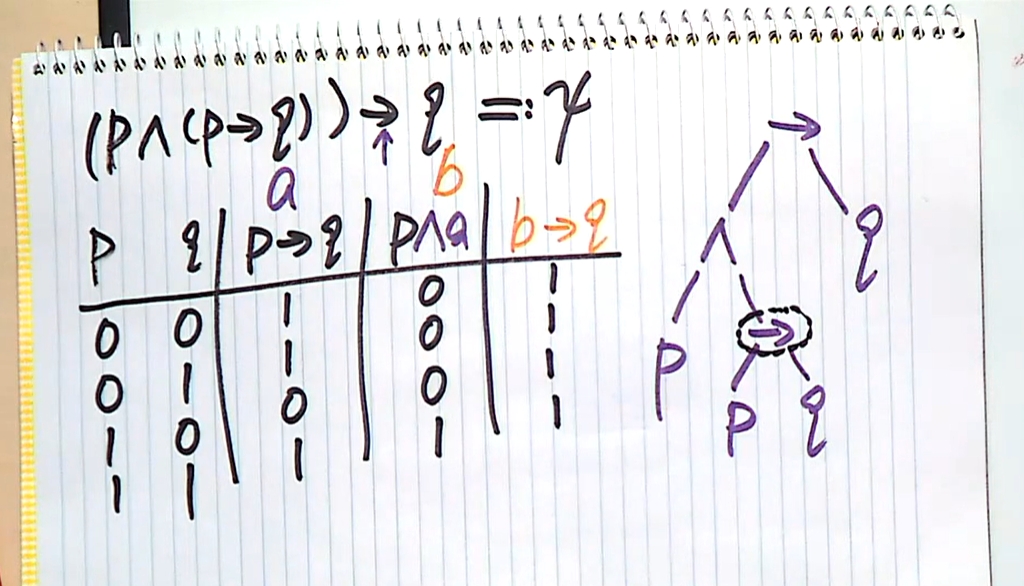
Logical equivalence

Definition

Two propositions are logically equivalent if they are true for the same truth values of their atomic propositions.

Example

A : “It is raining”

is logically equivalent to

¬(¬A) : “It is not the case that it is not raining”

A	¬A	¬(¬A)
True	False	True
False	True	False

Applications II: Program Logic

Example

if $x >0$ or $(x <=0 and y >100)$:

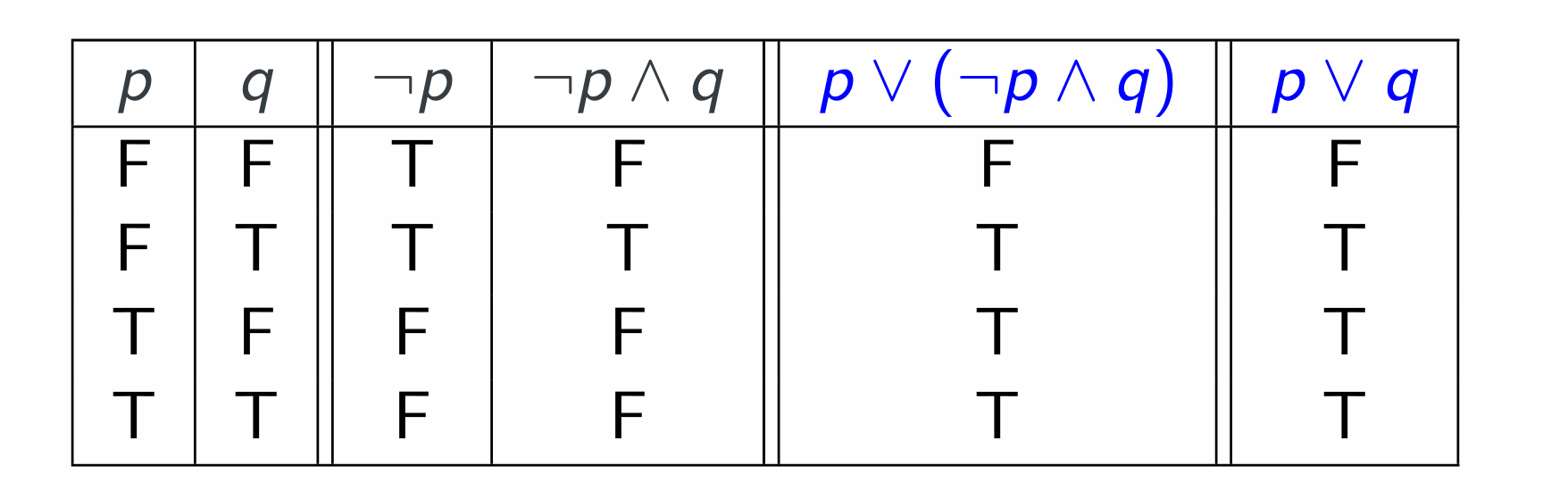
$Let \quad p \overset{def}{=} ( x >0) \quad and \quad q \overset{def}{=} (y > 100)$ $p ∨ (¬p∧q)$

$p ∨(¬p ∧q)$ is equivalent to $p ∨q$.

Hence the code can be simplified to

$if x >0 \quad or \quad y >100:$

Entailment and Validity

蕴涵和有效性

An argument consists of a set of propositions called premises and a declarative sentence called the conclusion.

Example of Toyota and Ford

Premises:

Frank took the Ford or the Toyota.
If Frank took the Ford he will be late.
Frank is not late.

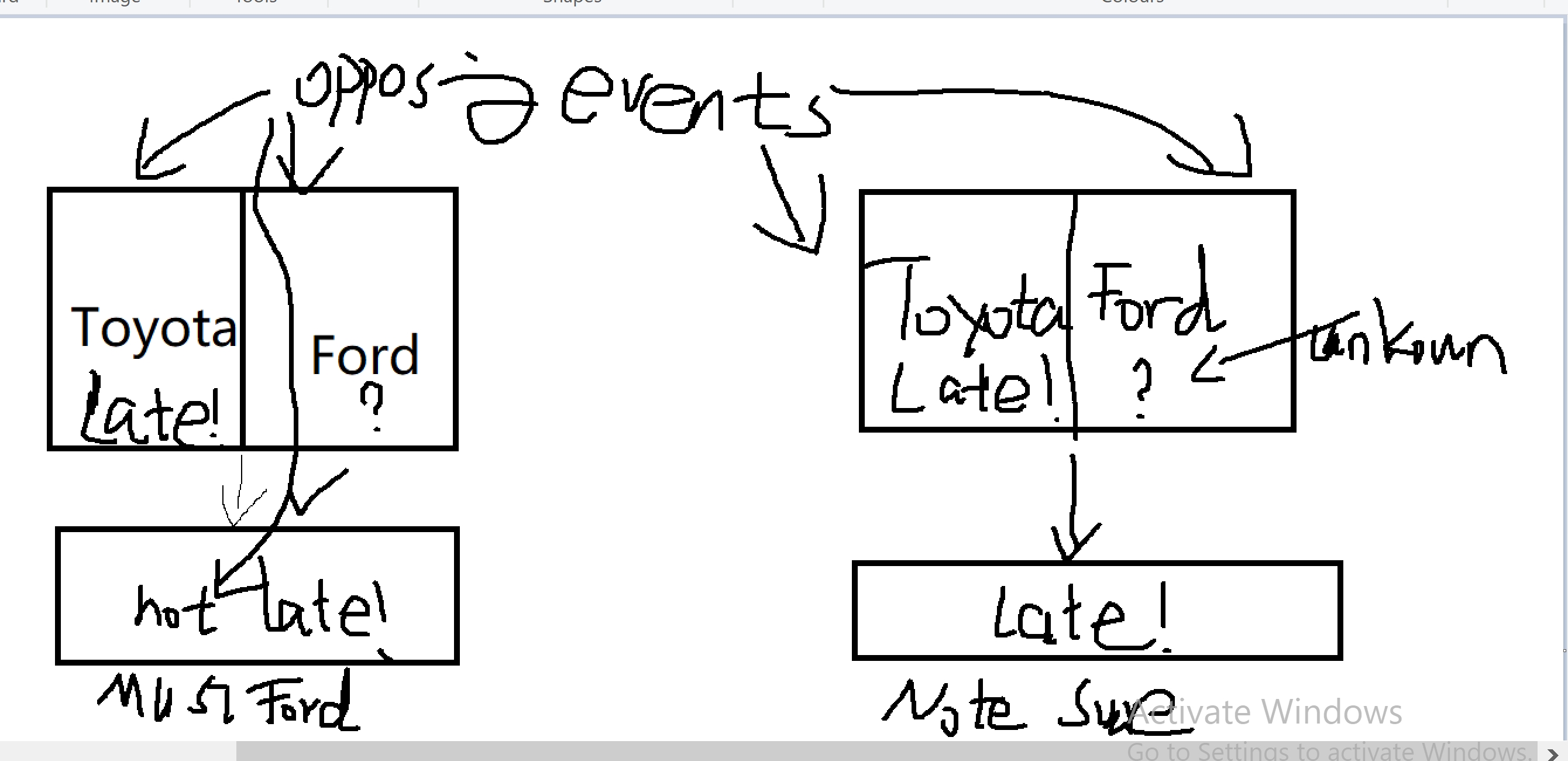
Conclusion:

Frank took the Toyota

An argument is valid if the conclusions are true whenever all the premises are true. Thus: if we believe the premises, we should also believe the conclusion.

(Note: we don’t care what happens when one of the premises is false.)

Other ways of saying the same thing:

The conclusion logically follows from the premises.
The conclusion is a logical consequence of the premises.
The premises entail the conclusion.

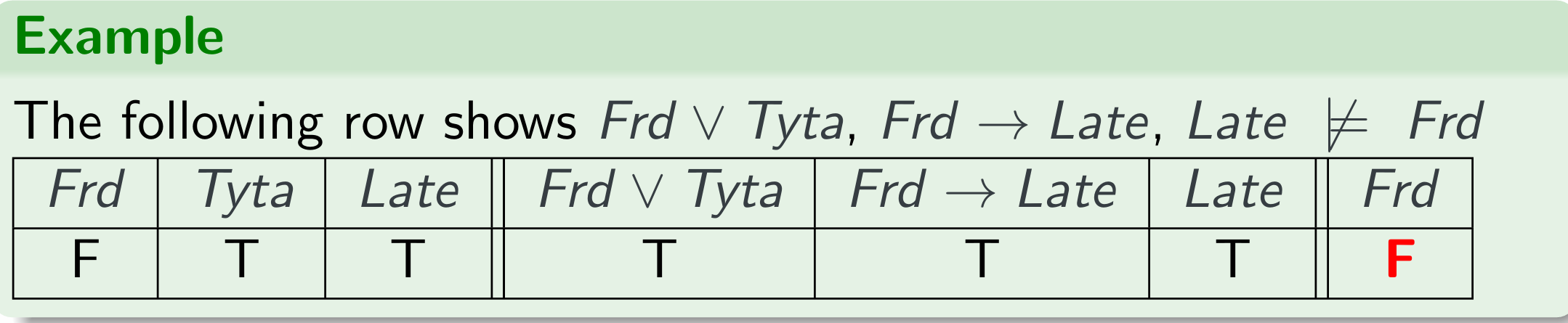
The argument above is valid. The following is invalid:

Premises

Frank took the Ford or the Toyota.
If Frank took the Ford he will be late.
Frank is late.

Conclusion

Frank took the Ford.

The argument above is invalid, please refer to the pic I draw, and the reasoning is that, we cannot judge Frank took the Ford, because he could take the Toyota and hence he was late!

Example of spaceship and the imposters

You are on a spaceship with crewmates – who always tell the truth; and imposters– who always lie.

Premises:

Red says: “Blue is an imposter”

Green says: “Red and Blue are both crewmates”

Blue says: “Red is a crewmate, or Green is an imposter”

Everyone is either a crewmate, or an imposter, but not both

-> Conclusion: Green is an imposter.

Jiaojiao: “Later we use propositional logic to prove it”

Applications III: Reasoning About Requirements/Specifications

Suppose a set of English language requirements $R$ for a software/hardware system can be formalised by a set of formulas {$φ_1$,…,$φ_n$}.

Suppose $C$ is a statement formalised by a formula $ψ$. Then

The requirements cannot be implemented if $φ_1 ∧ … ∧ φ_n$ is not satisfiable.
If $φ_1,…,φ_n$ entails $ψ$ then every correct implementation of the requirements $R$ will be such that $C$ is always true in the resulting system.
If $φ1,…,φ{n−1}$ entails $φ_n$, then the condition φn of the specification is redundant and need not be stated in the specification.

Example of alarm ringing

Requirements R: A burglar alarm system for a house is to operate as follows. The alarm should not sound unless the system has been armed or there is a fire. If the system has been armed and a door is disturbed, the alarm should ring. Irrespective of whether the system has been armed, the alarm should go off when there is a fire.

Conclusion C: If the alarm is ringing and there is no fire, then the system must have been armed.

Questions

Will every system correctly implementing requirements R satisfy C?
Is the final sentence of the requirements redundant?

Expressing the requirements as formulas of propositional logic, with

S = the alarm sounds = the alarm rings
A = the system is armed
D = a door is disturbed
F = there is a fire

we get

Requirements:

$S →(A∨F)$
$(A∧D)→S$
$F →S$

Conclusion:

$(S ∧ ¬F) → A$

Our two questions then correspond to

Does $S →(A∨F), (A∧D)→S, F →S$ entail $(S ∧¬F) →A$ ?
Does $S →(A∨F), (A∧D)→S$ entail $F →S$ ?

Propositional Logic, formally

Syntax vs Semantics

The first step in the formal definition of logic is the separation of syntax and semantics

Syntax is how things are written: what defines a formula
Semantics is what things mean: what does it mean for a formula to be “true”?

example

“Rabbit” and “Bunny” are syntactically different, but semantically the same.

Syntax: Well-formed formulas

Let $Prop =$ {p,q,r,…} be a set of propositional letters. Consider the alphabet. (Prop is proposition)

$Σ=Prop∪\{⊤,⊥,¬,∧,∨,→,↔,(,)\}.$

Prop就是之前我们说的 a(条件a语句),b（条件b语句）,c,d,e,C(常为Conclusion) 这些的，然后Σ是Prop并上逻辑推理符号。

The well-formed formulas (wffs) over Prop is the smallest set of words over $Σ$ such that:

⊤, ⊥ and all elements of Prop are wffs
If φ is a wff then ¬φ is a wf
If φ and ψ are wffs then (φ∧ψ), (φ∨ψ), (φ → ψ), and (φ ↔ψ) are wffs.

Examples

The following are well-formed formulas:

(p ∧¬⊤)
¬(p ∧¬⊤)
¬¬(p ∧¬⊤)

The following are not well-formed formulas:

p ∧∧
p ∧¬⊤
(p ∧q ∧r)
¬(¬p)

注意，∧这种操作符（二元操作符），左右必须有值，且整体被圆括号包裹。¬(¬p)不是wff是因为¬不要加括号，直接写¬¬p就是wff。

Syntax: Conventions

To aid readability some conventions and binding rules can and will be used [not in proof assistant].

Parentheses omitted if there is no ambiguity (e.g. p ∧ q)

¬ binds more tightly than ∧ and ∨, which bind more tightly than → and ↔ (e.g. $p ∧q → r$ instead of $((p ∧q) → r)$

∧ and ∨ associate to the left: $p∨q∨r$ instead of $((p∨q)∨r)$

To aid readability some conventions and binding rules can and will be used [not in proof assistant].

Parentheses omitted if there is no ambiguity (e.g. p ∧ q)
¬ binds more tightly than ∧ and ∨, which bind more tightly than → and ↔ (e.g. p ∧q → r instead of ((p ∧q) → r)
∧ and ∨ associate to the left: p∨q∨r instead of ((p∨q)∨r)

Other conventions (rarely used/assumed in this lecture):

′ or $\overline{·}$ for ¬
+ for ∨
· or juxtaposition for ∧
∧ binds more tightly than ∨
→and ↔associate to the right: p → q → r instead of (p →(q →r))

Syntax: Parse trees

The structure of well-formed formulas (and other grammar-defined syntaxes) can be shown with a parse tree.

$((P∧¬Q)∨¬(Q →P))$

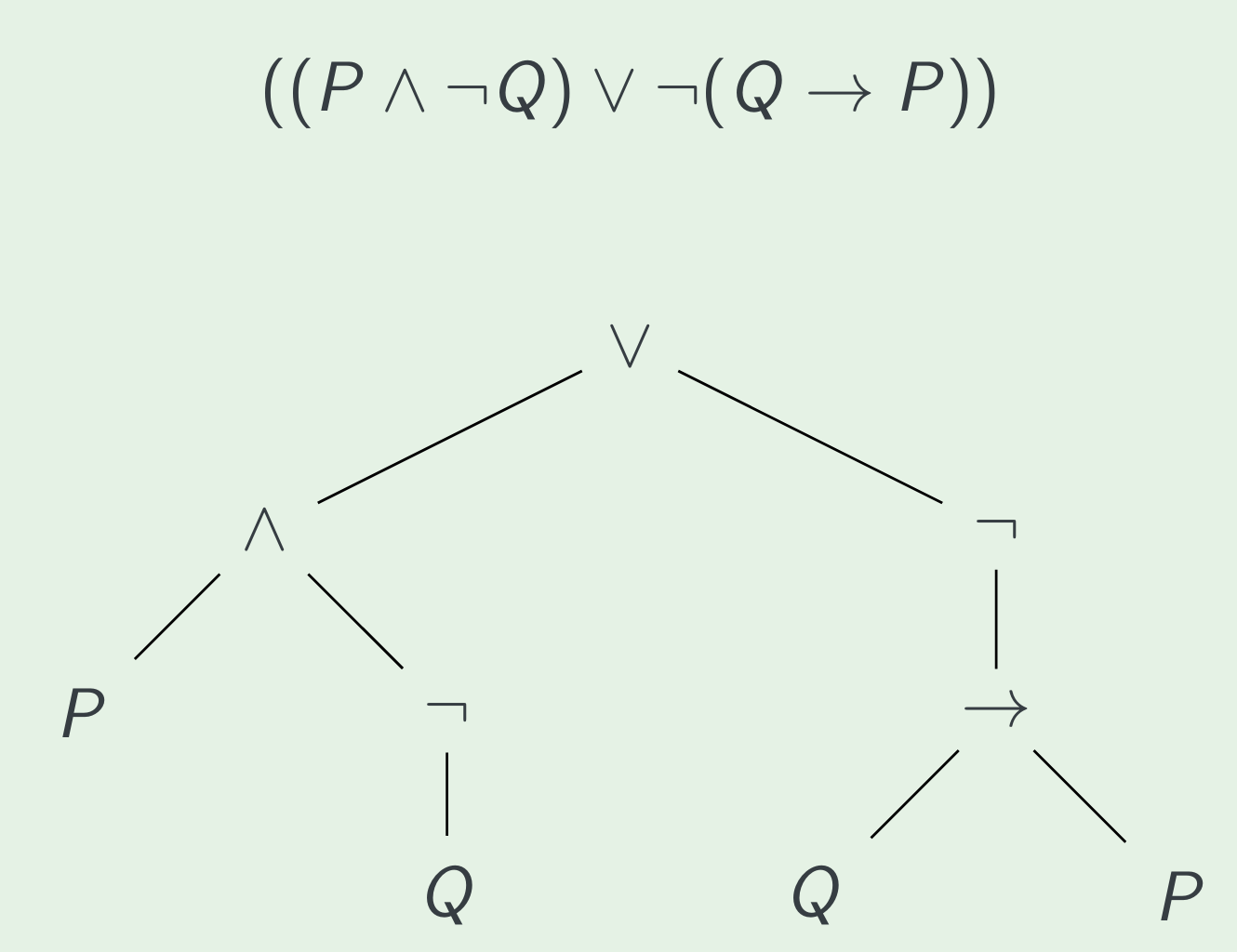
Syntax: Parse trees formally

Formally, we can define a parse tree as follows:

A parse tree is either:

(B) A node containing ⊤;
(B) A node containing ⊥;
(B) A node containing a propositional variable;
(R) A node containing ¬ with a single parse tree child;
(R) A node containing ∧ with two parse tree children;
(R) A node containing ∨ with two parse tree children;
(R) A node containing → with two parse tree children; or
(R) A node containing ↔ with two parse tree children.

Semantics: Boolean Algebras

Recall the two-element Boolean Algebra

$\mathbb{B} =\{true,false\} = \{T,F\} = \{1,0\}$

together with the operations !, &&, ∥.

Define $⇝, ↭$ as derived boolean functions:

x $⇝$y =(!x)∥y =max{1−x,y}
x $↭$y=(x $⇝$y)&&(y $⇝$x)=(1+x+y)%2)

Semantics: Truth valuations

A truth assignment is a function v : $Prop → \mathbb{B}$.

We can extend a truth valuation, v, which assigns a value to all wffs of propositional logic as follows:

v(⊤) = true,
v(⊥) = false,
v(¬φ) =!v(φ),
v(φ ∧ψ) = v(φ) && v(ψ)
v(φ ∨ψ) = v(φ) ∥ v(ψ)
v(φ →ψ)=v(φ) ⇝v(ψ)
v(φ ↔ψ)=v(φ) ↭v(ψ)

A truth assignment is a function v : $Prop → \mathbb{B}$.

We can extend a truth valuation, v, to all wffs of propositional logic as follows:

v(⊤) = 1,
v(⊥) = 0,
v(¬φ) = 1−v(φ),
v(φ ∧ψ) = min{v(φ),v(ψ)}
v(φ ∨ψ) = max{v(φ),v(ψ)}
v(φ →ψ)=max{1−v(φ),v(ψ)}
v(φ ↔ψ)=(1+v(φ)+v(ψ)) % 2

Semantics: Exercises

Exercises

Evaluate the following formulas with the truth assignment $v(p) = v(q) = false$

p →q

true

(p →q) →(p →q)

true

¬¬p

false

⊤∧¬⊥→p

false

Semantics: Truth tables

Row for every truth assignment — assignment of T/F to elements of Prop

Columns for subformulas

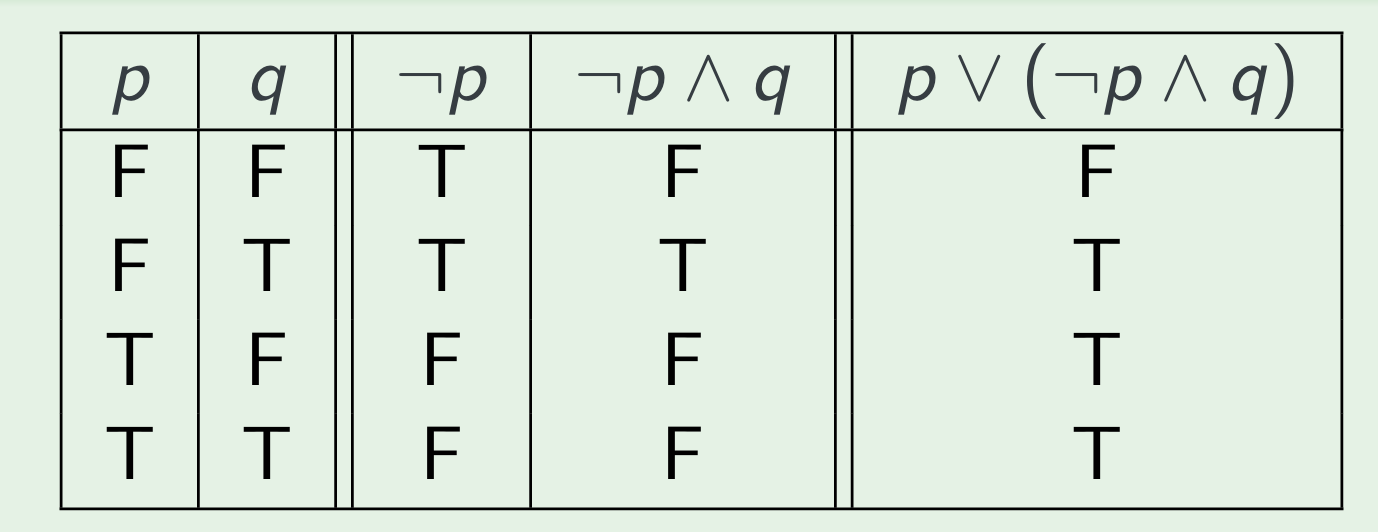
Satisfiability and Equivalence

A formula φ is

satisfiable if v(φ) = true for some truth assignment v (v satisfies φ)
a tautology if v(φ) = true for all truth assignments v
unsatisfiable or a contradiction if v(φ) = false for all truth assignments v

Example: Party invitations

Translation to logic: let J,S,K represent “John (Sarah, Kim) comes to the party”. Then the constraints are:

J → ¬S
S →K
K →J

Thus, for a successful party to be possible, we want the formula $ψ =(J →¬S)∧(S →K)∧(K →J)$ to be satisfiable. Truth values for J,S,K making this true are called satisfying
assignments, or models.

We figure out where the conjuncts are false, below. (so blank = T)

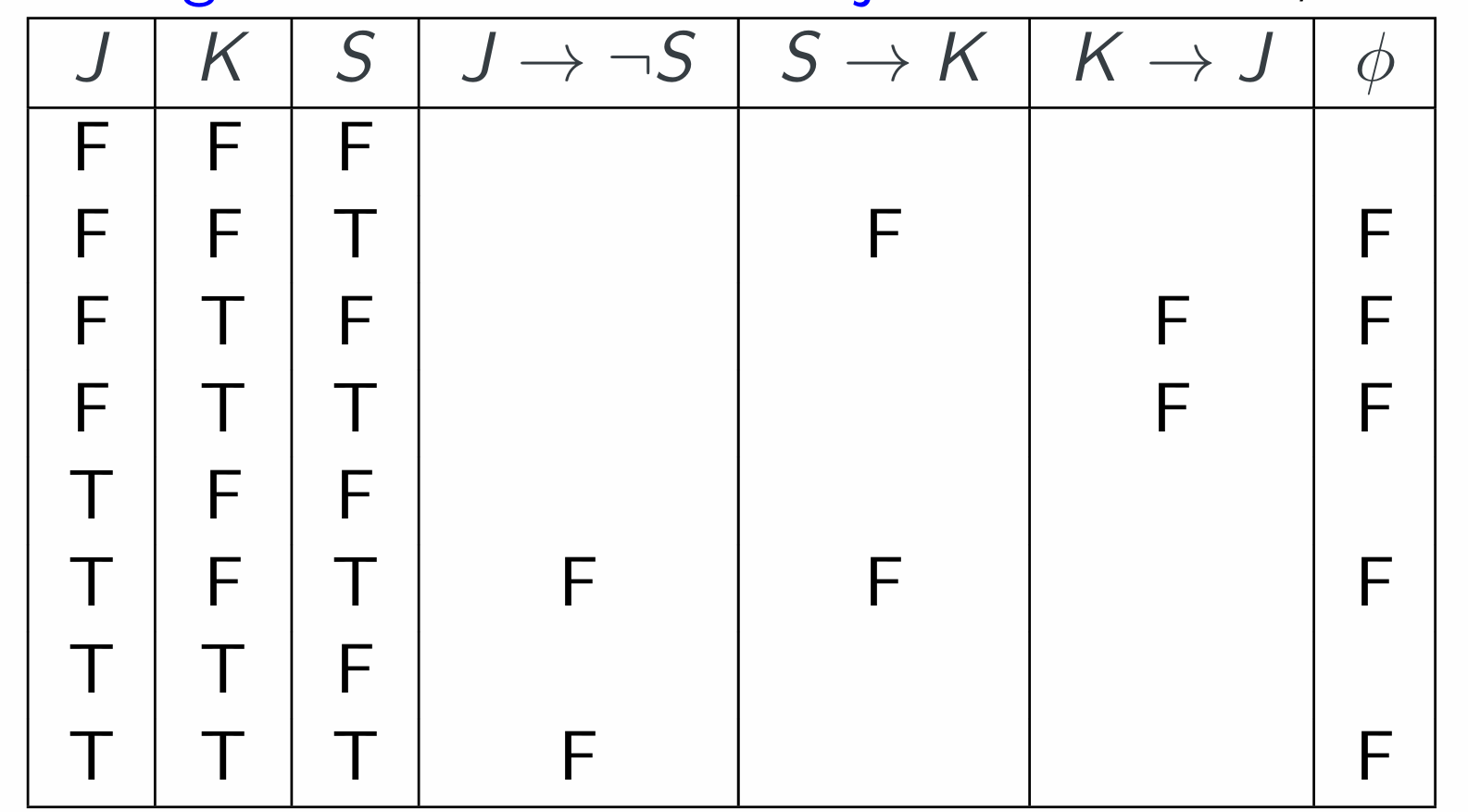
Conclusion: a party satisfying the constraints can be held. Invite nobody, or invite John only, or invite Kim and John.

Logical equivalence

Definition

Two formulas, φ and ψ, are logically equivalent, $φ ≡ ψ, if v(φ) = v(ψ)$ for all truth assignments v.

Fact

$≡$ is an equivalence relation.

properties

For all propositions P,Q,R:

Commutativity

$P ∨Q ≡ Q∨P \\ P ∧Q ≡ Q∧P$

Associativity

$(P ∨Q)∨R ≡ P∨(Q∨R) \\ (P ∧Q)∧R ≡ P∧(Q∧R)$

Distributivity

$P ∨(Q ∧R) ≡ (P∨Q)∧(P∨R)\\ P ∧(Q ∨R) ≡ (P∧Q)∨(P∧R)$

Identity

$P ∨⊥ ≡ P\\ P ∧⊤ ≡ P$

Complement

$P ∨¬P ≡ ⊤\\ P ∧¬P ≡ ⊥$

Other properties:

Implication: $p → q ≡ ¬p ∨q$

Double negation: $¬¬p ≡ p$

Contrapositive: $(p → q) ≡ (¬q → ¬p)$

De Morgan’s: $¬(p ∨q) ≡ ¬p ∧¬q$

Fact

$φ ≡ψ$ if, and only if, $(φ ↔ ψ)$ is a tautology.

Strategies for showing logical equivalence:

Compare all rows of truth table.
Show $(φ ↔ψ)$ is a tautology.
Use transitivity of $≡$.

exercise

Prove or disprove:

(a) $p → (q →r) ≡ (p →q)→(p →r)$

Theories and entailment

A set of formulas is a theory:

$T = \{φ1,φ2,...,φn\}$

A truth assignment v satisfies a theory T, $if \quad v(φi) = true \text{ for all } φi ∈ T$

A theory T entails a formula $ψ$, $T |= ψ$, if $v(ψ) = true$ for all truth assignments v which satisfy T

Take Notice

Other notation (when T = {$φ_1$,$φ_2$,…,$φ_n$})

$φ_1,φ_2,...,φ_n |= φ\\ φ_1,φ_2,...,φ_n, ∴ φ\\ φ_1,φ_2,...,φ_n =⇒ φ$

Entailment and Implication

Theorem

The following are equivalent:

$φ_1,φ_2,...,φ_n |= ψ\\ ∅ |= ((φ_1 ∧φ_2)∧...φ_n) → ψ\\ ((φ_1 ∧ φ_2) ∧...φ_n) → ψ is a tautology\\ ∅ |= φ_1 →(φ_2 →(... →(φ_n →ψ)...))\\ φ_1 |= φ_2 →(... → (φ_n → ψ)...)$

These last two equivalences can be proven using the following fact.

Fact

Let T be a theory, and A and B be propositions. Then

$T |= A→B \text{ is equivalent to } T ∪\{A\} |= B.$

Showing entailment

Strategies for showing $φ_1,φ_2,…,φ_n |= ψ$:

Draw a truth table with columns for $φ_1,…,φ_n$ and $ψ$. Check $ψ$ is true in rows where all the $φ_i$ are true.
Show $((φ_1 ∧φ_2)∧…φ_n) → ψ$ is a tautology.
Show $φ_1 →(φ_2 →(… → (φ_n →ψ)…))$ is a tautology.
Show $φ_1 |= φ_2 → (… → (φ_n → ψ)…)$
Syntactic techniques: Natural deduction, Resolution, etc (not covered here)

Entailment example

Premises:

Frank took the Ford or the Toyota.
If Frank took the Ford he will be late.
Frank is not late.

Conclusion:

Frank took the Toyota

注意如果三个premise全T，只有这个红色的T这一行；则从结论可以看出蕴含这伙只可能开Tyta。而无法蕴含开Ford是真。(这句话是~错的昂~！原子命题是T或F根本不是判断依据，根本无所谓)

我们找的是真值表中，所有约束条件为T的情况（与原子命题是T、F无关！）我们只找约束全T的情况下，Conclusion是否为T，则说明几个约束(constraint)推理到结论（Conclusion）是蕴含（entailment）有效的（valid）。

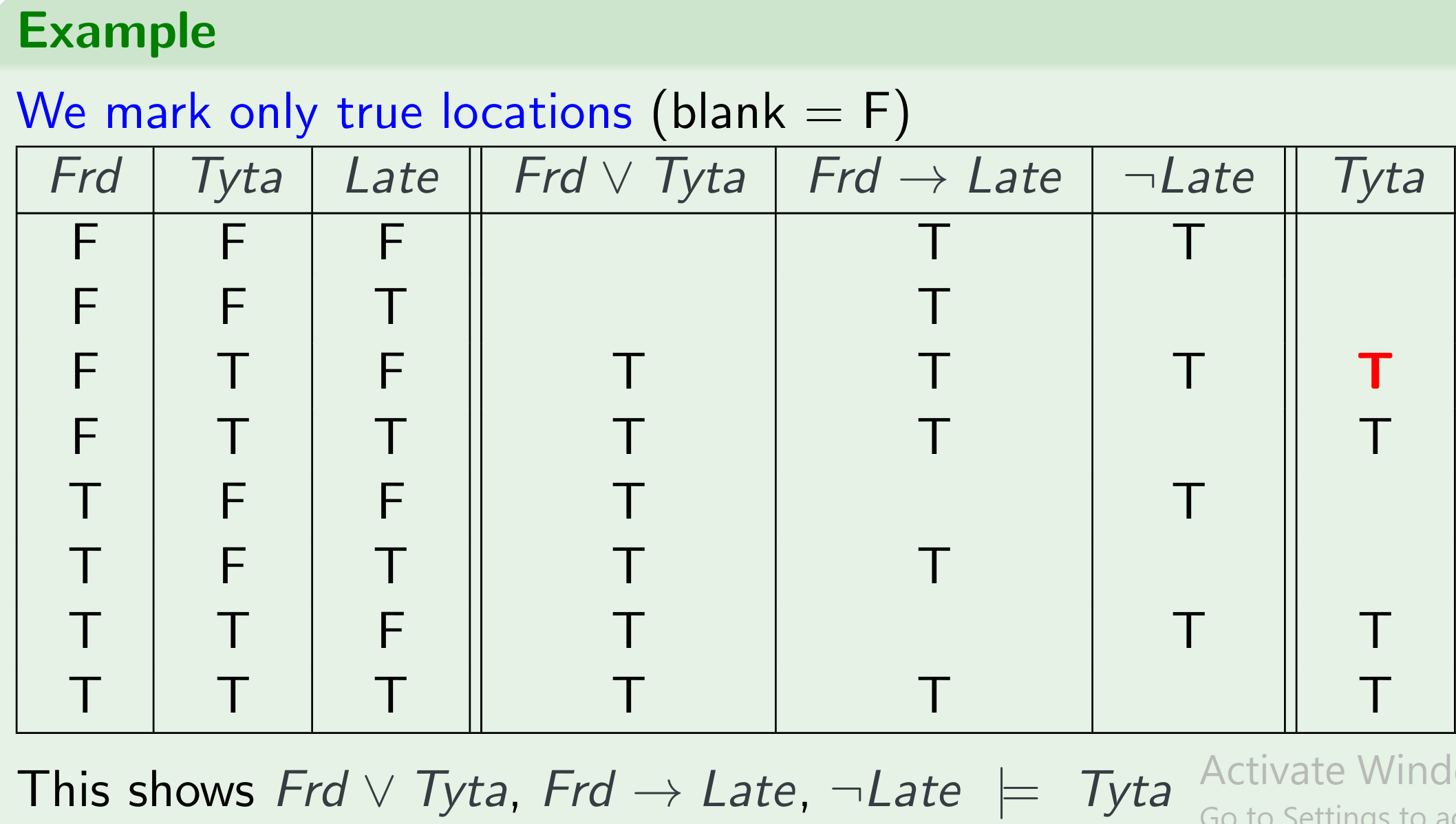
再看下Sample的题：

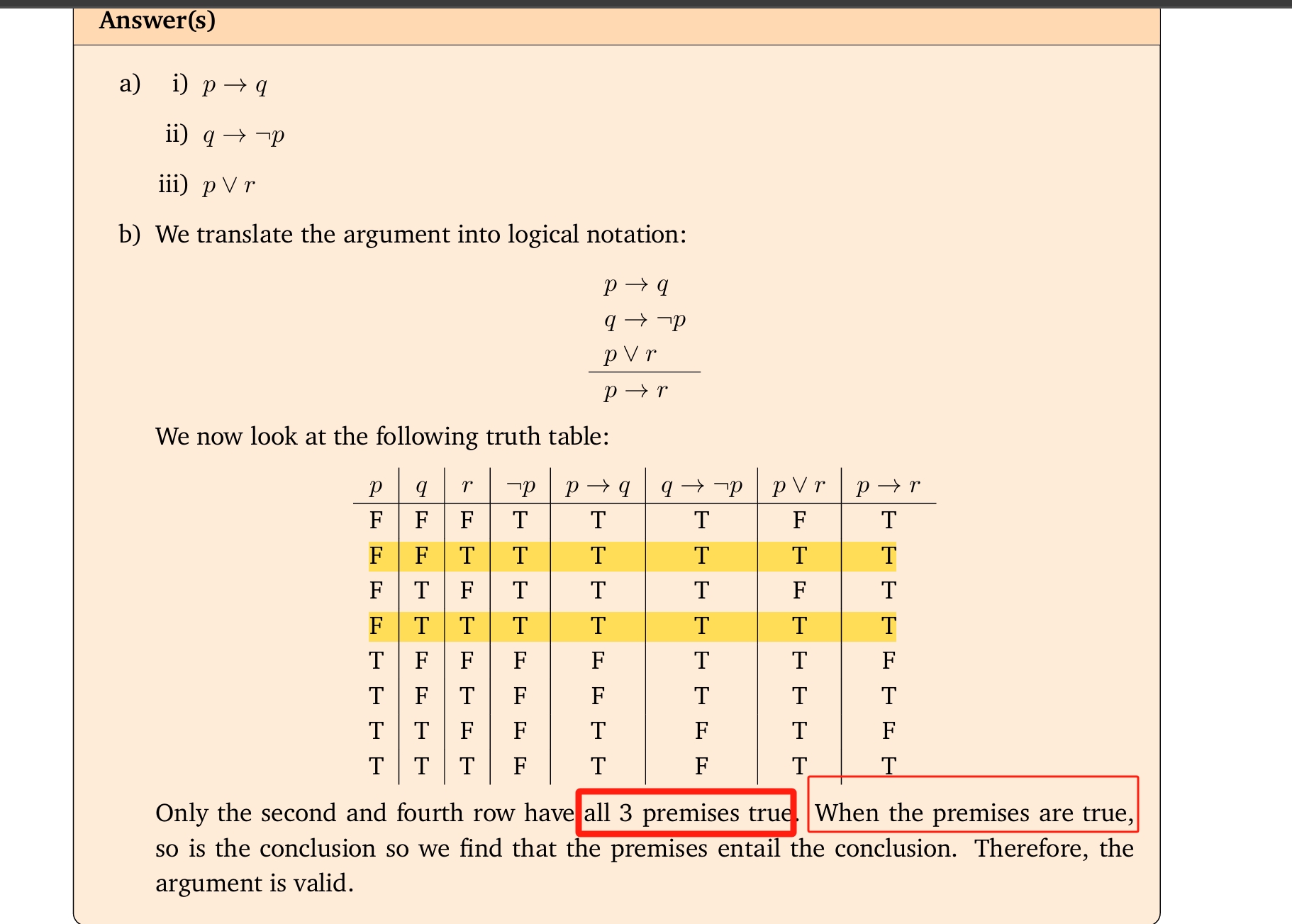
看到几个premise全是T的行，因此 the premises entail the conclusion. 因此 the argument is valid.

Example:Crewmates and Imposters

Because I did the note for the first time, there may be some mistake and insufficient understanding of the knowledge. Please refer to my the other articles to help: 1. improper-atomic-and-entailment 2. truth-table-solves-imposter-and-crewmate

Premises:

Everyoneiseitheracrewmate,oranimposter,
butnotboth
Red: “Blue is an imposter”
Green: “Red and Blue are both crewmates”
Blue: “Red is a crewmate,or Green is an imposter”

Conclusion:

Green is an imposter

Translation to logic: Let R, G, B represent “Red (Green, Blue) is a crewmate”.

Then the constraints are:

Premises:

Everyone is either a crewmate, or an imposter, but not both
$φ_1 =R ↔¬B$
Green: “Red and Blue are both crewmates”
Blue: “Red is a crewmate, or Green is an imposter”

Conclusion:

Green is an imposter

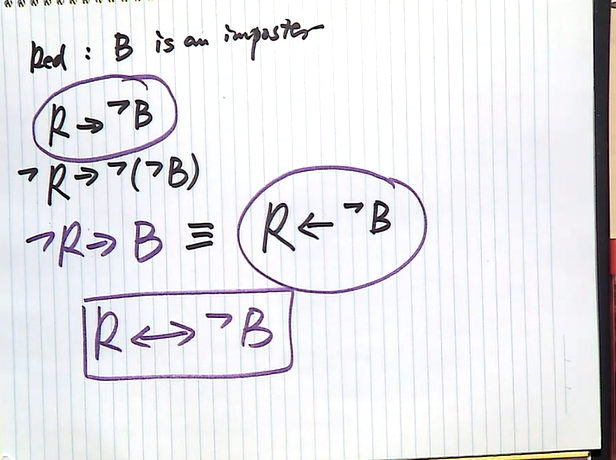
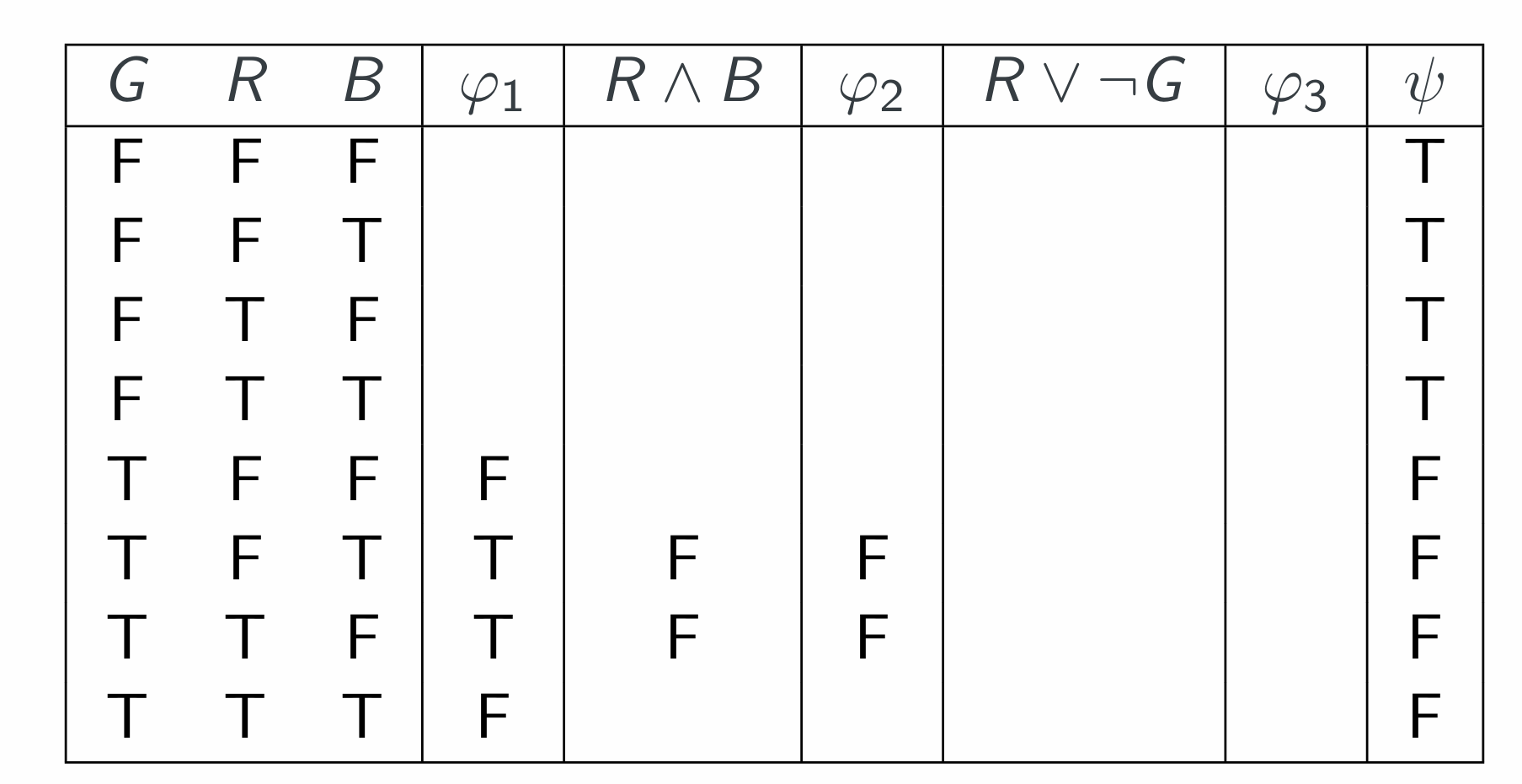
CNF and DNF Revisited

Definition

A literal is an expression p or ¬p, where p is a propositional atom.
A propositional formula is in CNF (conjunctive normal form) if it has the form

$\underset{i}{\land}C_i \\ % \lor$

where each clause Ci is a disjunction of literals e.g. $p ∨q∨¬r$.

A propositional formula is in DNF (disjunctive normal form) if it has the form

$\underset{i}{\lor}C_i \\$

where each clause $C_i$ is a conjunction of literals e.g. $p ∧q∧¬r$.

Take Notice

CNF and DNF are syntactic forms.

Theorem

For every Boolean expression $φ$, there exists an equivalent expression in conjunctive normal form and an equivalent expression in disjunctive normal form.

Beyond Propositional Logic

Limitations to Propositional Logic

Propositional logic is unable to capture several useful phenomena:

Spatial/temporal dependence (e.g. P holds after Q holds)
Belief and knowledge (e.g. I know that you know that X holds)
Relationships between propositions (e.g. “The sky is blue” and “my eyes are blue”)
Quantification (e.g. “All men are mortal”)

Beyond Propositional Logic

Modal logic: Introduce modalities to capture statement qualifying.

Example

Temporal logic:

$F φ: φ$ will be true at some point in the future
$G φ: φ$ will be true at all points in the future
$φU ψ: φ$ will be true until $ψ$ holds

First order logic/Predicate logic: Add relations (predicates) and quantifiers to capture relationships between propositions.

Example

P: All men are mortal: $∀x Man(x) → Mortal(x)$
Q: Socrates is a man: $Man(Socrates)$
R: Socrates is mortal: $Mortal(Socrates)$

In propositional logic, there is no connection between P, Q and R: it is not the case that $P,Q |= R$.

In first-order logic you can show $P,Q |= R$.

Second order logic: Add quantification of relations.

Limitations

More expressive logics require more complex semantics.

Logical equivalence harder to show
Entailment harder to show
Connections between different concepts not so straightforward

Example

In Temporal Logic, a valuation is a function $v : Prop × \mathbb{N} → \mathbb{B}$ - i.e. truth tables that change over time.

Welcome to point out the mistakes and faults!