PREFACE

Lecture 11: Recursion

• Introduction: Recursion in Computer Science
• Recursion
  • Example: Factorial
  • Example: Euclid’s gcd algorithm
  • Example: Towers of Hanoi
    • move 1 disks
    • move 2 disks
    • move 3 disks
    • move 4 disks
• Recursive Data Structures
  • Example: Natural numbers
  • Example: Odd/Even numbers
  • Example: Fibonacci numbers
  • Example: Linked lists
  • Example: Words over $Σ$
  • Example: Expressions in the Proof Assistant
  • Example: Propositional formulas
  • Exercises
• Recursive Programming
  • Programming over recursive datatypes
  • Exercise
  • Pitfall: Correctness of Recursive Definition
    • Example (Incorrect definition)
    • Example (Incorrect definition)
  • Mutual Recursion
    • Example (Fibonacci, again)
• Solving Recurrences
  • Example 1 (Unwinding)
  • Example 2 (unwinding)
  • Example 3 (Approximating with big-O)
  • Master Theorem
    • Example 1
    • Example 2
    • Example 3 wind
  • The Master Theorem: Pitfalls
  • The Master Theorem: Linear differences
    • exercise

Introduction: Recursion in Computer Science

Fundamental concept in Computer Science

• Defining complex objects from simpler ones
• Unbounded complexity with a finite description

Recursive Data Structures:

Finite definitions of arbitrarily large objects

• Natural numbers
• Words
• Linked lists
• Formulas
• Binary trees

Recursive Algorithms:

Solving problems/calculations by reducing to smaller cases

• Factorial
• Euclidean gcd algorithm
• Towers of Hanoi
• Mergesort, Quicksort

Analysis of Recursion:

Reasoning about recursive objects

• Induction, Structural Induction
• Recursive sequences (e.g. Fibonacci sequence)
• Asymptotic analysis of recursive functions

Recursion

Consists of a basis (B) and recursive process (R).

A sequence/object/algorithm is recursively defined when (typically)

(B) some initial terms are specified, perhaps only the first one;

(R) later terms stated as functional expressions of the earlier
terms.

Take Notice

(R) also called recurrence formula (especially when dealing with sequences)

Example: Factorial

$Factorial$:

(B) $0! =1$

(R) $(n+1)! = (n+1)·n!$

$fact(n)$:

(B) $if(n = 0): 1$

(R) $else: n ∗ fact(n −1)$

TAKE NOTICE: $0! =1$

Example: Euclid’s gcd algorithm

$$gcd(m,n) \begin{cases} m & \text{if m = n} \\ gcd(m −n,n) & \text{if m >n} \\ gcd(m,n−m) & \text{if m <n} \end{cases}$$

Example: Towers of Hanoi

• There are 3 towers (pegs)
• n disks of decreasing size placed on the first tower
• You need to move all disks from the first tower to the last tower
• Larger disks cannot be placed on top of smaller disks
• The third tower can be used to temporarily hold disks

Questions:

• Describe a general solution for n disks
• How many moves does it take?

move 1 disks

One step obviously.

move 2 disks

Three steps obviously.

move 3 disks

We move 3 towers that takes 7 steps. —-(1)

move 4 disks

And if we need to move 4 towers, we move the top 3 towers into the middle pillar ((1) move to the second pillar rather not third one, but takes the same steps), 7 steps

then take 1 step to move the biggest disk to the third pillar —- (2)

then take 7 steps to the third pillar —- (3)

hence 4 disks take $7+1+7=15$ steps.

disks	steps
1	1
2	3
3	7
4	15

Hence the recursion formula is

$$M(n) ≤ 2M(n−1)+1$$

Recursive Data Structures

Example: Natural numbers

A natural number is either 0 (B) or one more than a natural number (R).

Formal definition of N:

• (B) $0 ∈ \mathbb{N}$
• (R) If $n ∈ \mathbb{N} \quad then (n+1) ∈ \mathbb{N}$

Example: Odd/Even numbers

The set of even numbers can be defined as:

• (B) 0 is an even number
• (R) If $n$ is an even number then $n+2$ is an even number

The set of odd numbers can be defined as:

• (B) 1 is an odd number
• (R) If $n$ is an odd number then $n+2$ is an odd number

Example: Fibonacci numbers

The Fibonacci sequence starts 0, 1, 1, 2, 3, … where, after 0, 1, each term is the sum of the previous two terms.

Formally, the sequence of Fibonacci numbers: $F_0, F_1, F_2, \dots$ where the n-th Fibonacci number $F_n$ is defined as:

$$(B) F_0 = 0, \\ (B) F_1 = 1, \\ (R) F_n = F_{n−1} +F_{n−2}$$

Take Notice

Could also define the Fibonacci sequence as a function

$FIB : \mathbb{N} \to \mathbb{F}.$

the $\mathbb{F}$ represents the set of Fibonacci numbers.

$$F=\{ F_0, F_1, F_2, F_3, \dots \} = \{ 0, 1, 1, 2, 3, 5, 8, 13, \dots \}$$

Example: Linked lists

A linked list is zero or more linked list nodes:

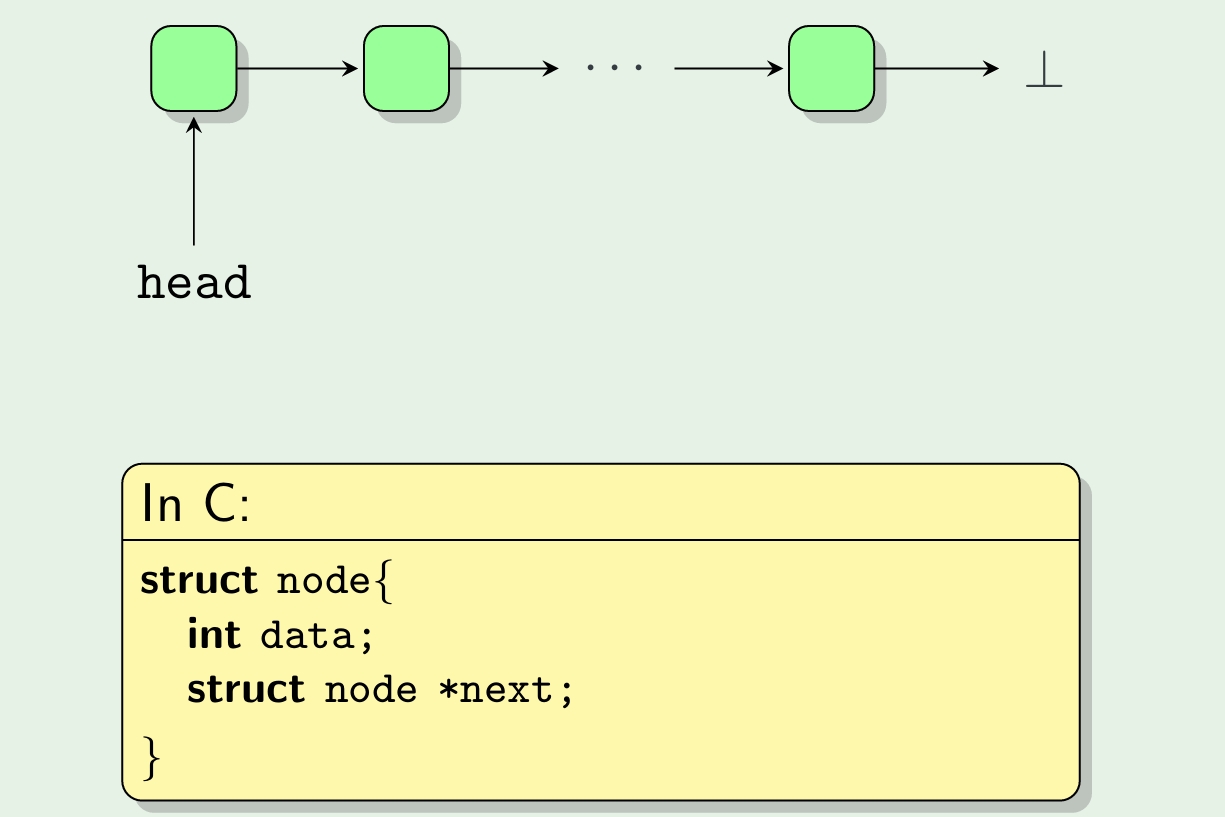
We can view the linked list structure abstractly. A linked list is either:

• (B) an empty list, or
• (R) an ordered pair (Data,List).

Example: Words over $Σ$

A word over an alphabet $Σ$ is either $λ(B)$ or a symbol from $Σ$ followed by a word (R).

Formal definition of $Σ^∗$:

• $(B) λ ∈ Σ^∗$
• $(R) \text{If } w ∈ Σ^∗ \text{then } aw ∈ Σ^∗ \text{ for all } a ∈ Σ$

Take Notice

This matches the recursive definition of a Linked List data type.

Example: Expressions in the Proof Assistant

(B) $A,B,…,Z,a,b,…z$ are expressions \
(B) $∅$ and $U$ are expressions \
(R) If $E$ is an expression then so is $(E)$ and $E^c$ \
(R) If $E_1$ and $E_2$ are expressions then:

$$(E_1 ∪ E_2), \\ (E_1 ∩ E_2), \\ (E_1 \backslash E_2), and \\ (E_1 ⊕ E_2) \text{ are expressions}.$$

Example: Propositional formulas

A well-formed formula (wff) over a set of propositional variables, $Prop$ is defined as:

(B) $⊤$ is a wff

(B) $⊥$ is a wff

(B) $p$ is a wff for all $p ∈ Prop$

(R) If $φ$ is a wff then $¬φ$ is a wff

(R) If $φ$ and $ψ$ are wffs then:

• $(φ ∧ψ)$,
• $(φ ∨ψ)$,
• $(φ →ψ)$, and
• $(φ ↔ψ)$ are wffs.

Exercises

(a) Give a recursive definition for the sequence

$$(2, 4, 16, 256, ...)$$

To generate $an = 2^{2^n}$ use $a_n = (a{n−1})^2$.

(The related “Fermat numbers” $F_n = 2^{2^n} + 1$ are used in cryptography.)

(b) Give a recursive definition for the sequence

$$(2, 4, 16, 65536, ...)$$

To generate a “stack” of n 2’s use $bn = 2^{b{n−1}}$.

Recursive Programming

Programming over recursive datatypes

Recursive datatypes make recursive programming/functions easy.

The factorial function:

$$fact(n): \\ (B) \quad if(n = 0): 1 \\ (R) \quad else: n ∗ fact(n −1)$$

Summing the first n natural numbers:

$$sum(n): \\ (B) \quad if(n = 0): 0 \\ (R) \quad else: n +sum(n −1)$$

Summing elements of a linked list:

$$sum(L): \\ (B) if(L.isEmpty()): return 0 \\ (R) else: return L.data+sum(L.next)$$

Sorting elements of a linked list (insertion sort):

$$sort(L): (B) if(L.isEmpty()): \\ return L \\ else: \\ (R) L2 =sort(L.next) \\ insert L.data into L2 \\ return L2$$

Concatenation of words (defining wv):

For all $w,v ∈ Σ^∗$ and $a ∈ Σ$ :

(B) $λv =v$

(R) $(aw)v = a(wv)$

Length of words:

(B) length(λ) = 0

(R) length(aw) = 1 + length(w)

Exercise

Let $Σ$ be a finite set.
Define append : $Σ^∗ \times Σ \to Σ^∗$ by

$$append(w, a) = wa$$

Give a (direct) definition of append [i.e. only concatenates symbols on the left].

For all $w ∈ Σ^∗$ and $a,x ∈ Σ$:

(B) append(λ, x) = x

(R) append(aw, x) = a append(w, x)

Pitfall: Correctness of Recursive Definition

A recurrence formula is correct if the computation of any later term can be reduced to the initial values given in (B).

Example (Incorrect definition)

Function g(n) is defined recursively by

$$g(n) = g(g(n −1)−1)+1, \quad g(0) = 2.$$

The definition of $g(n)$ is incomplete — the recursion may not terminate:

Attempt to compute $g(1)$ gives

$$g(1) = g(g(0)−1)+1 = g(1)+1 = ... = g(1)+1+1+1...$$

When implemented, it leads to an overflow; most static analyses cannot detect this kind of ill-defined recursion.

However, the definition could be repaired. For example, we can add the specification specify $g(1) = 2$.

Then

$$g(2) = g(2−1)+1 = 3, \\ g(3) = g(g(2) −1)+1 = g(3−1)+1 = 4, \\ \dots$$

Example (Incorrect definition)

Check your base cases!

Function f (n) is defined by

$$f(n) = f(⌈n/2⌉), f(0) = 1$$

When evaluated for n = 1 it leads to

$$f (1) = f(1) = f(1) = ...$$

This one can also be repaired. For example, one could specify that
$f(1) = 1$.

This would lead to a constant function $f(n) = 1$ for all $n ≥ 0$.

Mutual Recursion

Sometimes recursive definitions use more than one function, with each calling each other.

Example (Fibonacci, again)

Recall:

$$(B) f(0) = 0; \quad f(1) = 1, \\ (R) f(n) = f(n −1)+f(n−2)$$

Alternative, mutually recursive definition:

$$(B) f (1) = 1; g(1) = 0 \\ (R) f (n) = f(n −1)+g(n−1) \\ (R) g(n) = f(n −1)$$ $$\left( \begin{matrix} f(n)\\ g(n) \end{matrix} \right) = \left( \begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix} \right) \left( \begin{matrix} f(n −1) \\ g(n −1) \end{matrix} \right)$$

Solving Recurrences

Question: How can we (asymptotically) compare recursively defined functions?

Some practical approaches:

• Unwinding the recurrence
• Approximating with big-O
• The Master Theorem

Take Notice

Each approach gives an informal “solution”: ideally one should prove a solution is correct (using e.g. induction).

Example 1 (Unwinding)

$$f(0) = 1 \\ f(n) = 2f(n −1)$$

Unwinding:

$$f(n) = 2f(n−1) \\ = 2(2f(n−2)) = 4f(n−2) \\ = 4(2f(n−3)) = 8f(n−3) \\ \vdots \quad \vdots\\ = 2^if(n−i) \\ \vdots \quad \vdots\\ = 2^nf(0) = 2^n$$

Example 2 (unwinding)

$$f(1) = 0 \quad f(n) = 1 + f(\lfloor \frac{n}{2} \rfloor)$$

Unwinding:

$$f(n) = 1+f(n/2) \\ = 1+(1+f(n/4)) =2+f(n/4) \\ = 2+(1+f(n/8)) \\ \vdots \quad \vdots\\ = i+f(n/2^i) \\ \vdots \quad \vdots\\ = log(n)+f(0) = log(n)$$

Take notice! The answer above may be wrong, because my proof is here:

Example 3 (Approximating with big-O)

$$f(1) = 1 \quad f(2) = 1 \quad f(n) =f(n−1)+f(n−2)$$

Note, the section is approximate big-O. If you want to unwind the fabonacci sequence, refer to unwind-recursion-formula.

Assuming $f(n)$ is increasing (The step is only to compare f(n)’s growth, to get its formula until a constant):

$$f(n −2) ≤ f(n−1)$$

so

$$f(n) ≤ 2f(n −1)$$

so (by unwinding):

$$f(n) ≤ 2^n$$

so:

$$f(n) ∈ O(2^n)$$

Master Theorem

The following result covers many recurrences that arise in practice (e.g. divide-and-conquer algorithms)

Let $a ≥ 1$ be an integer, $b > 1$ a real number, and $T(n)$ be the following recurrence

$$T(n) = a \cdot T(\frac{n}{b}) + f(n)$$

where $f(n) ∈ Θ(n^c(log \text{ }n)^k)$.

By denoting $d = log_b(a)$, then we have:

• Case 1: If $c < d$ then $T(n) = Θ(n^d)$
• Case 2: If $c = d$ then $T(n) = Θ(n^c(logn)^{k+1})$
• Case 3: If $c > d$ then $T(n) = Θ(f(n))$

It’s a little complicated to understand, please refer to wiki: Master theorem).

Example 1

$$T(n) = T(\frac{n}{2} ) + n^2, \quad T(1)=1$$

Here a = 1, b = 2, c = 2, k = 0 and d = 0. So we have Case 3 and the solution is

$$T(n) = Θ(n^c) = Θ(n^2)$$

Example 2

Mergesort has

$$T(n) = 2T(\frac{n}{2} ) + (n-1)$$

for the number of comparisons.

Here a = b = 2, c = 1, k = 0 and d = 1. So we have Case 2, and the solution is

$$T(n) = Θ(n^c log(n)) = Θ(nlog(n))$$

Example 3 wind

Unwinding example:

$$T(1) = 0 \\ T(n) = 1+T(⌊ \frac{n}{2} ⌋)$$

Here a = 1, b = 2, c = 0, k = 0, and d = 0. So we have Case 2, and the solution is

$$T(n) = Θ(log(n))$$

The Master Theorem: Pitfalls

Take Notice

• a, b, c, k have to be constants (not dependent on n).
• Only one recursive term.
• Recursive term is of the form $T(n/b)$, not $T(n − b)$.
• Solution is only an asymptotic bound.

Examples

The Master theorem does not apply to any of these:

$$T(n) =2^nT(n/2)+n^2 \\ T(n) =T(n/5)+T(7n/10)+n \\ T(n) =2T(n−1)$$

First equation, the a $(2^n)$ is related to n; Second there are two T terms; Third the item is n-1 rather not n/?.

The Master Theorem: Linear differences

Take Notice

The Master Theorem applies to recurrences where T(n) is defined in terms of T(n/b); not in terms of T(n −1).

However, the following is a consequence of the Master Theorem:

Theorem

Suppose

$$T(n) = a·T(n−1) + bn^k$$

Then

$$T(n) \begin{cases} O(n^{k+1}) \quad if a=1 \\ O(a^n) \quad if a>1 \end{cases}$$

exercise

Solve $T(n) = 3^nT(\frac{n}{2})$ with $T(1) = 1$

Let $n ≥ 2$ be a power of 2 then

$$T(n) = 3^n ·3^{\frac{n}{2}}·3^{\frac{n}{4}}·3^{\frac{n}{8}} \cdot \dots = 3^{1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\dots} = O(3^{2n})$$

---

Welcome to point out the mistakes and faults!