PREFACE

Lecture 13: Combinatorics

• Combinatorics in Computer Science
• Counting Principles
  • Basic Counting Rules: Principles
• Basic Counting Rules: Union
  • Example
  • Consequences of the Union Rule
    • Fact
    • Fact
    • Proof
    • Exercises
• Basic Counting Rules: Product
  • The Product Rule
    • Example
  • Product rule: Sequences of selections
    • Example
  • Exercises 1
  • Exercises 2
• Combinatorial Symmetry
  • Definition
  • Take Notice
  • Product rule: Symmetries and duplications
  • Example
  • Product rule: Symmetries and duplications
    • Example
• Combinations and Permutations
  • Permutations with duplicates
    • Example 1
    • Example 2
  • r-selections (or: r-combinations)
  • Simple Counting Problems
  • Exercises: choose to from committees
  • Exercises:Counting Poker Hands
  • Summary
  • “Balls in boxes”
• Alternative Techniques
  • Example
• Difficult Counting Problems (not assessed)
  • Using Programs to Count
  • Approximate Counting

Combinatorics in Computer Science

Informally, combinatorics is the mathematics of counting.

More formally, combinatorics is about understanding finite systems of discrete objects.

For example:

• How many different ways are there of getting a flush in poker?

In computer science, we use combinatorics when:

• Computing cost functions in algorithmic analysis
• Identifying (in-)efficiencies in data management
• Developing effective techniques for enumerating objects
• Probability calculations

Counting Principles

General idea: find methods, algorithms or precise formulae to count the number of elements in various sets or collections derived, in a structured way, from some basic sets.

Examples

Single base set

$$S = \{s_1,...,s_n\}$$

, and $∣S∣ = n$; find the number of

• all subsets of S
• ordered selections of r different elements of S
• unordered selections of r different elements of S
• selections of r elements from S such that …
• functions $S ⟶ S (onto, 1-1)$
• partitions of S into k equivalence classes

Starter	Main Course	Dessert
Soup	Fish	Ice-cream
Bread	Beef	Fruit
	Pork	Cheese
	Chicken

---

How many:

• 3 course meals (Starter-Main-Dessert) are possible?
• 3 course meals (Any item for each course) are possible?
• 3 course meals (Any item, no duplicates) are possible?
• Meals consisting of 3 items (order is unimportant)?

These problems are translated into these below:

How many:

• Starter-Main-Dessert?

$$2 ×4×3=24$$

• Any item for 3 courses?

$$9 ×9×9=729$$

• Any item, no duplicates, for 3 courses?

$$9 ×8×7=504$$

• Meals of 3 different items?

$$504/6 = 84$$

Note, why $504/6 = 84$? Because (order is unimportant), and the order of 3 items is $3!=6$. 504 is the number of 3 ordered items, and 84 is the number of 3 unordered items.

How to understand the number of 3 ordered items is $3!=3 \times 2 \times 1=6$? We could think it’s $3 \times 2 \times 1$ of each time we choose the left items, and it’s exactly the factorial!

---

Basic Counting Rules: Principles

Two simple rules:

• Union rule (“or”): If $S$ and $T$ are disjoint $∣S ∪T∣ =∣S∣+∣T∣$
• Product rule (“followed by”): $∣S × T∣ = ∣S∣ ⋅ ∣T∣$

These cover many examples, though the rule application is not always obvious.

Common strategies:

• Direct application of the rule
• Relate unknown quantities to known quantities (e.g. $∣S∣ +∣T∣ = ∣S ∪T∣+∣S ∩T∣$)
• Find a bijection to a set that can be counted

$$∣S∣ +∣T∣ = ∣S ∪T∣+∣S ∩T∣$$

Basic Counting Rules: Union

Union rule — S and T disjoint

$$∣S ∪T∣ =∣S∣+∣T∣$$

$S_1,S_2,…,S_n$ pairwise disjoint ($S_i ∩ S_j = ∅ \quad for \quad i ≠ j$)

$$∣S_1 ∪... ∪S_n∣ = ∑∣S_i∣$$

Example

How many numbers in $A = [1,2,…,999]$ are divisible by 31 or 41?

A:

$$\lfloor 999/31 \rfloor = 32 \text{ numbers are divisible by 31 }\\ \lfloor 999/41 \rfloor = 24 \text{ numbers are divisible by 41}\\ \text{No number in A divisible by both 31 and 41}\\ Hence, 32+24=56 \text{ divisible by 31 and 41}$$

Consequences of the Union Rule

Fact

For any sets X, Y, Z:

$$∣Y \setminus X∣ = ∣Y∣−∣X ∩Y∣ \\ ∣X ∪Y∣ = ∣X∣+∣Y∣−∣X ∩Y∣ \\ ∣X ∪Y ∪Z∣ = ∣X∣+∣Y∣+∣Z∣ −∣X ∩Y∣−∣Y ∩Z∣−∣Z ∩X∣ +∣X ∩Y ∩Z∣$$

Fact

(1) If $∣S ∪T∣ = ∣S∣+∣T∣$ then $S$ and $T$ are disjoint

(2) If $∣⋃^n{i=1} S_i∣ = ∑^n{i=1} ∣S_i∣$ then $S_i$ are pairwise disjoint

(3) If $∣T \setminus S∣ = ∣T∣−∣S∣$ then $S ⊆ T$

These properties can serve to identify cases when sets are disjoint

(resp. one is contained in the other).

Proof

We can prove these facts using the inclusion-exclusion identity for two sets. Namely, that $∣S ∩ T∣ +∣S ∪T∣ = ∣S∣+∣T∣$.

(1) Suppose ∣S∣ +∣T∣ = ∣S ∪T∣. Then inclusion-exclusion gives $∣S ∩T∣ =∣S∣+∣T∣−∣S ∪T∣ =0, so S ∩T =∅$.

(3) Suppose $∣T \setminus S∣ = ∣T∣−∣S∣$. Then inclusion-exclusion gives $∣S ∩T∣ =∣S∣$, so $S ⊆ T$.

Exercises

Q: 200 people. 150 swim or jog, 85 swim and 60 do both. How many jog?

A:

Let S ∶= {people who swim} and J ∶= {people who jog}.

Then $∣S ∪J∣ = ∣S∣+∣J∣−∣S ∩J∣$; thus $150 = 85+∣J∣−60$, hence $∣J∣ = 125$.

Note that the answer does not depend on the number of people overall (200).

---

Q: (Supp)There are 100 problems, 75 of which are ‘easy’ and 40 ‘important’. What’s the smallest possible number of problems that are both easy and important?.

A:

$$∣E ∩I∣ = ∣E∣+∣I∣−∣E∪I∣ = 75+40−∣E∪I∣ ≥ 75+40−100 = 15$$

Basic Counting Rules: Product

The Product Rule

Product rule:

$$∣S_1 ×... ×S_k∣ = ∣S_1∣⋅∣S_2∣⋯∣S_k∣ = \prod^k_{i=1}∣S_i∣$$

Take Notice

This counts the number of sequences where the first item is from $S_1$, the second is from $S_2$, and so on.

Sequences mean that it’s an ordered pair.

Special case of the product rule: If all $S_i = S$ for all i and $∣S∣ = m$ then

$$∣S_1 ×S_2 ×⋯×S_k∣ =∣S ×S ×⋯×S∣=∣S^k∣=m^k$$

Example

Let Σ = {a,b,c,d,e,f,g}.

Question. How many 5-letter words can we make?

$$∣Σ ×Σ×Σ×Σ×Σ∣=∣Σ^5∣=∣Σ∣^5 =7^5 =16,807$$

---

Question. How many words with no letter repeated?

$$7 \times 6 \times 5 \times 4 \times 3 = 2520$$

Or firstly choose 5 letters from the 7 letters, and this is a combination. Then arrange the 5 chosen letters.

$$\binom{7}{5} = \frac{7!}{5!(7-5)!} = \frac{7 \times 6}{2} = 21 \\ 5! = 120 \\ \binom{7}{5} \times 5! = 2520$$

Or permutation number:

$$P(7, 5) = 2520$$

---

$$P(n, k) = \binom{n}{k} \times k!$$ $$P(n, k)=\frac{n!}{(n-k)!}$$ $$\binom{n}{k} = \frac{n!}{k!(n-k)!}$$

Product rule: Sequences of selections

Question: How can we count sequences when the underlying set changes?

A:

To count sequences without replacement:

• Define an order on the whole underlying set

• Select from $[1,n]$, where n is the size of the “remaining” set, and a selection of i represents choosing the i-th element in that set

Example

Let Σ = {a,b,c,d,e,f,g}.

How many 5-letter words with no letter repeated?

$$\prod^4_{i=0}(∣Σ∣ −i) = 7⋅6⋅5⋅4⋅3 = 2,520$$

Exercises 1

S,T finite. How many functions $S ⟶ T$ are there?

$$∣T∣^{∣S∣}$$

For all in S has the element in T. So it’s $|T| \times |T| \times … |T| \quad \therefore ∣T∣^{∣S∣}$

Exercises 2

Q:

$S=[100…999]$, thus $∣S∣=900$.

(a) How many numbers in S contain a 3 or 7 in their digits?

(b) How many numbers in S have a 3 and a 7?

---

A:

(a) How many numbers in S contain a 3 or 7

Let $A_3$ = {at least one ‘3’} and $A_7$ = {at least one ‘7’}. Then

$$(A_3 ∪A_7)^c = \{ n ∈ [100,999]∶ \text{ n digits } ∈ \{0,1,2,4,5,6,8,9\} \}$$

Note that for each number in S, there are 7 choices for the first digit and 8 choices for the later digits. So

$$(A_3 ∪A_7)^c = |{1,2,4,5,6,8,9}| \cdot |{0,1,2,4,5,6,8,9}|^2$$

Therefore $∣A_3 ∪ A_7∣ = ∣S∣ −∣(A_3 ∪A_7)^c∣ = 900−448 = 452$.

(b) How many numbers in S have a 3 and a 7?

$$∣A_3 ∩A_7∣ = ∣A_3∣+∣A_7∣−∣A_3 ∪A_7∣ \\ = (900−8⋅9⋅9)+(900−8⋅9⋅9)−452 \\ = 2⋅252−452 = 52$$

Combinatorial Symmetry

A symmetry of a mathematical object is a bijective mapping from the object to itself which preserves “structure”.

A (combinatorial) symmetry defines an equivalence relation where the equivalence classes all have the same size.

We are often interested in counting a set “up to symmetry”. That is, counting the number of equivalence classes.

This can also be stated as a constraint that identifies a specific item in each equivalence class (symmetric constraint).

Definition

A k-to-1 function is a function that maps exactly k inputs to an output.

Take Notice

A k-to-1 function defines the equivalence relation of a combinatorial symmetry and vice-versa.

Product rule: Symmetries and duplications

Question

• How can we count sequences when we have symmetric
  constraints?
• How can we count sequences when we have duplicates?

Example

Let Σ = {a,b,c,d,e}.

• How many 5-letter words with no letter repeated and a before b before c?
• How many 5-letter words can be made from a,a,a,d,e?

Take Notice

The answer will be the same.

Jiaojiao’s solution:

$$5*4 = 20$$

and for the second question, we just consider the d and e, and it’s equivalent to the first question.

My stupid and slow solution:

Hence 2*10 = 20

Product rule: Symmetries and duplications

$$S_1 = \{\text{ accounting for symmetry }\}, \\ S_2 = \{ \text{ symmetries }\}, \\ S =\{\text{ sequences without symmetry }\}$$ $$S =S_1×S_2,$$

so

$$∣S1∣ = ∣S∣/∣S2∣$$

Alternatively, $\frac{1}{∣S_2∣}$ of the $∣S∣$ sequences meet the symmetric constraint.

Example

Question. Let Σ = {a,b,c,d,e}. How many 5-letter words with no letter repeated and a before b before c?

Answer

Let Σ′ = {a,b,c}. Then

$$∣S∣ = ∣\{\text{ 5 letter words using letters from Σ with no repeats }\}∣ \\ = \prod^4_{i=0}(∣Σ∣ −i) = 5⋅4⋅3⋅2⋅1 = 120$$

and

$$∣S_2∣ = ∣\{ \text{ orderings of elements in Σ′ }\}∣ \\ = \prod^2_{i=0}(∣Σ′∣ −i)= 3⋅2⋅1 = 6$$

So

$$∣S_1∣ = ∣\{ \text{ words in S containing a,b,c in order }\}∣ = \frac{120}{6} = 20$$

Combinations and Permutations

Combinatorial Objects: How Many?

permutations

Ordering of all objects from a set S; equivalently: Selecting all objects while recognising the order of selection.

The number of permutations of n elements is

$$n! = n⋅(n−1) ... 1, \\ 0! =1! =1$$

r-permutations (sequences without repetition)

Selecting any r objects from a set S of size n without repetition while recognising the order of selection.

Their number is

$$(n)_r = {}^n P_r = n⋅(n−1)⋯(n−r +1) = \frac{n!}{(n-r)!}$$

Permutations with duplicates

Example 1

Q: How many anagrams of ASSESS? Namely $\Sigma$={A,S,S,E,S,S}, and what is the number to permutate them?

A:

Label S’s: $AS_1S_2ES_3S_4: 6!$

In each anagram we can label the S’s in 4! ways.

Suppose there are m anagrams. So $m ⋅4!=6!$, i.e. $m=\frac{6!}{4!}$

Example 2

Number of anagrams of MISSISSIPPI?

$$\frac{11!}{4!4!2!}$$

r-selections (or: r-combinations)

Collecting any r distinct objects without repetition; equivalently: selecting r objects from a set S of size n and not recognising the order of selection.

$$\binom{n}{r} = \frac{(n)_r}{r!} = \frac{n!}{(n-r)!r!} = \frac{n(n-1)...(n-r+1)}{1 \cdot 2 \dots r}$$

Take Notice

These numbers are usually called binomial coefficients due to

$$(a+b)^n = a^n + \binom{n}{1}a^{n-1}b + \binom{n}{2}a^{n-2}b^{2} + \dots + b^n = \Sigma^n_{i=0} \binom{n}{i}a^{n-i}b^i$$

Also defined for any $\alpha \in \mathbb{R}$ as $\binom{\alpha}{r}=\frac{\alpha(\alpha-1)…(\alpha-r+1)}{r!}$

Simple Counting Problems

Give an example of acounting problem whose answer is

(a) $(26)_{10}$

(b) $\binom{26}{10}$

Draw 10 cards from a half deck (eg. black cards only)

(a) the cards are recorded in the order of appearance

(b) only the complete draw is recorded

---

Examples

Number of diagonals in a convex polygon

Number of poker hands

Decisions in games, lotteries etc.

Exercises: choose to from committees

From a group of 12 men and 16 women, how many committees can be chosen consisting of

(a) 7 members?

$\binom{12+16}{7}$

(b) 3 men and 4 women?

$\binom{12}{3}\binom{16}{4}$

(c) 7 women or 7 men?

$\binom{12}{7} + \binom{16}{7}$

As above,but any 4 people (male or female) out of 9 and two, Alice and Bob, unwilling to serve on the same committee.

Method 1:

Firstly, choose 4 people from 9 people. Secondly, consider Alice and Bob are in one committee, so 7 people remained, choose 2 more people from these 7 people, and could form a committee with Alice and Bob.

$${all committees} − {committees with both A and B} = \binom{9}{4} - \binom{7}{2} = 126 −21 = 105$$

Method 2:

equivalently, {A in, B out} + {A out, B in} + {none in} = $\binom{7}{3}+\binom{7}{3}+\binom{7}{4}$ = 35 +35+35 = 105

Exercises:Counting Poker Hands

A poker hand consists of 5 cards drawn without replacement from a standard deck of 52 cards

{A,2-10,J,Q,K} ×{club ♣,spade ♠,heart ♥,diamond ♦}

(a) Number of “4 of a kind” hands (e.g. 4 Jacks)

∣rank of the 4-of-a-kind∣ ⋅ ∣any other card∣ = 13 ⋅ (52 − 4)

这里问的是几种组合，所以13是A->K的同点数之一，然后因为一手5个牌还差一个，因此从(52-4)中随便选一个牌。

(b) Number of non-straight flushes, i.e. all ards of same suit but not consecutive (e.g. 8,9,10,J,K)

∣all flush∣ − ∣straight flush∣ = ∣suit∣⋅∣5-hand in a given suit∣ − ∣suit∣ ⋅ ∣rank of a straight flush in a given suit∣ = $4 \cdot \binom{13}{5} - 4 \cdot 10$

在问非顺子但同花的组合，4个花色乘13（同花）中抽5张（同花牌的数量），减去顺子同花：这种情况有10种可能的顺子（从 A, 2, 3, 4, 5 到 10, J, Q, K, A），因此顺子同花是$4 \cdot 10$. 故最终结果是以上两项相减。

注意，A在“A2345”和“10 JQKA”都可以是同花顺，所以同花情况下，应该是10个情况而不是9个情况。

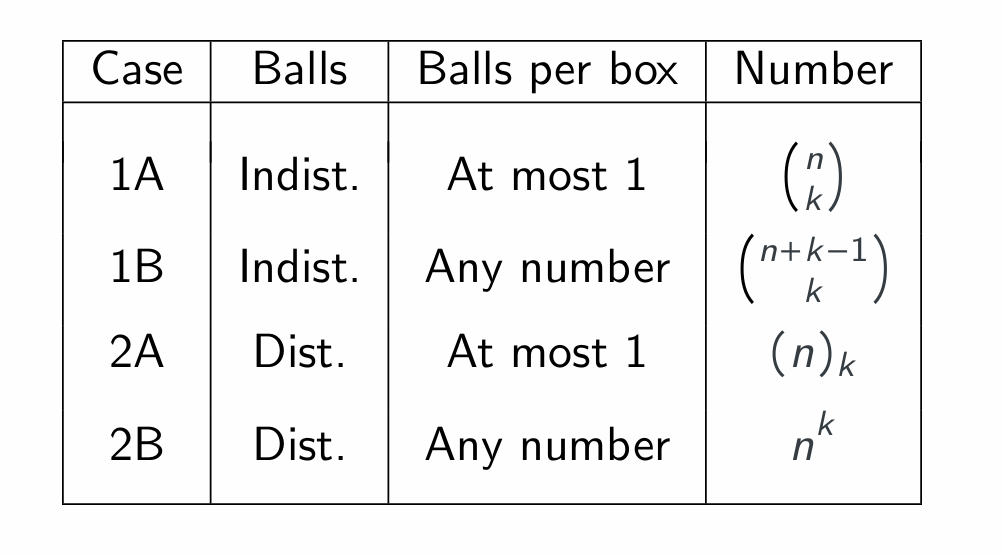
Summary

“Balls in boxes”

Have n “distinguishable” boxes.

Have k balls which are either:

1. Indistinguishable
2. Distinguishable

How many ways to place balls in boxes with

1. At most one
2. Any number of
   balls per box

Take Notice

Suppose K is a set with $∣K∣ = k$ and N is a set with $∣N∣ = n$:

• 2A counts the number of injective functions from K to N
• 2B counts the number of functions from K to N

Alternative Techniques

What if the current techniques are unwieldy?
Other techniques for obtaining an exact count:

• Find a different approach for counting
• Make use of symmetries
• Make use of recursion
• Write a program (running time?)

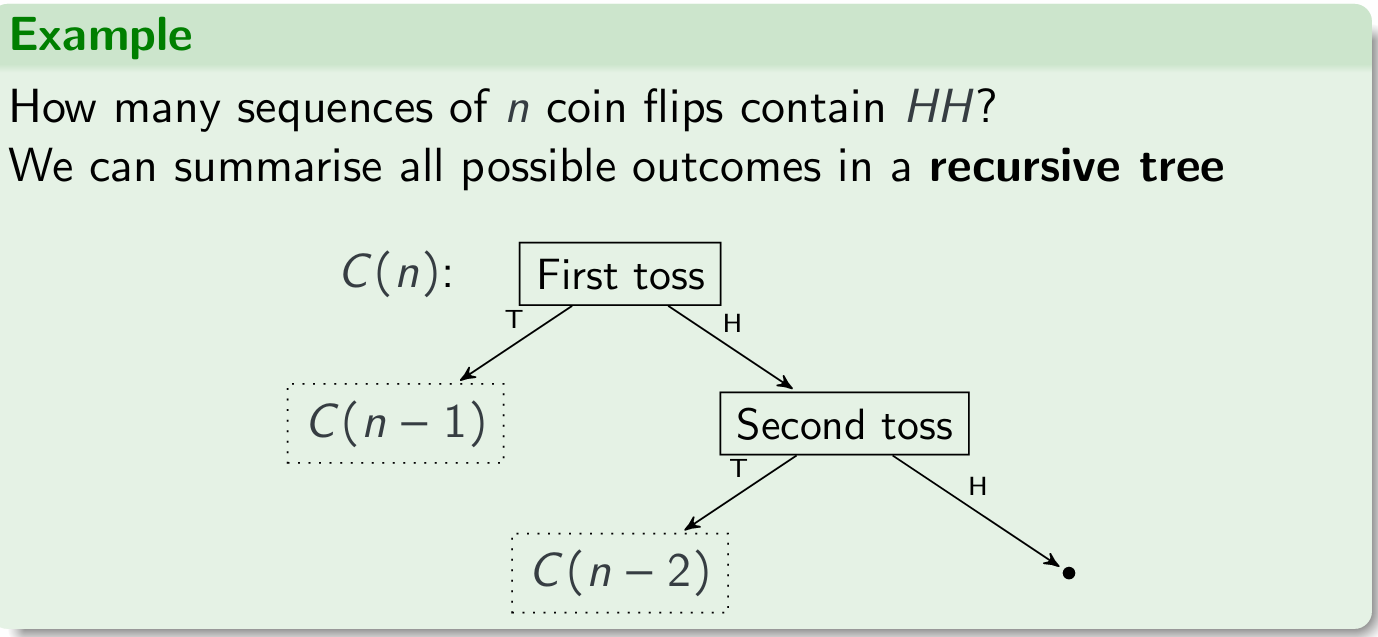
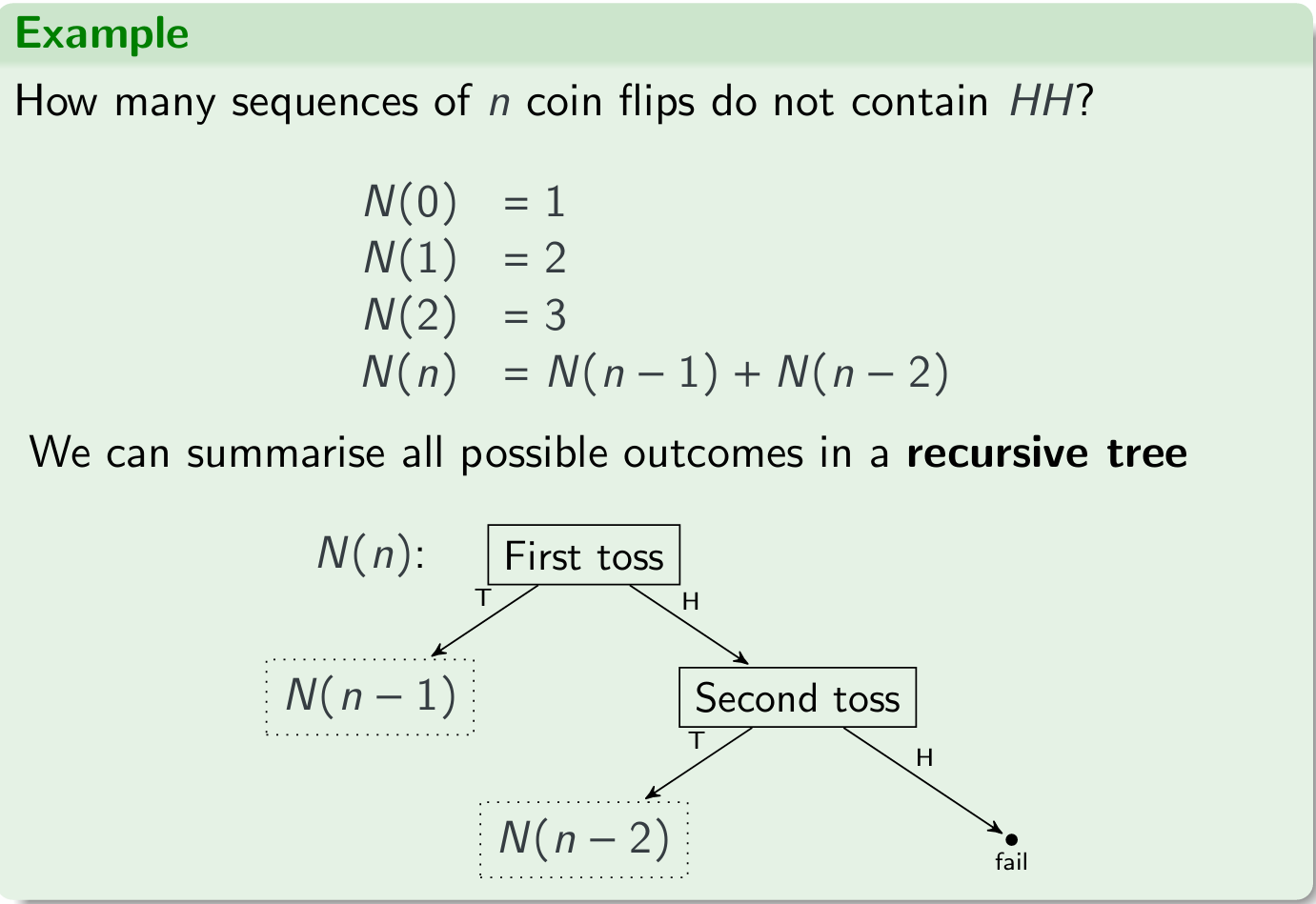
Example

How many sequences of 15 coin flips have an even number of heads?

Difficult Counting Problems (not assessed)

Using Programs to Count

Two dice, a red die and a black die, are rolled.
(Note: one die, two or more dice)

Write a program to list all the pairs {(R,B) ∶ R > B}

Similarly, for three dice, list all triples R > B > G

Generally, for n dice, all of which are m-sided (n ≤ m), list all decreasing n-tuples

Take Notice

In order to just find the number of such n-tuples, it is not
necessary to list them all. One can write a recurrence relation for
these numbers and compute (or try to solve) it.

Approximate Counting

---

Welcome to point out the mistakes and faults!