PREFACE

Lecture 14: Probability

• Elementary Discrete Probability
  • Definition
    • Examples
  • Uniform distribution
    • Examples
  • Computing Probabilities by Counting
  • Combining events
  • Inclusion-exclusion rule
    • Exercises
  • Examples
  • Exercises 1
  • Exercises 2
• Independence
  • Unifying sets of outcomes
  • Events in the product space
  • Probability in the product space
  • Product distribution
  • Independence
  • Independence of multiple events
  • Example: Dependent events
  • Exercise
  • Example: Sequences of independent events
  • Binomial distribution
    • exercise: die
    • exercise: die 2
    • exercise: ball
• Infinite Sample Spaces (not examinable)
• Recursive Probability Computations
  • Use of Recursion in Probability Computations
    • 1. gain T.
    • 2. gain H.
    • combine
• Conditional Probability
  • Definition
  • Conditional probability in uniform distributions
  • Some General Rules
    • example 1
    • example 2
    • example 3
    • example 4
• Independence, revisited — Stochastic Independence, again
  • Definition
  • exercise 1
  • exercise 2
  • exercise 3

Elementary Discrete Probability

Definition

Sample space:

$$\Omega = \{ w_1, \dots, w_n \}$$

Each point represents an outcome. 样本空间：包含所有可能结果的集合。

Event: a collection of outcomes = subset of $Ω$. 事件，是样本空间的一个子集。

Probability distribution: A function P : $Pow(\Omega)→ [0,1]$ （概率分布，定义了每个事件发生的概率。Pow是幂集，意思是所有的子集。）such that:

• $P(Ω) = 1$
• $E$ and $F$ disjoint events then $P(E ∪F) = P(E)+P(F)$.

Fact

$$P(∅) = 0, P(E^c) = 1−P(E)$$

Examples

Tossing a coin: Ω = {H,T}

$$P(H) = P(T) =0.5$$

Rolling a die: Ω = {1,2,3,4,5,6}

$$P(1) = P(2) = P(3) = P(4) = P(5) = P(6) = \frac{1}{6}$$

Uniform distribution

Each outcome $ω_i$ equally likely:

$$P(w_1)=P(w_2)= \dots =P(w_n)= \frac{1}{n}$$

This a called a uniform probability distribution over $Ω$

Examples

Tossing a coin: Ω = {H,T}

$$P(H) = P(T) =0.5$$

Rolling a die: Ω = {1,2,3,4,5,6}

$$P(1) = P(2) = P(3) = P(4) = P(5) = P(6) = \frac{1}{6}$$

Computing Probabilities by Counting

Computing probabilities with respect to a uniform distribution comes down to counting the size of the event.

If E = {$e_1$,…,$e_k$} then

$$P(E) = \Sigma^k_{i=1} P(e_i) = \Sigma^k_{i=1} \frac{1}{|\Omega|} = \frac{|E|}{|\Omega|}$$

Most of the counting rules carry over to probabilities wrt. a uniform distribution.

Important!

The expression “selected at random”, when not further qualified, means:

“subject to/according to/…a uniform distribution.”

Combining events

We can create complex events by combining simpler ones.

Common constructions:

• A and B: $A∩B$

• A or B: $A∪B$

• Not A: $Ω \setminus A$

• A followed by B

The first three involve events from the same set of outcomes. The last may involve events from different sets of outcomes (e.g. roll die and flip coin).

Inclusion-exclusion rule

Fact

$$P(A∪B) = P(A)+P(B)−P(A∩B) \\ P(A∪B ∪C) = P(A)+P(B)+P(C) −P(A∩B)−P(B ∩C)−P(C ∩A) +P(A∩B ∩C)$$

Exercises

Suppose an experiment leads to events A,B with probabilities $P(A) = 0.5,P(B) = 0.8,P(A ∩ B) = 0.4$.

Find

• $P(B^c)$
• $P(A∪B)$
• $P(A^c ∪B^c)$

$1 −P(B) =0.2$

$P(A) +P(B)−P(A∩B) =0.9$

$1 −P((A^c ∪B^c)^c) = 1−P(A∩B) =0.6$

You could draw a venn diagram, and found it’s the intersection between A and B.

---

Given $P(A)=0.6$, $P(B)=0.7$, show $P(A∩B)≥0.3$

$$P(A∩B) =P(A)+P(B)−P(A∪B) \\ =0.6+0.7−P(A∪B) \\ ≥0.6+0.7−1 = 0.3$$

Examples

Question. A four-digit number n is selected at random (i.e. randomly from [1000,…,9999]). Find the probability p that n has all of 0, 1, 2 among its digits.

Answer (approach). Let $q = 1−p$ be the complementary probability and define

$$A_i = \{n : \text{ no digit } i\},A_{ij} = \{n : \text{ no digits } i,j\},A_{ijk} = \{n : no \quad i,j,k\}$$

Then define

$T =A_0∪A_1∪A_2 =${n: missing at least one of 0,1,2}

$S =(A_0∪A_1∪A_2)^c =${n : containing all of 0,1,2}

Once we find the cardinality of T, the solution is

$$q = \frac{|T|}{9000}, p = 1-q$$

To find $|Ai|,|A{ij}|,|A_{ijk}|$ we reflect on how many choices are available for the first digit, for the second etc. A special case is the leading digit, which must be 1,…,9

Answer (arithmetic).

$$|A_0|=9^4, |A_1| = |A_2| = 8 \cdot 9^3 \\ |A_{01}| = |A_{02}| = 8^4, \\ |A_{12}| = 7 \cdot 8^3, |A_{012}| = 7^4, \\ |T| = |A_0 ∪A_1 ∪A_2| \\ = |A_0| +|A_1|+|A_2|−|A_0 ∩A_1|−|A_0 ∩A_2|−|A_1 ∩A_2| \\ +|A_0 ∩A_1 ∩A_2| \\ =9^4 +2·8·9^3 −2·8^4 −7·8^3 +7^4 \\ =25·9^3 −23·8^3 +7^4 = 8850$$

Hence

$$q=\frac{8850}{9000}, p =1−q \approx 0.01667$$

Previous example generalised: Probability of an r-digit number having all of 0,1,2,3 among its digits.

We use the previous notation: $Ai$ — set of numbers n missing digit i, and similarly for all $A{ij}$…

We aim to find the size of $T = A_0 ∪A_1 ∪A_2 ∪A_3$, and then to compute $|S| = 9·10^{r−1} −|T|$.

$$|A_0 ∪A_1 ∪A_2 ∪A_3| = sum of |A_i| \\ − sum of |A_i ∩A_j| \\ + sum of |A_i ∩A_j ∩A_k| \\ − sum of |A_i ∩A_j ∩A_k ∩A_l|$$

Exercises 1

(Supp) Of 100 problems, 75 are ‘easy’ and 40 ‘important’.

(b) n problems chosen randomly. What is the probability that all n are important?

$$p=\frac{\binom{40}{n}}{\binom{100}{n}}$$

Exercises 2

A 4-letter word is selected at random from $Σ^4$,where Σ={a,b,c,d,e}. What is the probability that

(a) the letters in the word are all distinct?

$$|E| = (5)_4, P(E)=\frac{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{(5-4)! \cdot 5^4} = \frac{120}{625} \approx 19\%$$

(b) there are no vowels (“a”,“e”) in the word?

$$|E| = 3^4, P(E)=\frac{3^4}{5^4}=\frac{81}{625} \approx 13\%$$

(c) the word begins with a vowel?

$$|E| = 2·5^3, P(E) = \frac{2·5^3}{5^4} = \frac{2}{5}$$

Independence

Unifying sets of outcomes

To combine events from different sets of outcomes we unify the sample space using the product space: $\Omega_1 \times \Omega_2 \times \dots \times \Omega_n$

Example

Flipping a coin and rolling a die:

Ω1 ={heads,tails}

Ω2 ={1,2,3,4,5,6}

Ω=Ω1×Ω2 ={(heads,1),(heads,2),…}

Take Notice

This approach can also be used to model sequences of outcomes.

Events in the product space

Events are lifted into the product space by restricting the appropriate co-ordinate. E.g. $A ⊆ Ω_1$ translates to $A′ = A×Ω_2×…×Ω_n$

Example

Coin shows heads and die shows an even number:

Ω1 ={heads,tails}

A ={heads}

Ω2 ={1,2,3,4,5,6}

B ={2,4,6}

$$Ω=Ω1×Ω2 =\{(heads,1),(heads,2),...\}$$ $$A′ = A×Ω_2 \quad B′=Ω_1×B$$

“A and B” or “A followed by B” corresponds to:

$$A′ ∩B′ = (A×Ω2)∩(Ω1×B)=A×B$$

Probability in the product space

Take Notice

Cannot assume that $P(A ×B) = P(A)P(B)$

这里乍一看有点问题，因为明显A’和B’有个交集。图中表示第一枚硬币和第二枚硬币的方式，不应该如图中去写这个元组和集合。

首先考虑顺序，肯定用元组，但是要用(HH), (HT)就行，但是可以说无法直接找到符合情况的例子。

但是图中这里是说，(H,TT)是个空集实际上。

Product distribution

Given probability distributions on the component spaces, there is a natural probability distribution on the product space:

$$P(E_1 ×E_2 ×...×E_n) = P_1(E_1)·P_2(E_2)···P_n(E_n)$$

Intuitively, the probability of an event in one dimension is not affected by the outcomes in the other dimensions.

Fact

If the $P_i$ are uniform distributions then so is the product distribution.

Independence

Informally, events are independent if the outcomes in one do not affect the outcomes in the other.

More generally, we define independence on events of the same sample space.

Definition

A and B are (stochastically) independent (notation: $A⊥B$) if $P(A∩B) =P(A)·P(B)$

Important!

Unless specified otherwise, we assume independence when unifying events (where appropriate).

Independence of multiple events

Independence of $A_1,…,A_n (A_1⊥A_2⊥···⊥A_n)$

$$P(A_1 ∩A_2 ∩...∩A_k) = P(A_1)·P(A_2)···P(A_k)$$

This is often called (for emphasis) a full independence

Pairwise independence is a weaker concept.

Example: Dependent events

Basic non-independent sets of events (assuming non-trivial probabilities)

• $A ⊆B$

• $A∩B =∅$

• Any pair of one-point events A = {x}, B = {y}: either x = y and $A ⊆ B$ or $x \neq y$ and $A∩B =∅$

Exercise

$⊥$ 在概率上表示独立事件。

Example: Sequences of independent events

(a)

(b)

(c)

这里我最开始对BO7获胜终止条件有疑惑，但是后来自己算了下和想了想，其实这里为什么赢了3盘就可以了(a)但还算赢4赢5赢6.因为如果第二第三第四盘赢了3盘，A队自动赢了已经，这就是$\binom{6}{3}$，剩下的盘数B都算自动输。$\binom{6}{4}$是说6个位置排4个组合，一个是A赢得3，一个是B赢得1，所以是$\binom{6}{4}$。

Binomial distribution

A useful corollary:

Fact

In a sequence of n ndependent trials, each with a probability of p of success:

$$P(exactly k successes) = \binom{n}{k} p^kq^{n-k}$$

where q = (1−p)

Take Notice

This leads to a probability distribution on sequences of outcomes, known as the binomial distribution.

比如BO7，赢得概率是固定的，但是第一把和第二把或者更多的盘，互相之间是独立的。所以遵从二项分布。

exercise: die

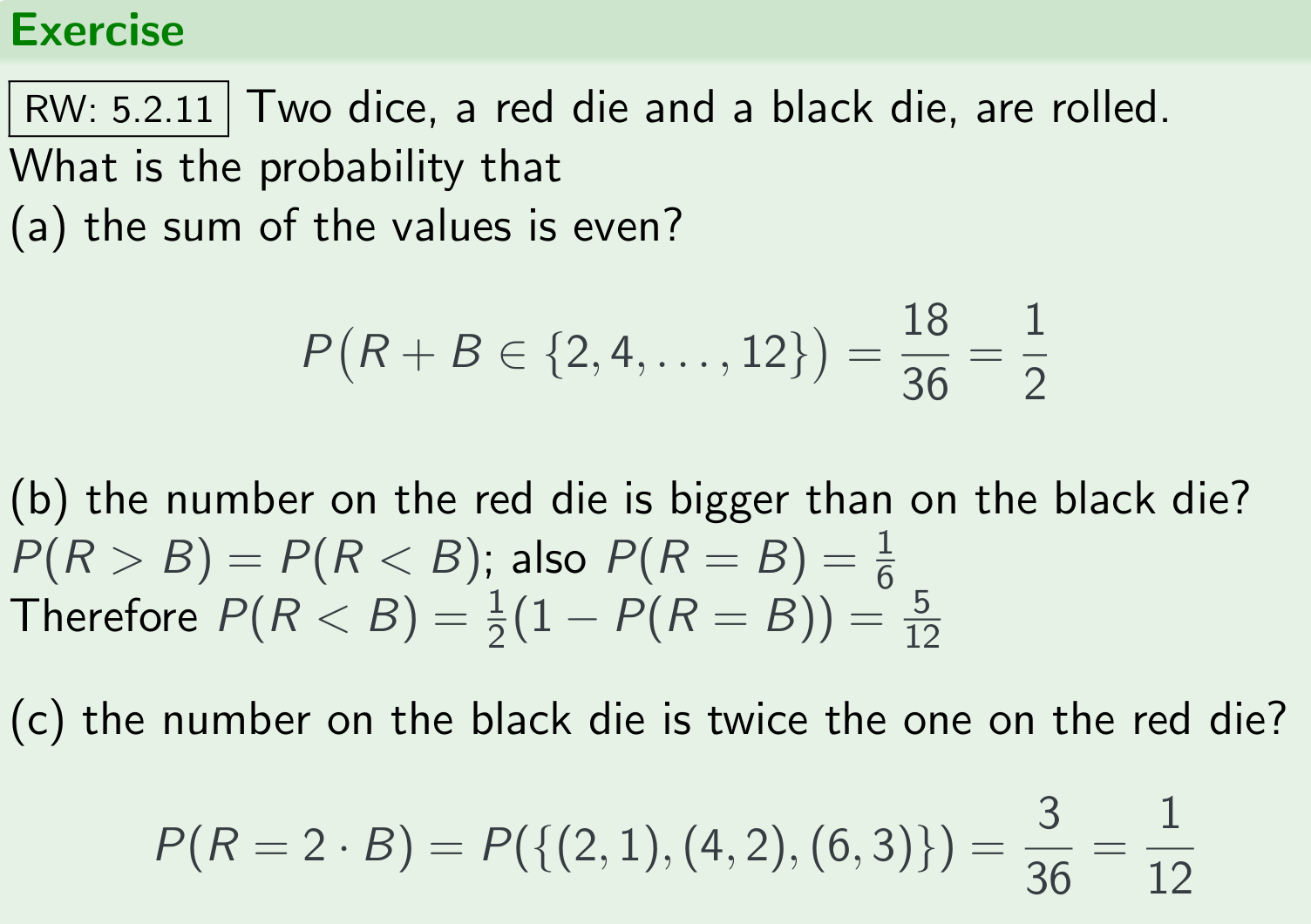
exercise: die 2

这个check比较精髓，(4,4)是交集。

exercise: ball

Infinite Sample Spaces (not examinable)

暂时先过这块儿，反正说是不考

Recursive Probability Computations

Use of Recursion in Probability Computations

问的是没有“HH”如果只抛

There are talking without successive HEAD “HH“.

Firstly, toss a coin for one time, then gain H or T. Both have no HH, so N(1)=2.

Secondly, toss a coin for two times, then gain HH HT TH TT. HH cannot hold, exclude it then we gain 3 legal sequences, so N(2)=3.

Thirdly, toss a coin for three times, then we would gain H or T in third time. Then classify its situations: (you can imagine 3rd as Nth time)

1. gain T.

Because Nth time we gain T, so we won’t worry about the H or T of the coin of (N-1) time. Hence, if gain T in Nth time, it would have (N-1)’s number of sequences. N(N) = N(N-1) iff Nth is T.

2. gain H.

If we want to gain without HH, hence it demands the result of the coin in (N-1) time cannot be H. So if Nth gain H, then (N-1)th must be T. Then (N-1) is T, so the number of the sequences will be (N-1)’s number of sequences. N(N) = N(N-2) iff Nth is H.

combine

Hence N(N) = N(N-1) + N(N-2), and N(1)=2 N(2)=3

(n)	1	2	3	4	5	6	7	8
—-	2	3	5	8	13	21	34	55
fabonacci	0	1	1	2	3	5	8	13
$\frac{1}{\sqrt{5}}(\frac{\sqrt{5}+1}{2})^{n+1}$	1	1	2	3	5	8	13	21

Conditional Probability

Definition

Conditional probability in uniform distributions

Some General Rules

example 1

example 2

example 3

example 4

Independence, revisited — Stochastic Independence, again

Definition

Using independence to simplify calculations

exercise 1

只要交集概率不是两者乘积，就说明不是互相独立

exercise 2

exercise 3

---

Welcome to point out the mistakes and faults!