Lecture 16: Graph Theory
- Motivation and Applications
- Terminology and Notation
- Graph Traversals
- Properties of Graphs
Motivation and Applications
Graph theory: Historical Motivation
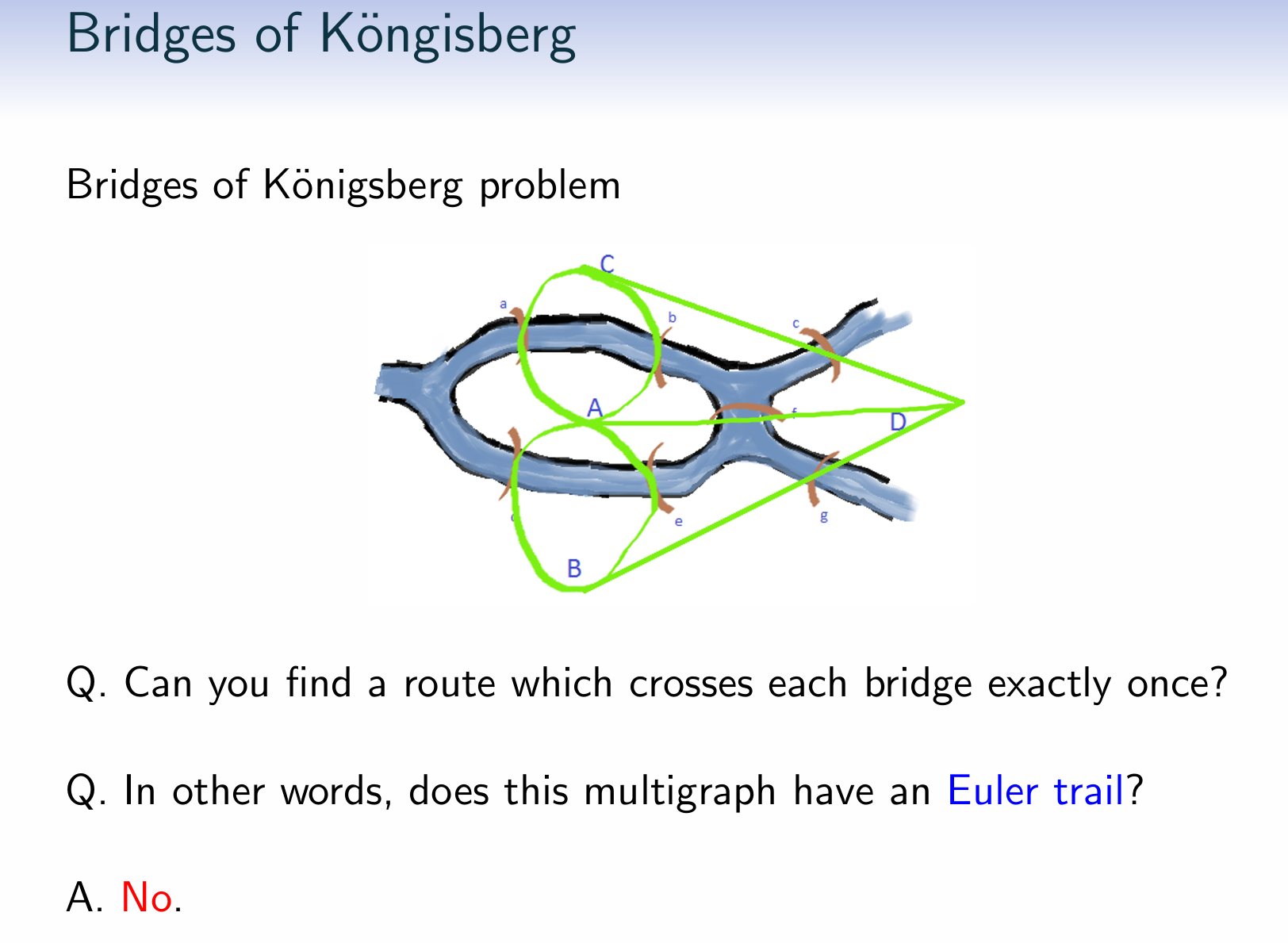
Bridges of K¨onigsberg problem
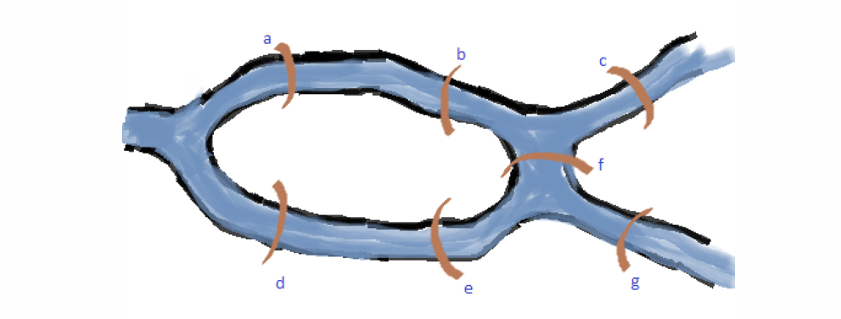
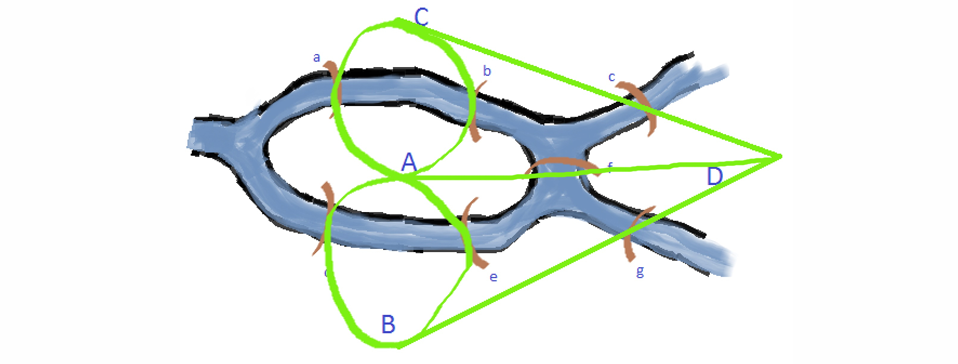
Can you find a route which crosses each bridge exactly once?
No! It doesn’t have such a solution.
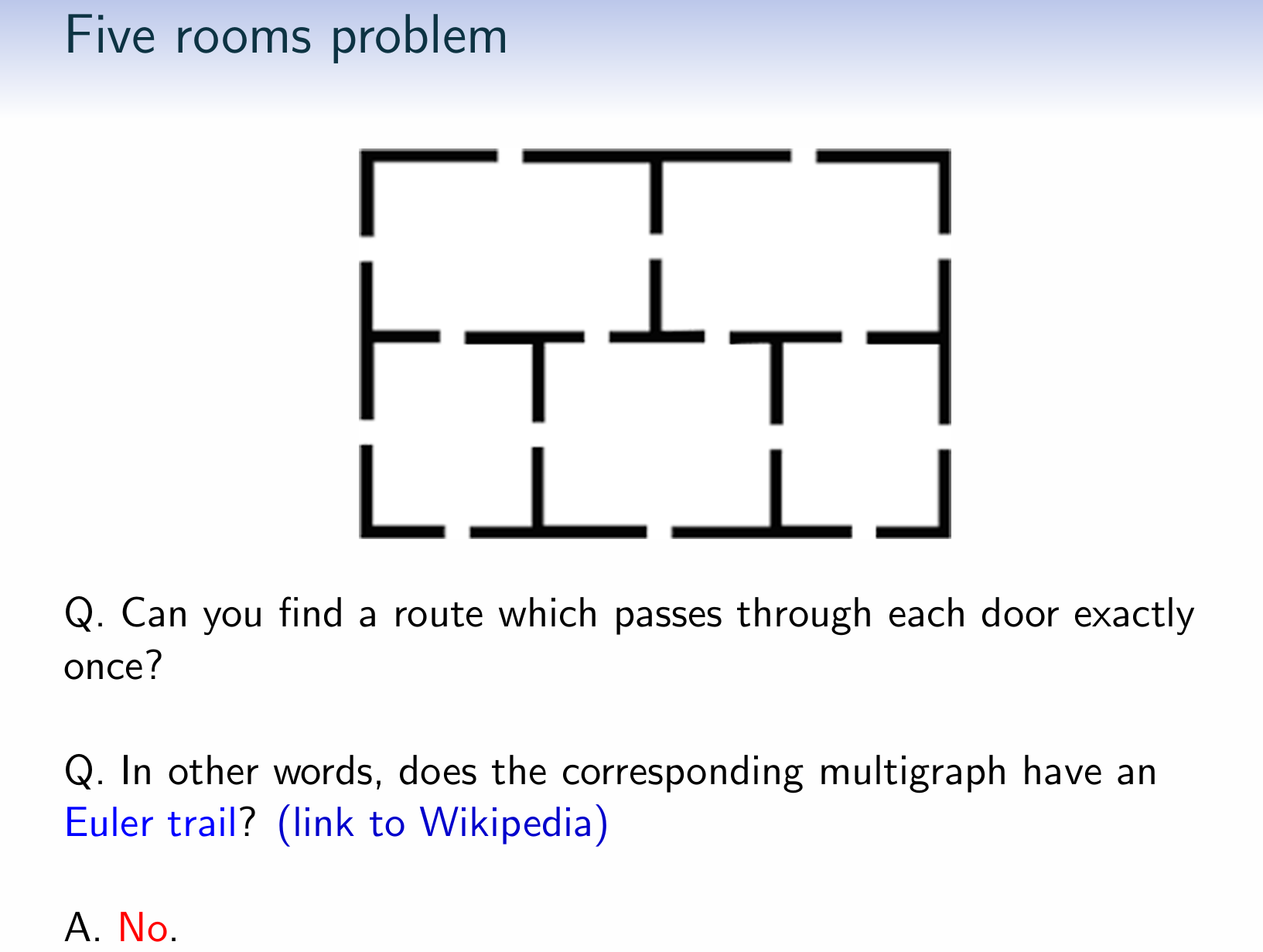
Five rooms problem
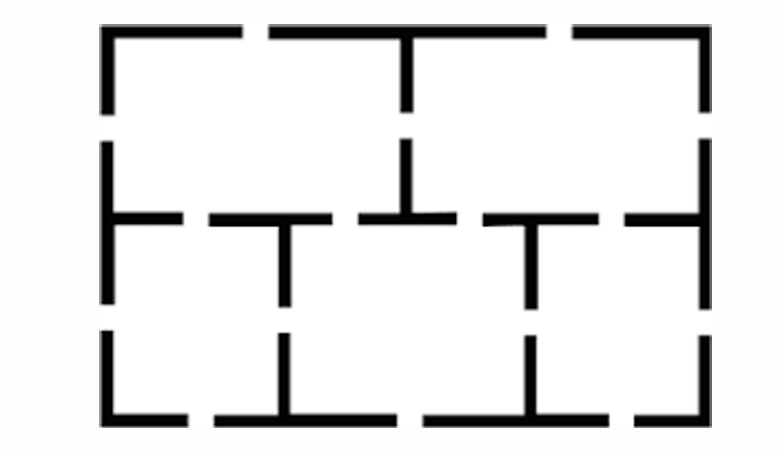
Can you find a route which passes through each door exactly once?
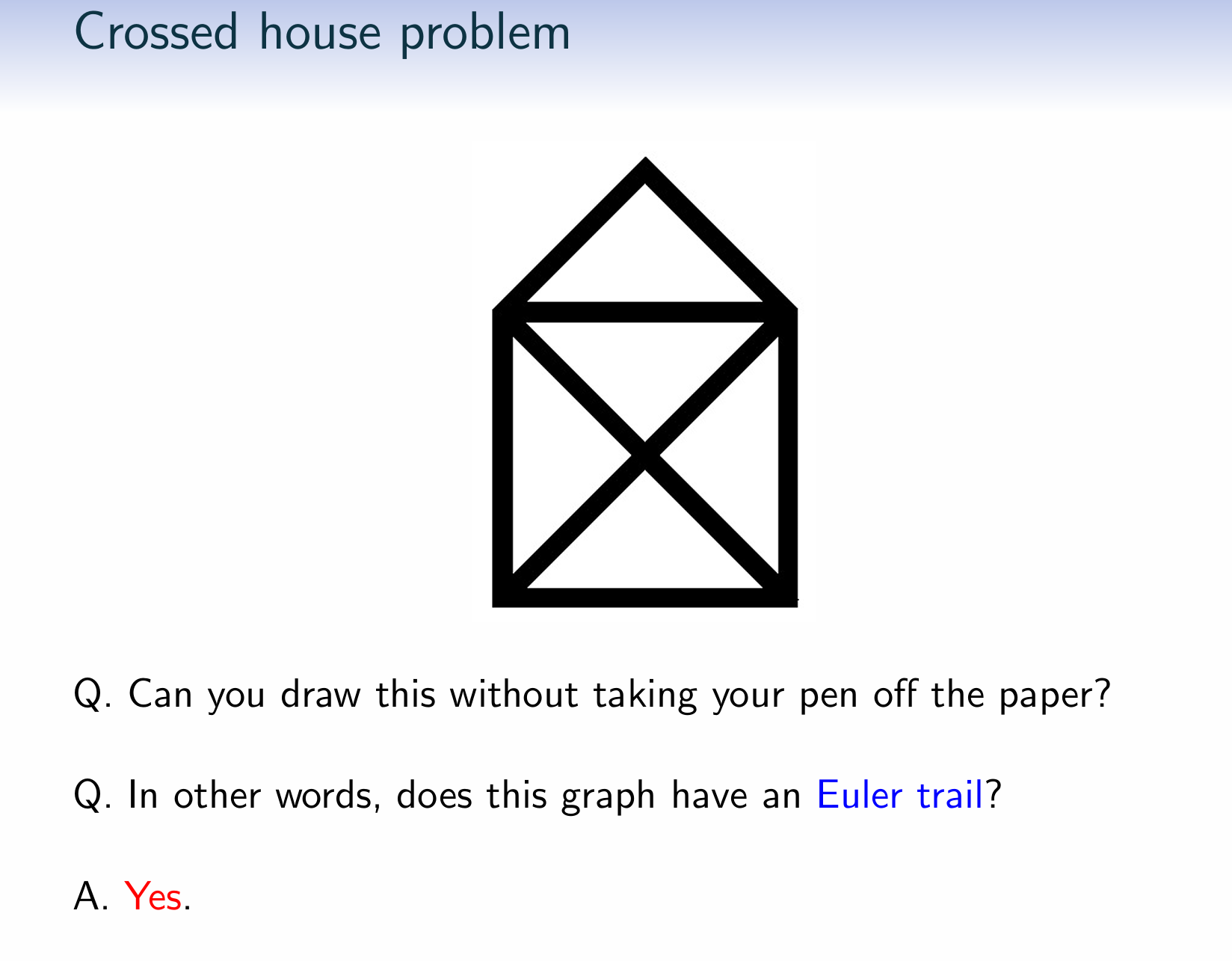
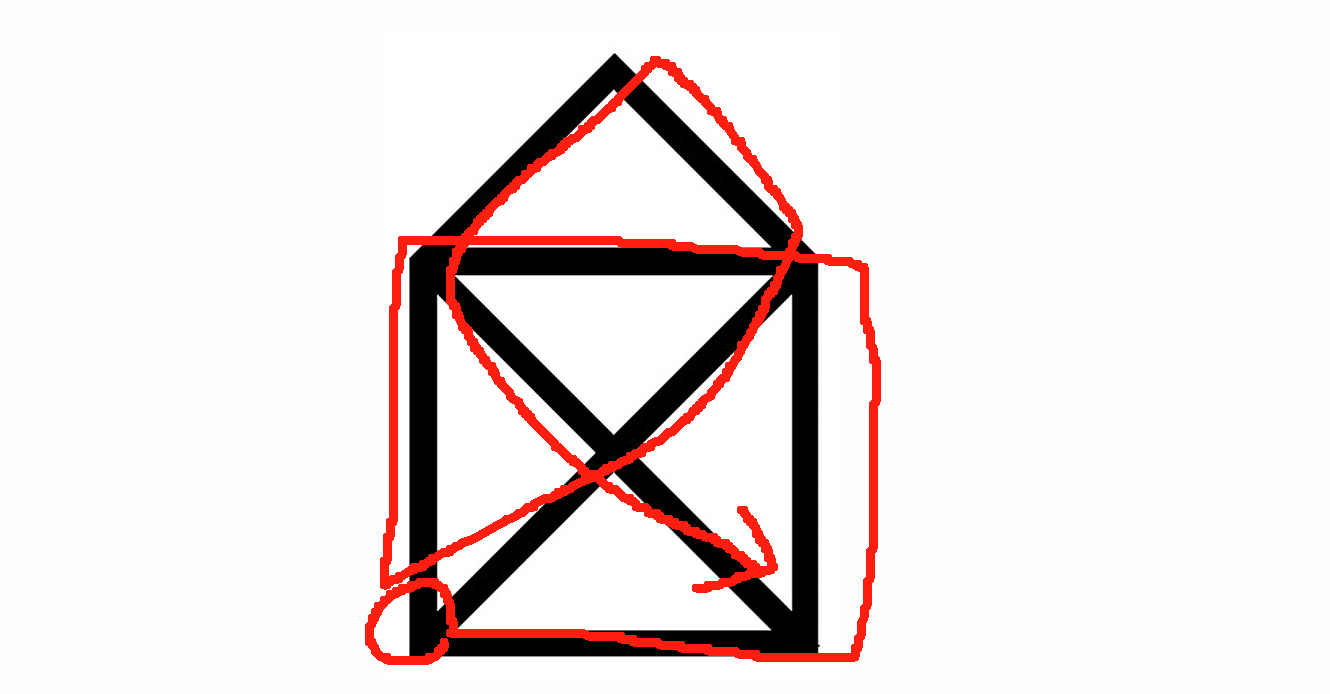
Crossed house problem

Can you draw this without taking your pen off the paper?
Three utilities problem

Can you connect all utilities to all houses without crossing connections?
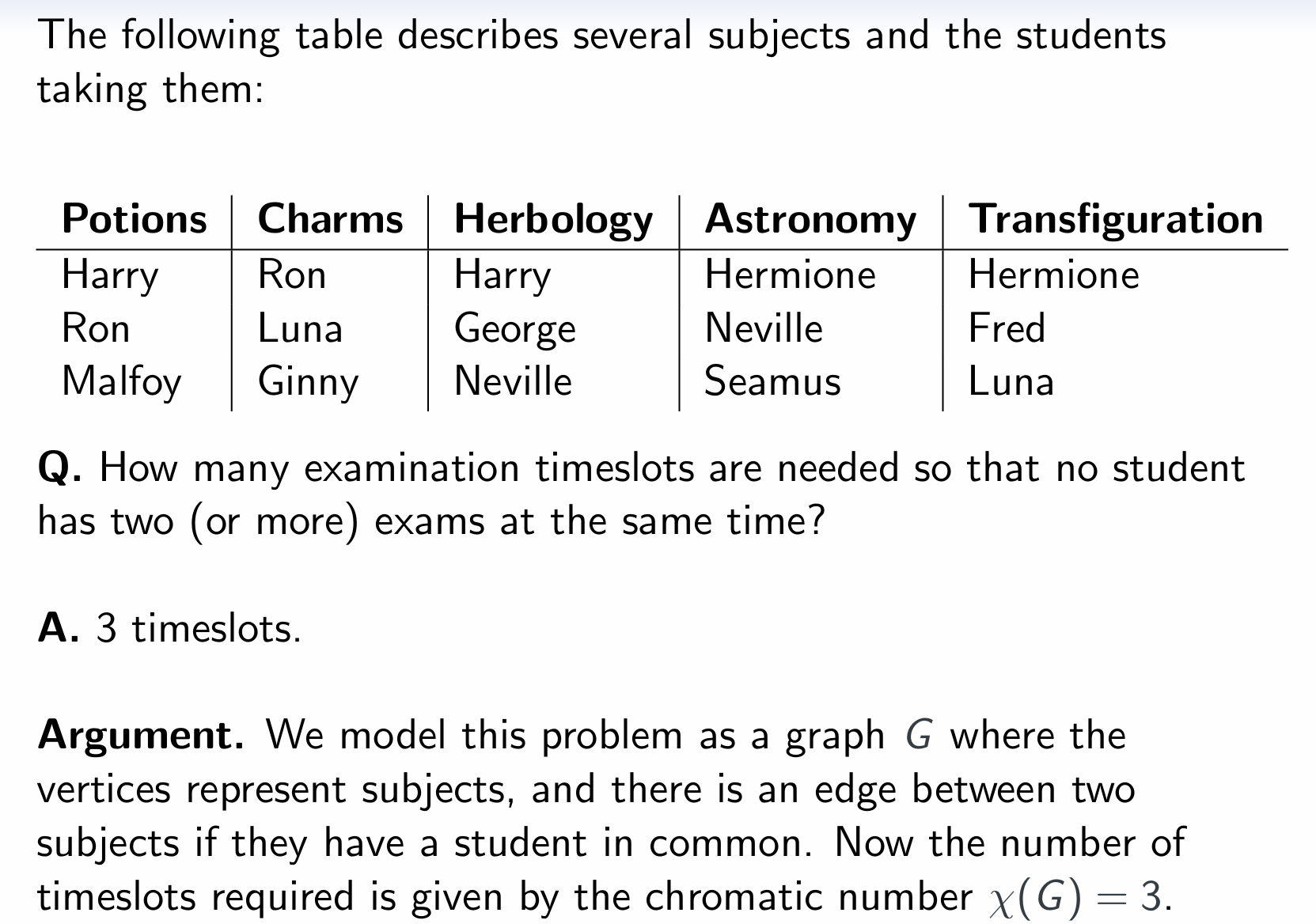
The following table describes several subjects and the students taking them:
| Potions | Charms | Herbology | Astronomy | Transfiguration |
|---|---|---|---|---|
| Harry | Ron | Harry | Hermione | Hermione |
| Ron | Luna | George | Neville | Fred |
| Malfoy | Ginny | Neville | Seamus | Luna |
How many examination timeslots are needed so that no student has two (or more) exams at the same time?
Graphs in Computer Science
Applications of graphs in Computer Science are abundant, e.g.
- route planning in navigation systems, robotics
- optimisation, e.g. timetables, utilisation of network structures, bandwidth allocation
- compilers using “graph colouring” to assign registers to program variables
- circuit layout (Untangle game)
- determining the significance of a web page (Google’s pagerank algorithm)
- modelling the spread of a virus in a computer network or news in social network
Terminology and Notation
Terminology (the most common; there are many variants):
Graph — pair (V,E) where V– set of vertices (or nodes) E– set of edges
Undirected graph: Every edge e ∈ E is a two-element set of vertices, i.e. e = {x,y} ⊆ V where x= y
Directed graph: Every edge (or arc) e ∈ E is an ordered pair of vertices, i.e. e = (x,y) ∈ V ×V, note x may equal y.
Graph representations
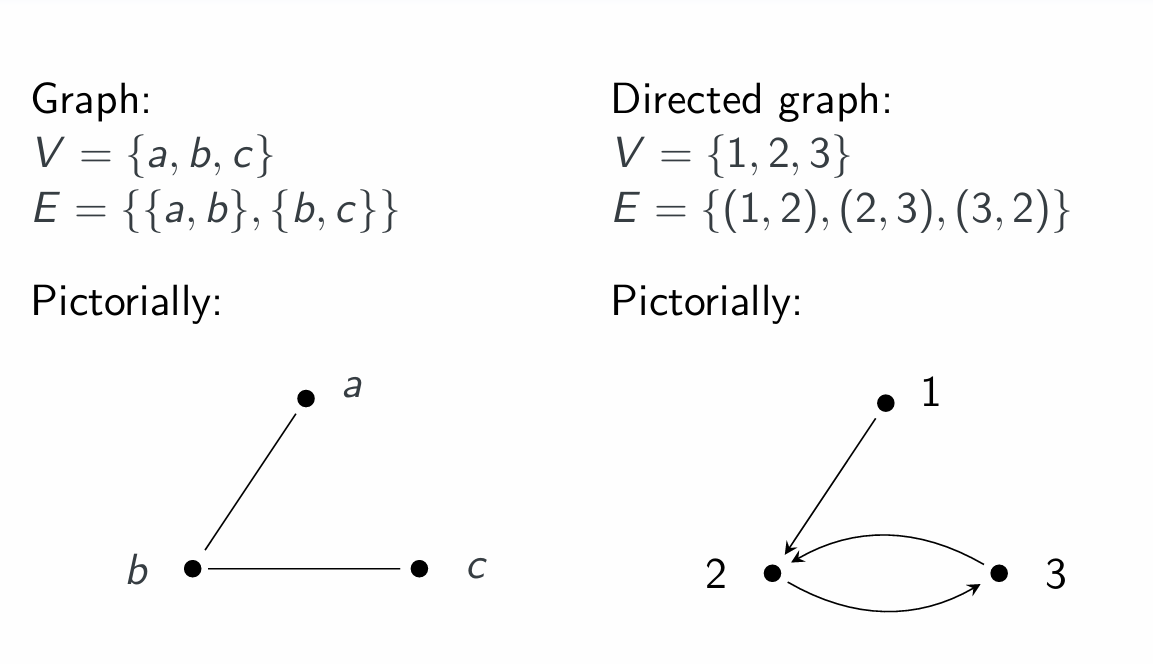



我对这个图的理解,无向图,横坐标是定点,纵坐标是那几个Edge;有向图,横纵坐标都是定点,纵射向横(好像不对),完了问问。
Paths
A (directed) walk in a (directed) graph (V,E) is a sequence of edges that link up
where $ei$ = {$v{i−1},vi$} ∈ $E (or \quad e_i = (v{i−1},v_i) ∈ E)$
A trail is a walk where no edge is repeated. $(∀i, j ∈ [n],e_i \neq e_j)$
trail过边,点重复
A path is a walk where no vertex is repeated $(∀i, j ∈$ {0,…n − 1}$,v_i \neq v_j)$
path过点,边重复
length of a walk is the number of edges: n neither the vertices nor the edges have to be all different
Subpath\subwalk of length $r: (em,e{m+1},…,e_{m+r−1})$
Path of length 0: single vertex $v_0$
Connectedness
Connected set/graph (undirected) — each pair of vertices joined by a path
Strongly connected set/graph (directed) — each pair of vertices joined by a directed path in both directions
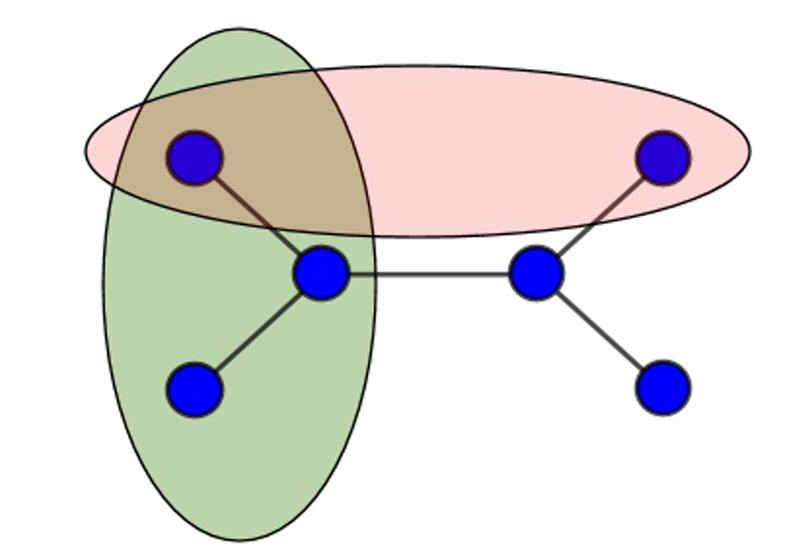
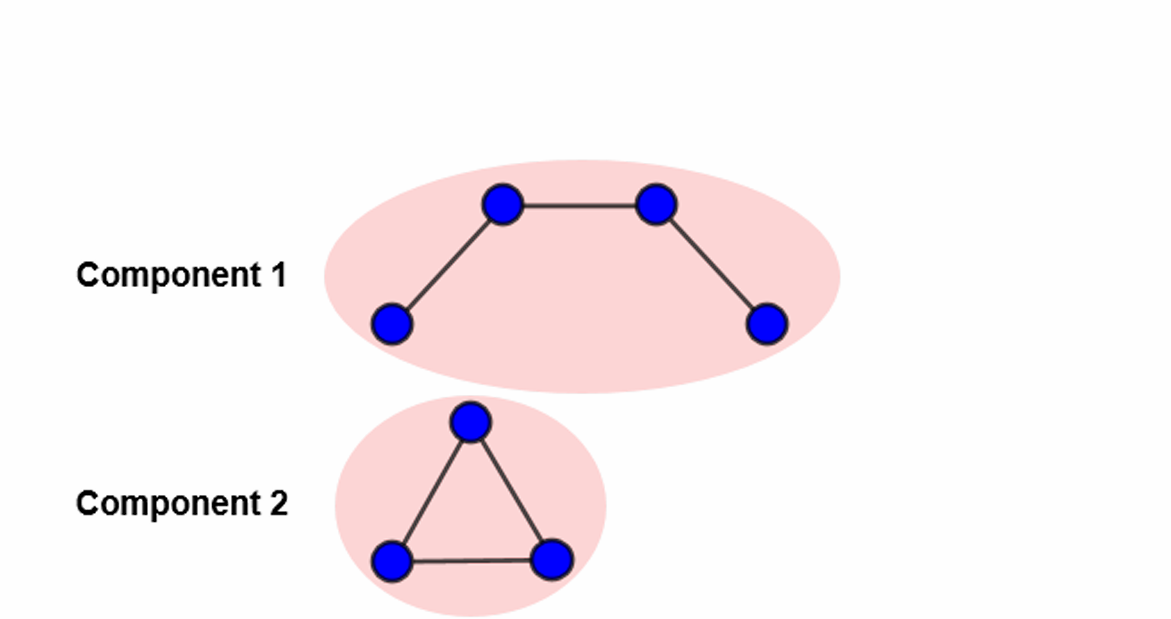
Given a graph $G = (V,E)$, we call a set of vertices $U ⊆ V$ a connected component of G, if every pair of vertices $u, v ∈ U$ is connected by some path, and $U$ is maximal with this property.

Vertex Degrees (Undirected graphs)
Degree of a vertex
i.e., the number of edges attached to the vertex
Regular graph — all degrees are equal
Degree sequence $D_0,D_1,D_2,…,D_k$ of graph $G = (V,E)$, where $D_i$ = no. of vertices of degree i
注意啊,这个下标,不是说第几个点的度数,是有几个度的点。
Question
What is $D_0 +D_1 +…+D_k$?
Fact
$\sum_{v \in V} deg(v) = 2·|E|$; so the sum of vertex degrees is always even.
Corollary
There is an even number of vertices of odd degree.
Vertex Degrees (Directed graphs)
Out-degree of a vertex
i.e., the number of edges going out of the vertex
In-degree of a vertex
i.e., the number of edges going in to the vertex
Fact
Exercise 1
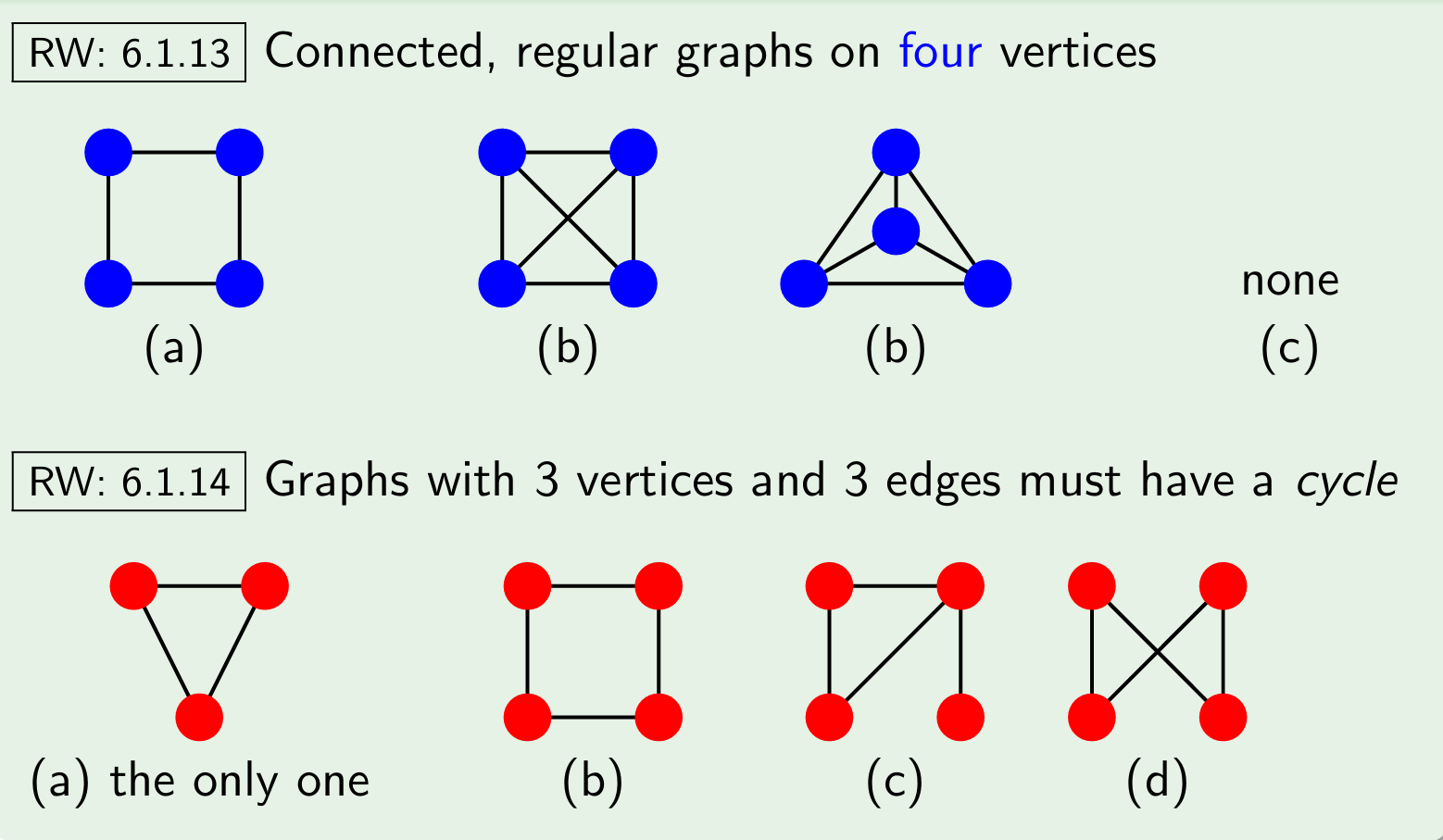
Draw a connected, regular graph on four vertices, each of degree 2
Draw a connected, regular graph on four vertices, each of degree 3
Draw a connected, regular graph on five vertices, each of degree 3
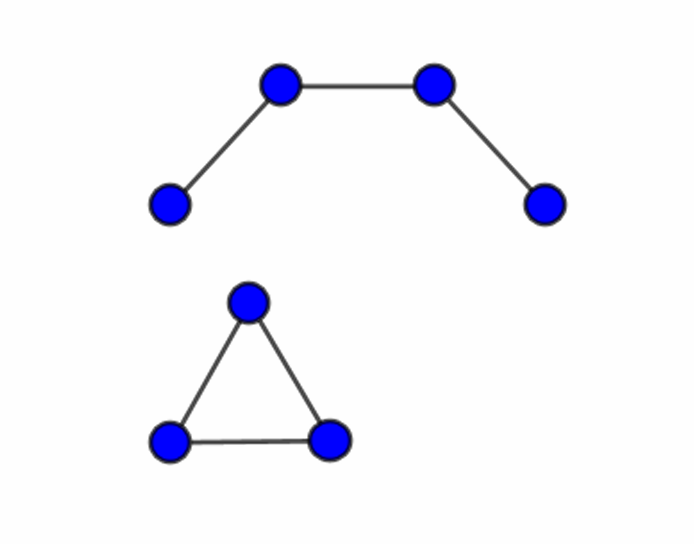
Graph with 3 vertices and 3 edges
Two graphs each with 4 vertices and 4 edges
Take Notice
We use the notation
$n =v(G) =|V|$ for the no. of vertices of graph $G = (V,E)$
$m=e(G)=|E|$ for the no. of edges of graph $G = (V,E)$
Exercise 2
Graph with $e(G)=21$ edges has a degree sequence $D_0 =0,D_1 =7,D_2 =3,D_3 =7,D_4 =$?
Find $v(G)$
$\sum{v} deg(v)= 2|E|$; here $7 · 1+3·2+7·3+x ·4=2·21$ giving $x = 2$, thus $v(G) = \sum{D_i} =19$.
How would your answer change, if at all, when $D_0 =6$?
No change to $D_4$; $v(G) = 25$.
算顶点时,勿忘加$D_0$ (度数为0的定点)
Cycles
Recall walks $v_0 \overset{e_1}{→} v_1 \overset{e_2}{→} … \overset{e_n}{→} v_n$
- closed walk — $v_0 = v_n$
意思是如果首尾同点,意味着首尾相连,就是封闭walk。
- cycle — closed walk of length 3 or more (2 or more in directed graphs) whose vertices are distinct except $v_0$ and $v_n$.
无向图至少三点,有向图至少两点。
- acyclic walk (equivalent to path) — $v_i \neq v_j$ for all vertices in the path $(i \neq j)$
Take Notice
$C =(e_1,…,e_n)$ is a cycle iff removing any single edge leaves a path.
C is a cycle if it has the same number of edges and vertices ($|V_G| = |E_G|$) and no proper subwalk has this property.
Trees
Acyclic graph — graph that doesn’t contain any cycle
Tree — connected acyclic [undirected] graph
A graph is acyclic iff it is a forest (collection of disjoint trees)
Take Notice
Graph G is a tree if
⇔ it is acyclic and $|V_G| = |E_G| +1$.
⇔ there is exactly one path between any two vertices.
⇔ G is connected, but becomes disconnected if any single edge is removed.
⇔ G is acyclic, but has a cycle if any single edge on already existing vertices is added.
Trees
A tree with one vertex designated as its root is called a rooted tree.
It imposes a direction on the edges: ‘away’ from the root — from parent nodes to children. It also defines a level number (or: depth) of a node as its distance from the root.
Another very common notion in Computer Science is that of a DAG —a directed, acyclic graph.
Exercise (Supplementary)
(Supp) Tree T with n vertices, $n ≥3$. Always true, false or could be either?
(a) e(T) $\overset{?}{=}$ n
False. V(T) = E(T) + 1
(b) at least one vertex of degree exactly 2?
Could be either

(c) at least two $v_1,v_2$ s.t. $deg(v_1)=deg(v_2)$
True
(d) exactly one path from $v_1$ to $v_2$
True (characterises a tree)
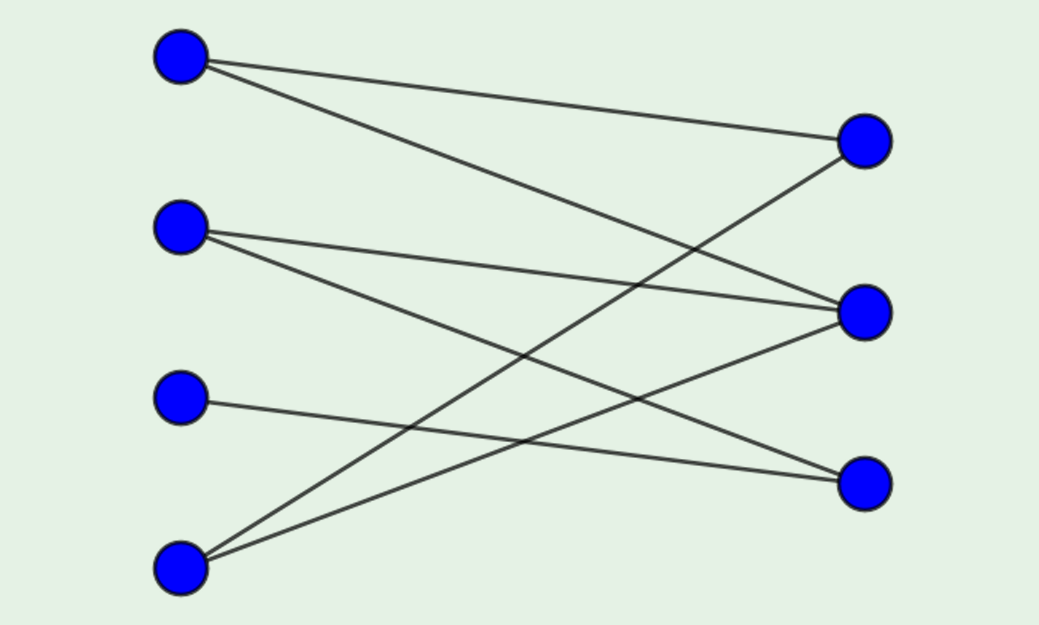
Bipartite Graphs
Can divide the vertices into two disjoint sets, $V = V_1 ∪ V_2$
Each edge must connect a vertex from $V_1$ to a vertex from $V_2$
Special Graphs
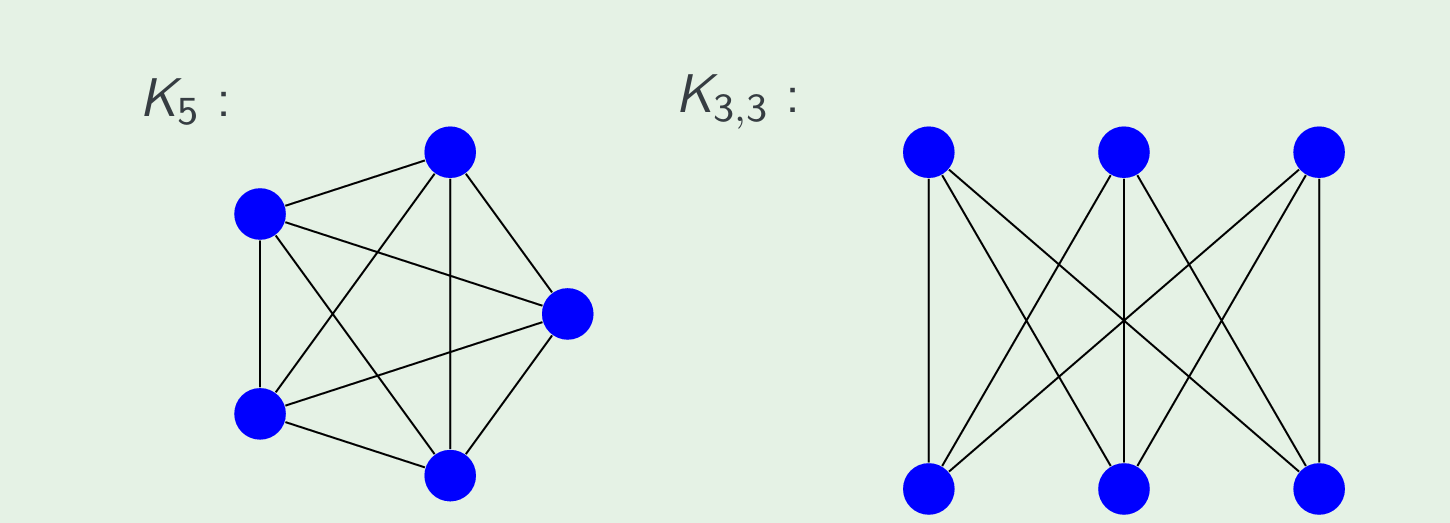
Complete graph $K_n$
n vertices, all pairwise connected, $\frac{n(n-1)}{2}$ edges.
Complete bipartite graph $K_{m,n}$
Has $m+n$ vertices, partitioned into two (disjoint) sets, one of n, the other of m vertices.
All vertices from different parts are connected; vertices from the same part are disconnected. No. of edges is $m · n$
Complete k-partite graph $K_{m_1,…,m_k}$
Has $m_1 +…+m_k$ vertices, partitioned into k disjoint sets, respectively of $m_1,m_2,…$ vertices.
No. of edges is $\sum{i<j}m_im_j = \frac{1}{2} \sum{i \neq j}m_im_j$
These graphs generalise the complete graphs
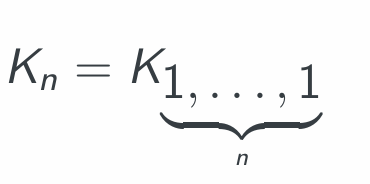
前面完全图是一个概念,后面俩 n分图 是一个概念。因为mi * mj (i不等于j是说不要自己搞完全图,因为这是k分图,没有reflexive)。因为axb 和 bxa是一会儿事儿,所以要除以2. 2分图的 mxj其实也是这个公式。
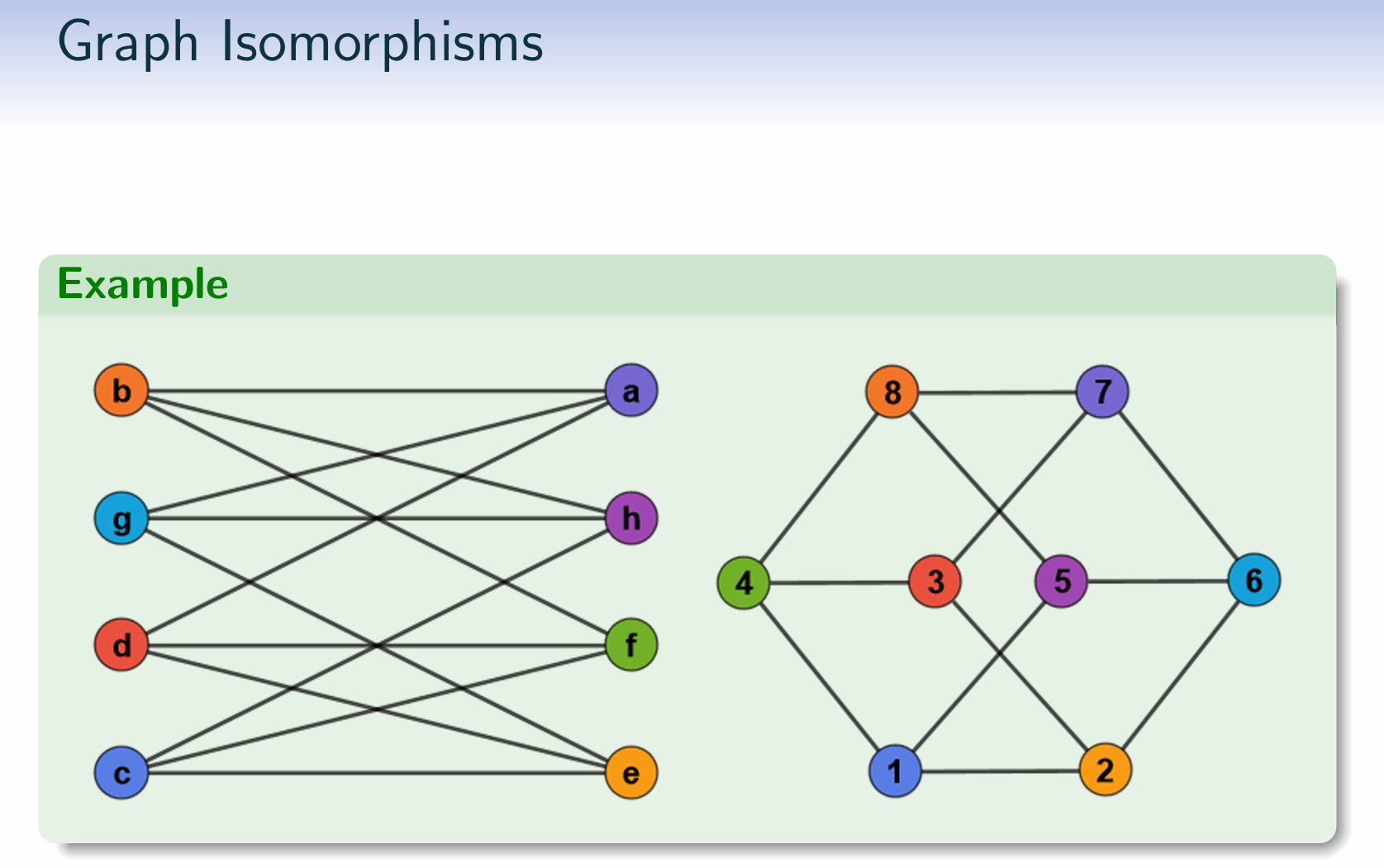
Graph Isomorphisms
$ϕ : G → H$ is a graph isomorphism if
$ϕ : V_G → V_H$ is a bijection
$(x,y) ∈ E_G$ iff $(ϕ(x),ϕ(y)) ∈ E_H$
Two graphs are called isomorphic if there exists (at least one) isomorphism between them.

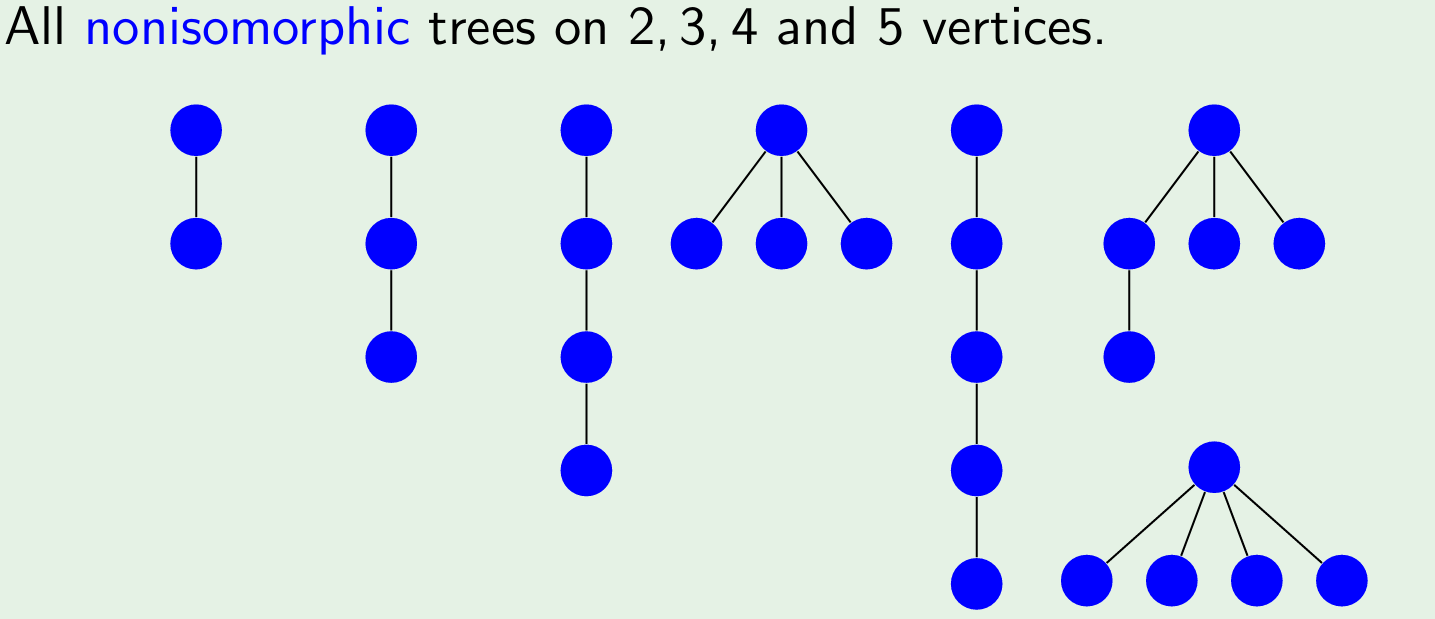
All nonisomorphic trees on 2,3,4 and 5 vertices.
Graph Traversals
Graph exploration
Often it is useful to “explore” a graph: visit vertices in some order and examine each one.
Search: Explore the graph until a particular vertex is discovered.
Traversal: Examine all the vertices of the graph
Two common graph exploration algorithms are Depth-first search/traversal (DFS) and Breadth-first search/traversal (BFS).
Both follow the same structure:
- Examine a vertex v
- Discover new vertices (i.e., neighbours of v)
- Move to the next discovered but not yet examined vertex
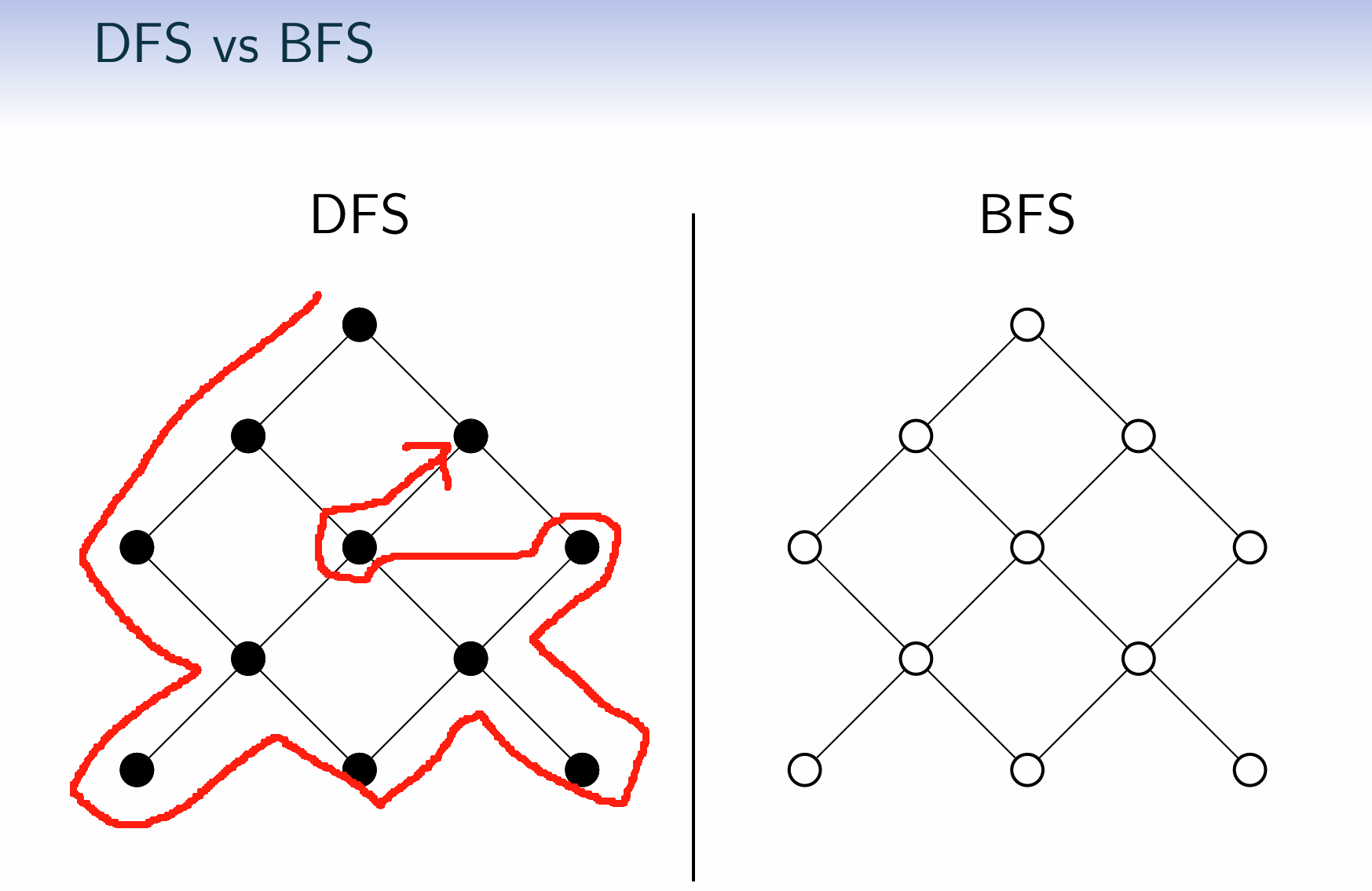
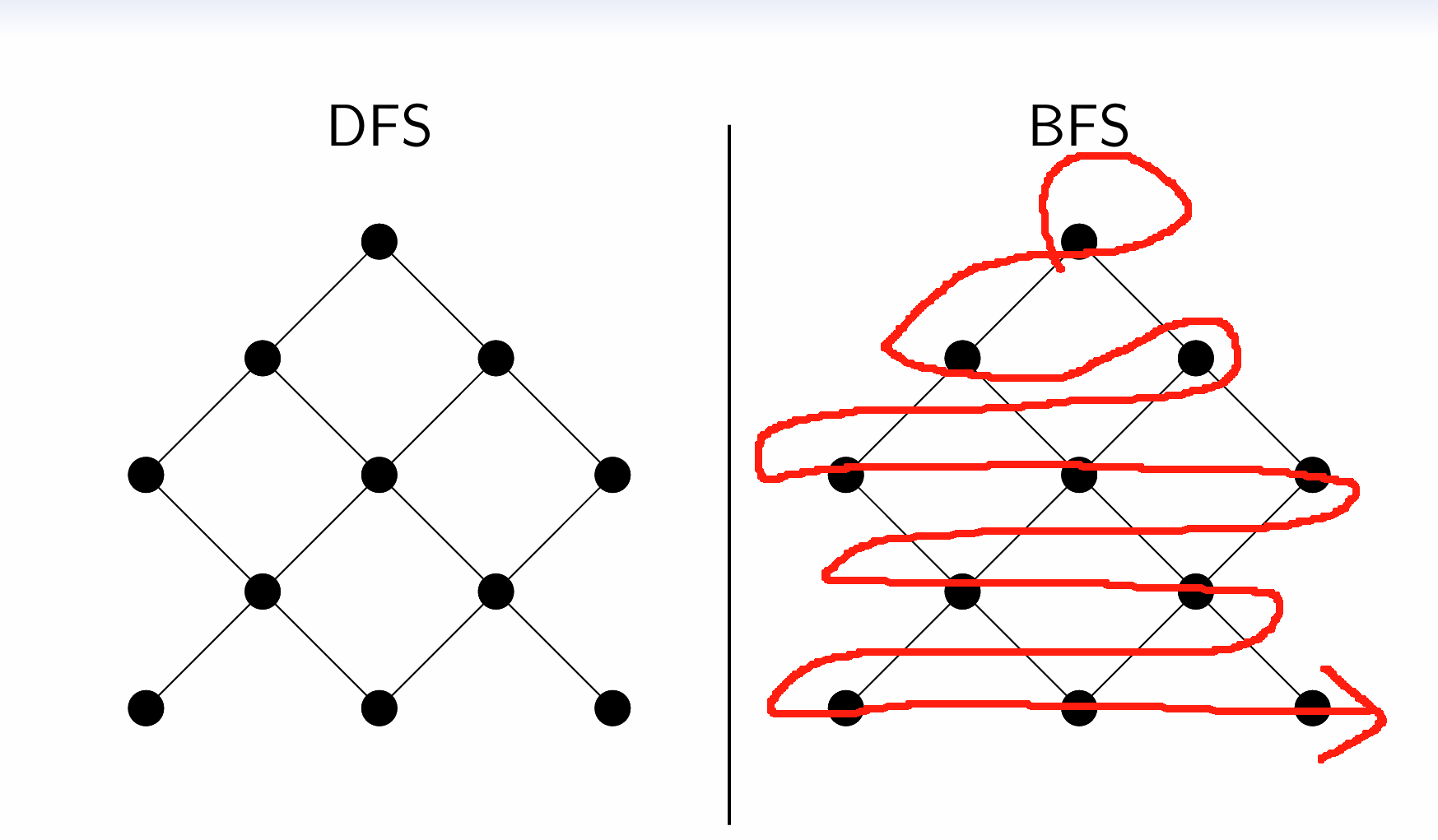
DFS: Examine vertices by most recently discovered
BFS: Examine vertices by least recently discovered
Special types of traversals
Often we are interested in traversals that have a certain property.
For example:
- Eulerian traversals: Visit all the edges exactly once
- Hamiltonian traversals: Visit all the vertices exactly once
欧拉-trail-所有边一次
汉密尔顿-path-所有点一次
Take Notice
In any given graph, these traversals may or may not exist.
Establishing the existence of such a traversal (decision problem) vs finding one if it exists (search problem) are subtly different problems.
Edge Traversal
Definition
For a graph G = (V,E).
Euler trail — trail containing every edge in E exactly once
Euler circuit — closed Euler trail
Characterisations
Suppose G is connected. Then G has an Euler circuit iff deg(v) is even for all $v ∈ V$.
Suppose G is connected. Then G has an Euler trail iff either it has an Euler circuit or it has exactly two vertices of odd degree.
Take Notice
- These characterisations apply to multigraphs as well
- For directed graphs the condition for existence of an Euler circuit is $indeg(v) = outdeg(v)$ for all $v ∈ V$
欧拉道路(Euler trail):所有边且每条边只走一次的路径,可以是开路径(起点和终点不同),也可以是闭路径(起点和终点相同)。
欧拉回路(Euler circuit):欧拉回路是欧拉道路的一种特殊情况,要求路径是闭合的,即起点和终点是同一个顶点。
Hence
exercise 1
Construct a graph with vertex set {0,1} ×{0,1}×{0,1} and with an edge between vertices if they differ in exactly two coordinates.
(a) How many components does this graph have?
(b) How many vertices of each degree?
(c) Euler circuit?
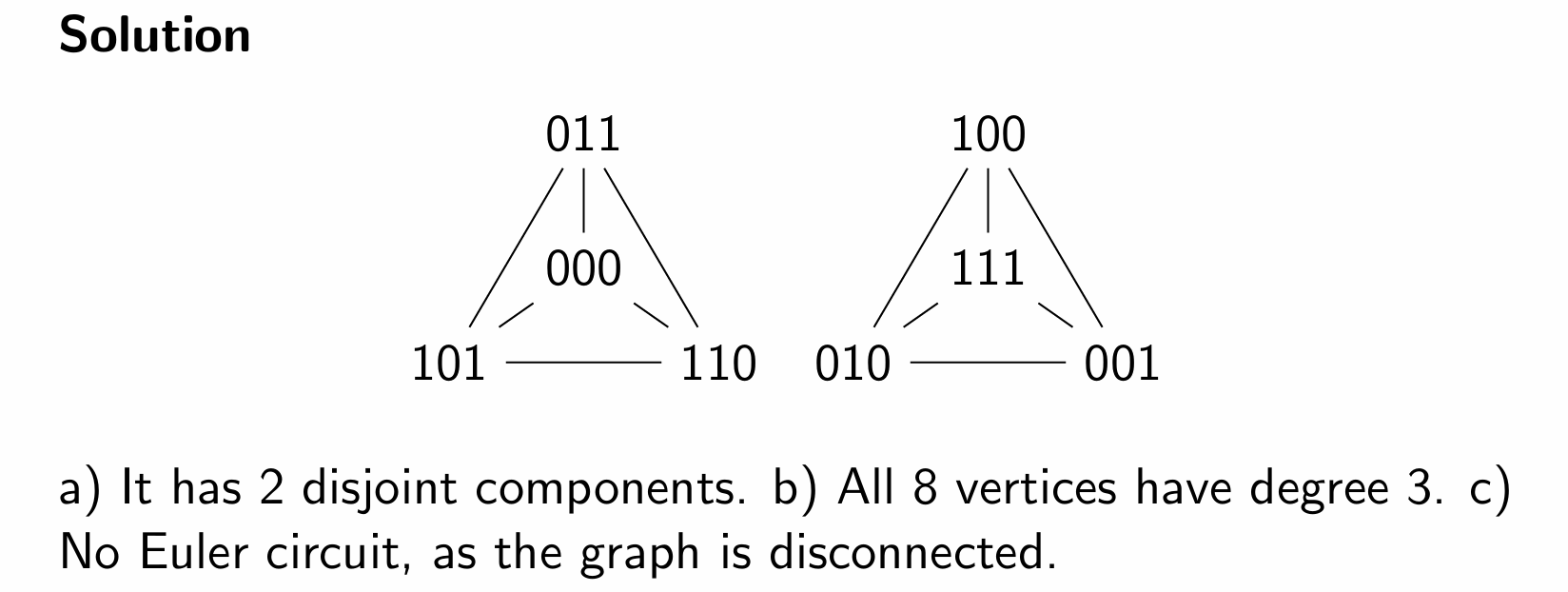
exercise 2
As the question above but with an edge between vertices if they differ in two or three coordinates.
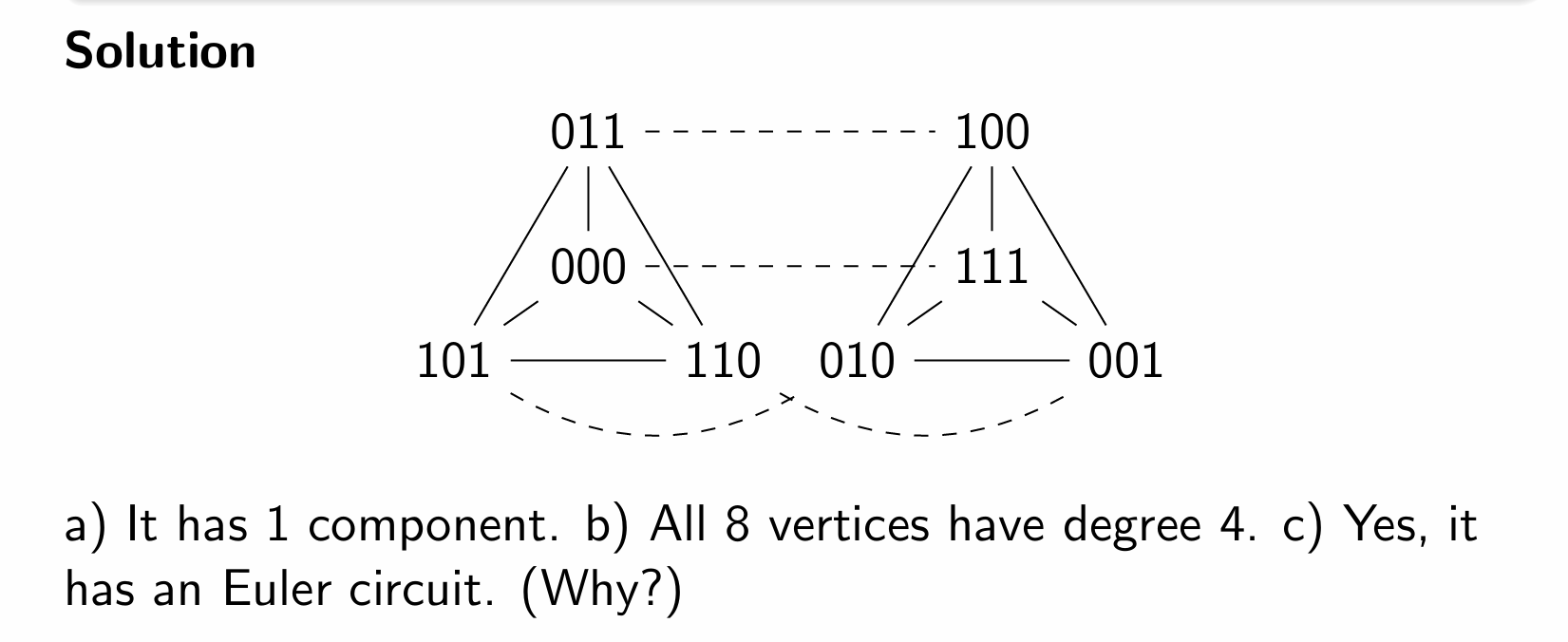
About why, we can see even degrees between each vertices.
exercise 3

因为在完全图中,n点有(n-1)个度,所以当n是奇数,他才有偶数个度。
完全二分图中,每个部分的点不和自己一个part的点连接,只和对面part的店连接,因此n和m都是偶数,度才是偶数。
三分图,设m,n,q三个部分。只有两两相加才能是偶数个度,因此要么全奇数,要么全偶数。
Vertex Traversal
Definition
- Hamiltonian path visits every vertex of graph exactly once
- Hamiltonian cycle visits every vertex exactly once except the last one, which duplicates the first
Take Notice
Finding such a cycle, or proving it does not exist, is a difficult problem — the worst case is NP-complete.
Examples (where the Hamiltonian cycle exists)
- Tetrahedron
- Hexahedron
- $K_m$ for all m
- $K_{m,n}$ iff m = n
Examples when a Hamiltonian cycle does not exist are much harder to construct.
Also, given such a graph, it is nontrivial to verify that there is no Hamiltonian cycle.
There is nothing obvious to specify that could assure us about this property. We have to check all possibilities.
In contrast, if a cycle is given, it is immediate to verify that it is a Hamiltonian cycle.
These situations demonstrate the often enormous discrepancy in difficulty of ‘proving’ versus (simply) ‘checking’.
Properties of Graphs
Colouring
Informally: assigning a “colour” to each vertex so that the vertices connected by an edge have different colours.
Formally: A mapping $c : V → [1..t]$ such that for every $e =(v,w) ∈ E$
The minimum t sufficient to effect such a mapping is called the chromatic number of a graph $G$ and is denoted $χ(G)$.
Take Notice
This notion is extremely important in operations research, esp. in scheduling.
There is a dual notion of ‘edge colouring’ — two edges that share a vertex need to have different colours. Curiously enough, it is much less useful in practice.
Properties of the Chromatic Number
- $χ(K_n) = n$
- If G has n vertices and $χ(G) = n$ then $G = K_n$
- If $χ(G)$ = 1 then G is totally disconnected: it has 0 edges.
- If $χ(G) = 2$ then G is bipartite
- For any tree $χ(T) = 2$
- For any cycle $C_n$ its chromatic number depends on the parity of n — for n even $χ(C_n) = 2$, while for n odd $χ(C_n) = 3$.


Cliques
Graph $G′ = (V′,E′)$ is a subgraph of $G = (V,E)$, if $V′ ⊆ V$ and $E′ ⊆ E$.
Definition
A clique in G is a complete subgraph of G. A clique of k nodes is called k-clique.
The size of the largest clique is called the clique number of the graph and denoted $κ(G)$.
- 团是完全图
- 团数 是子图的最大团的定点数。
Theorem
Proof
Every vertex of a clique requires a different colour, hence there must be at least $κ(G)$ colours.
However, this is the only restriction. For any given k there are graphs with $κ(G) = k$, while $χ(G)$ can be arbitrarily large.
Take Notice
This fact (and such graphs) are important in the analysis of parallel computation algorithms.
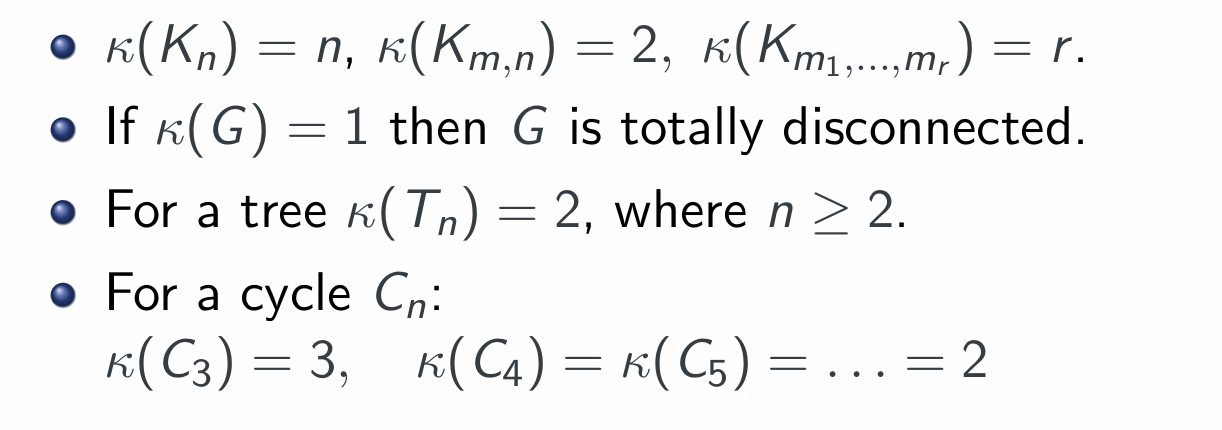
exercise 1
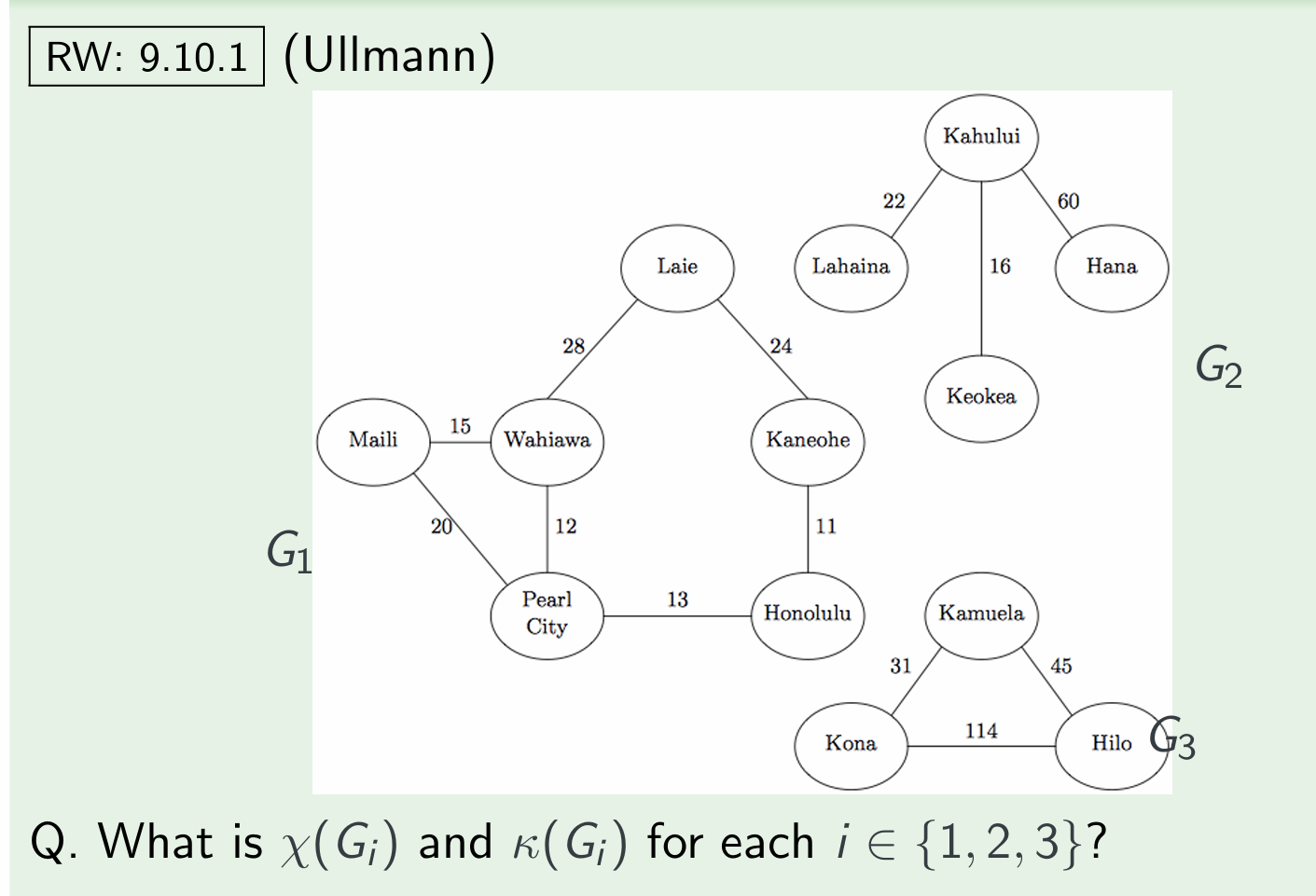
A. $χ(G1) = κ(G1) = 3$; $χ(G2) = κ(G2) = 2$; $χ(G3) = κ(G3) = 3$
exercise 2

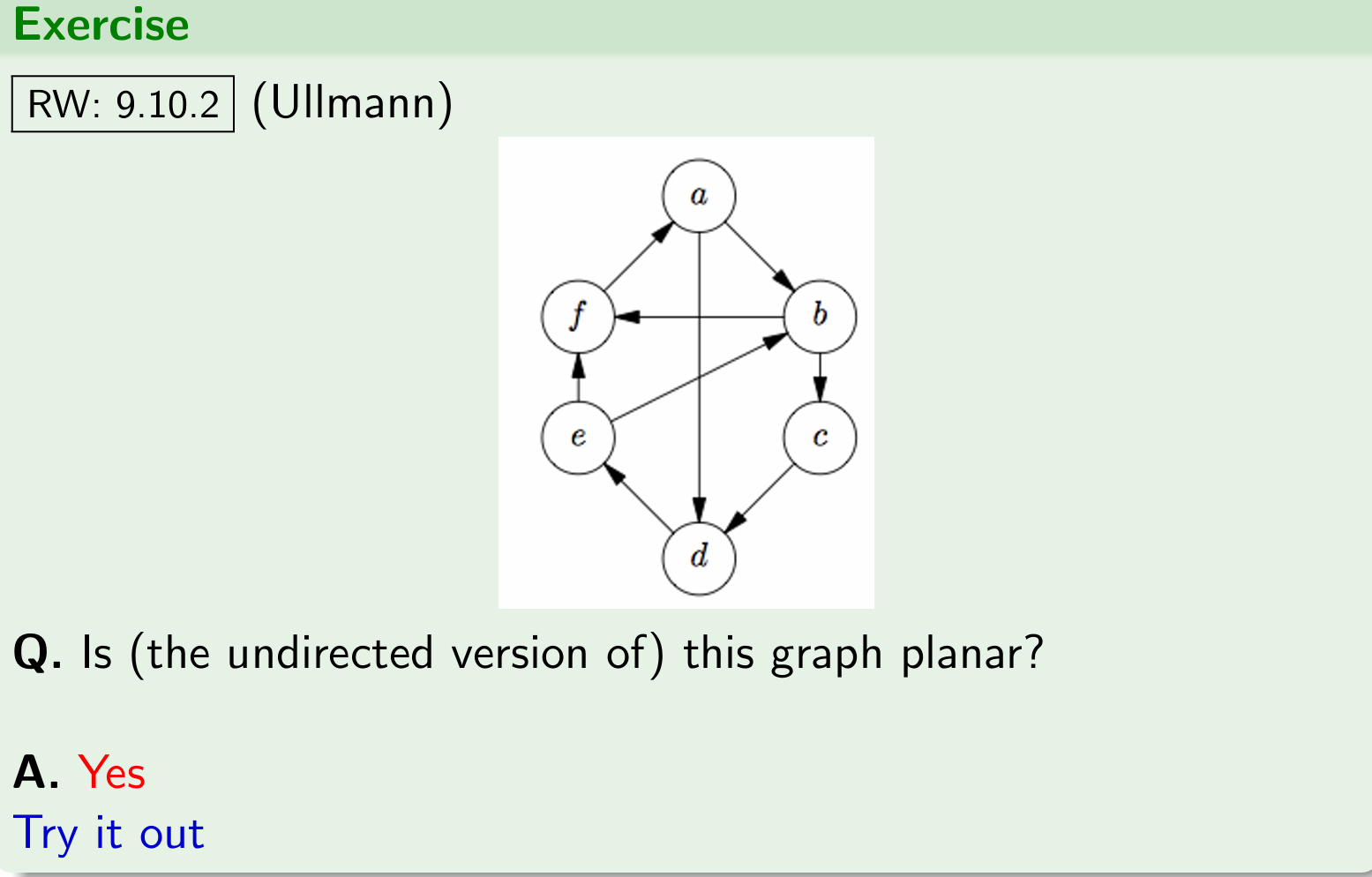
Timetable scheduling
Planar Graphs
Definition
A graph is planar if it can be embedded in a plane without its edges intersecting.
Theorem
If the graph is planar it can be embedded (without self-intersections) in a plane so that all its edges are straight lines.
Take Notice
This notion and its related algorithms are extremely important to VLSI (very large-scale integration– refers to an IC or technology with many devices on one chip) and visualizing data.
是说嵌入平面,线不会交叉。不要把planar理解成二维三维差别。
Nonplanar graphs
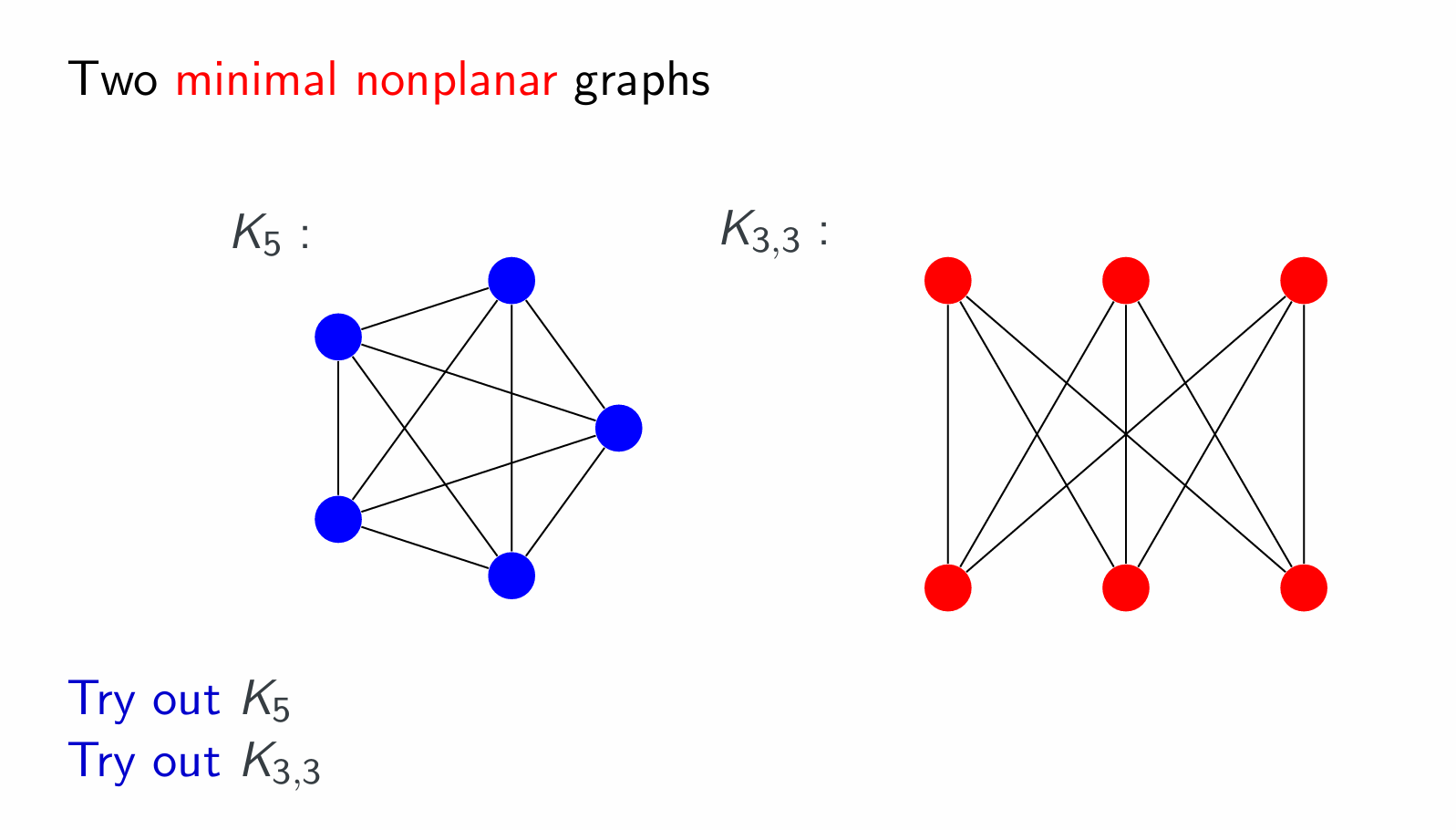
They are not planar graphs.
Three utilities problem

Testing for nonplanarity
Theorem
If graph G contains, as a subgraph, a nonplanar graph, then G itself is nonplanar.
For a graph, edge subdivision means to introduce some new vertices, all of degree 2, by placing them on existing edges.
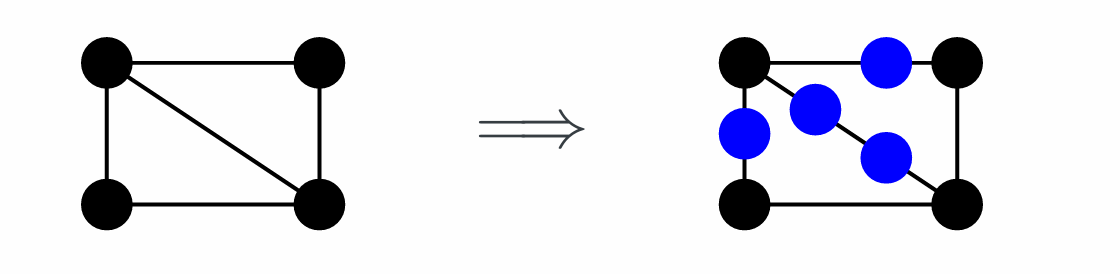
We call such a derived graph a subdivision of the original one.
Theorem
If a graph is nonplanar then it must contain a subdivision of $K5$ or $K{3,3}$.
More nonplanar graphs
Theorem
$K_n$ for $n ≥ 5$ is nonplanar.
Proof
It contains $K_5$: choose any five vertices in $K_n$ and consider the subgraph they define.
Theorem
$K_{m,n}$ is nonplanar when $m ≥ 3$ and $n ≥ 3$.
Proof
They contain $K_{3,3}$ — choose any three vertices in each of two vertex parts and consider the subgraph they define.
exercise 1

Welcome to point out the mistakes and faults!