Extracted from the raw material from UNSW COMP9101, thanks for Serge Gaspers.
- Lec
- Why should you study algorithms?
- Algorithm analysis: why is correctness important?
- Algorithm analysis: why is efficiency important?
- Why is algorithm design important?
- Code-first approach
- Separating design from implementation
- Course Learning Outcomes
- What is an algorithm?
- Scope
- Problem structure
- Example problem: Geese in a Trenchcoat
- puzzle
- Lec2
- proof
- mergesort
- Stable Matching Problem
- puzzle
Lec
Why should you study algorithms?
This course is about problem solving and communication.
Two pillars
1. algorithm design
algorithm design is the task of designing a process which, when executed, solves a particular problem;
This process might be a way of calculating something, selecting something, etc.
2. algorithm analysis
algorithm analys is is the task of assessing such a process (either your own work or someone else’s) with regards to the problem.
Does it always give the intended result?
How quickly does it run?
Algorithm analysis: why is correctness important?
A program which fails a test case is wrong, but a program which passes a test case isn’t necessarily correct.
Failure on an obscure case can be catastrophic!
Testing is good, good testing is better, proof is best.
What makes a strong test?
How do you prove (or at least justify in general terms) correctness and explain it to a peer?
Algorithm analysis: why is efficiency important?
Using better hardware might save a small (or even large) percentage of the running time of a program.
However a more efficient algorithm can make staggering improvements!
Sorting one million numbers could take an hour using bubble sort, or a second using merge sort.
For more sophisticated algorithms, details such as the choice of data structures are also important.
Why is algorithm design important?
Algorithm design is the ‘planning stage’, where we decide what our program should do.
We have all tried to code programs only to find a fundamental flaw in our approach later on.
A systematic approach to algorithm design separates engineers from “code monkeys”.
Code-first approach
Solving the problem as you code can lead you into a “debugging vortex”, applying patches without fixing the underlying issue, or to accept incorrect code that passes weak tests.
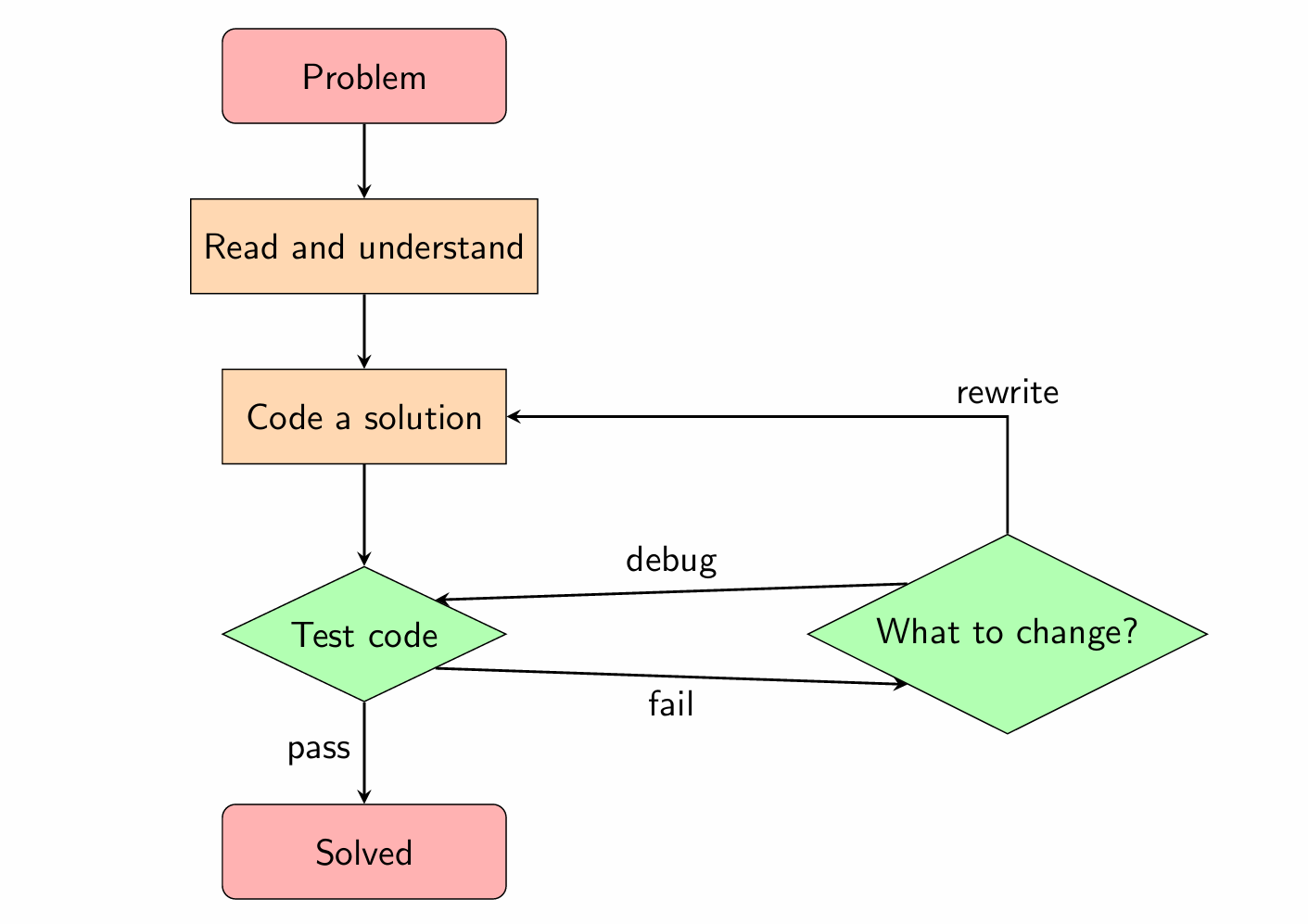
Separating design from implementation allows high-level reasoning to confirm that the algorithm meets the requirements of the problem before making implementation decisions.
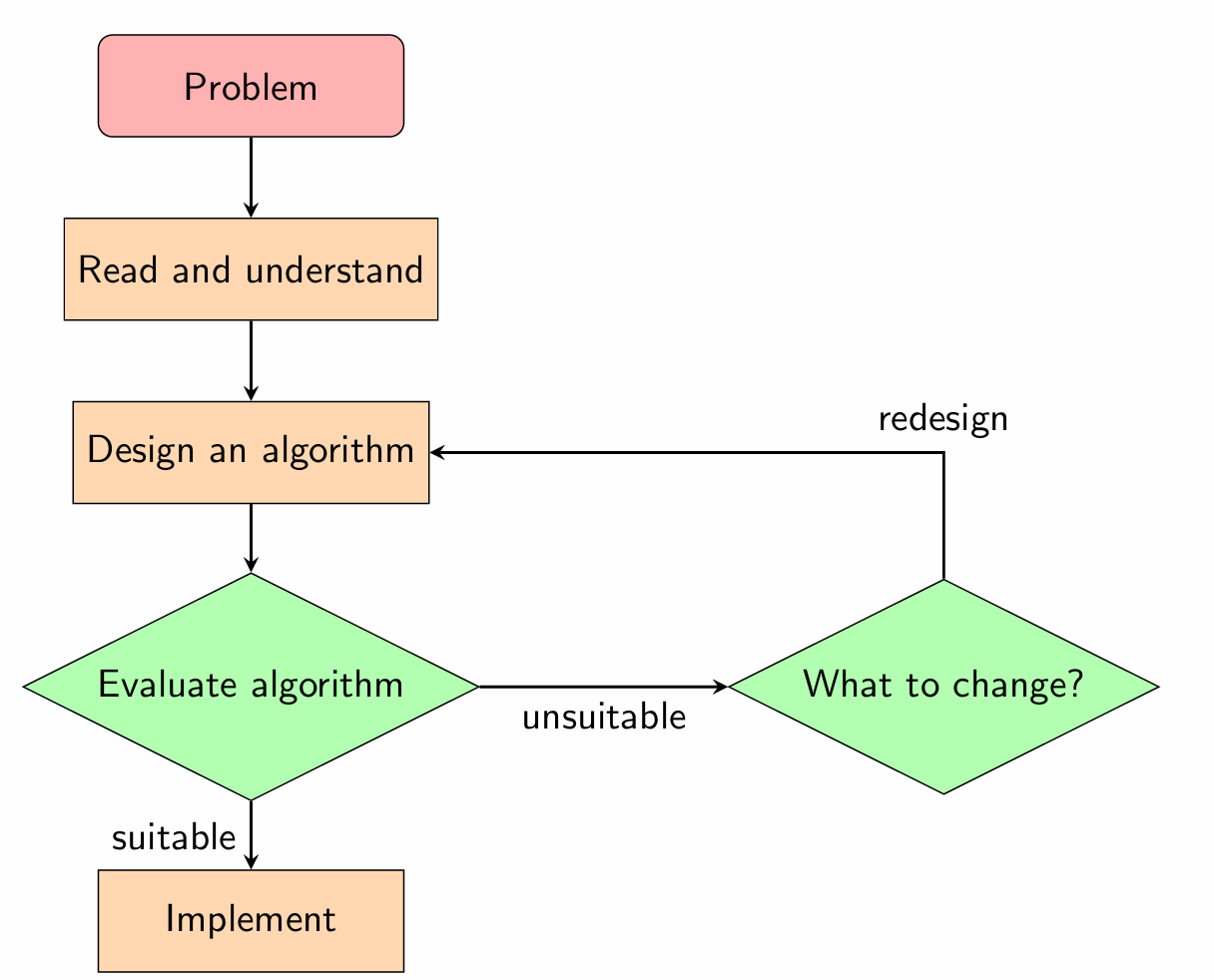
Separating design from implementation
We will talk about algorithms in plain English. We will avoid pseudocode, and we will especially avoid using code in any programming language.
Implementation is outside the scope of this course.
We’ll focus on the big picture, to prepare you to:
work in teams on large projects
communicate clearly and persuasively with stakeholders including colleagues, clients and the public
compile design briefs and documentation,
which are all important skills for the modern computing professional.
Course Learning Outcomes
Explain how standard design techniques are used to develop algorithms.
Solve problems by creatively applying algorithm design techniques.
Communicate algorithmic ideas at different abstraction levels.
Evaluate the efficiency of algorithms and justify their correctness.
Apply the LATEX typesetting system to produce high-quality technical documents.
What is an algorithm?
An algorithm is a collection of precisely defined steps that can be executed mechanically, i.e. without intelligent decision-making.
Designing a recipe involves creativity, executing it does not; the same is true of algorithms.
The word “algorithm” comes by corruption of the name of Muhammad ibn Musa al-Khwarizmi, a Persian scientist 780–850, who wrote an important book on algebra, “Al-kitab al-mukhtasar fi hisab al-gabr wa’l-muqabala”.
Scope
In this course we will deal only with algorithms that are:
sequential: comprised by a sequence of steps, which can only be executed one at a time, and
deterministic: each step always gives the same result for the same input.
Parallel algorithms and randomised algorithms are interesting and powerful, but beyond the scope of this course.
Problem structure
Problems may have ‘flavour text’: a brief story for context. Abstracting this information away is a key first step.
Algorithm design tasks may also include an input and output specification if it is not otherwise clear.
In this course, we are usually not concerned with the format in which this information is presented, nor with the minute details of how an implementation of the algorithm accesses input or produces output.
However it is crucially important that our algorithm always transforms valid input into the appropriate output efficiently.
We’ll usually measure the efficiency of algorithms using asymptotic analysis, rather than the exact time or number of operations taken.
You will have already encountered big-Oh notation.
For example, a process consisting of two nested loops “for each i from 1 to n, for each j from 1 to n” takes $O(n^2)$ time.
We’ll formalise these ideas in the next lecture.
We’ll usually use the unit-cost model of computation, where each machine operation (+, −, ×, ÷ and accessing memory) takes constant time.
- The only exception is when we discuss algorithms to multiply large integers in Module 2: there we’ll use the logarithmic-cost model, where these operations take time dependent on the width (number of bits) of the input numbers.
Example problem: Geese in a Trenchcoat

Problem
There are n geese in a gaggle, of heights $h_1,…,h_n$. Each $h_i$ is a positive integer.
They need to select two of themtoweara trenchcoat together,with one standing on top of the other.The trenchcoat will only fit if the two geese have total height exactly equal to H.
Design an algorithm which runs in $O(n logn)$ time and determines whether the there two geese who can wear the trenchcoat together.
Abstraction
Design an algorithm which runs in $O(n logn)$ time and, given an array $A$ consisting of $n$ positive integers and a positive integer $X$, determines whether there are two indices $i<j$ such that $A[i]+A[j]=X$.
- If we fix index i (one of thegeese), then we know that a matching element must contribute the rest of the total (make up the rest of the required height).
- Let’s try all values of i.
Example problem: Geese in a Trenchcoat
Attempt 1
For each goose i,check whether a matching goose (whose height is $H−h_i$) exists, and answer yes if one is found.
This is not an algorithm!
It does not describe how to actually perform this check.
Why does this matter?
- For a small number of geese,a human could follow this process, checking by eye. If there were say one million geese, it’s not at all clear how to do the check.
- Perhaps this check takes time?
The Big-Oh is:
Attempt 2
For each goose i, a matching goose must have height $H - h_i$. For each other goose $j$, check whether $h_j$ equals this quantity, and answer yes if one is found.
- This is actually an algorithm
- It is also a correct algorithm.
- Does it correctly answer all ‘yes’ instances?
- Does it correctly answer all ‘no’ instances?
Unfortunately it’s too slow: “for each i (of which there are n), for each j (of which there are n), do something” is already $n^2$ iterations.
- Can we search efficiently for the correct j, rather than trying them all? Perhaps if the heights are well organised.
Algorithm
Sort the geese in ascending order of height, using merge sort.
For each goose i, a matching goose must have height $H - h_i$. Since the heights are now nondecreasing, we can search for this required length using binary search, and answer yes if it is found.
Is this algorithm correct?
- Does it correctly answer all ‘yes’ instances?
- Does it correctly answer all ‘no’ instances?
What is the time complexity of this algorithm?
- How long does the sort take?
- How many times is the binary search run?
- How long does each binary search take?
You will usually have to justify that your algorithm is correct and that it runs with in the specified time complexity.
puzzle
Problem: Tom and his wife Mary went to a party where nine more couples were present.
Not everyone knew everyone else, so people who did not know each other introduced themselves and shook hands. People who knew each other from before did not shake hands.
Later that evening Tom got bored, so he walked around and asked all other guests (including his wife) how many hands they had shaken that evening, and got 19 different answers.
How many hands did Mary shake?
How many hands did Tom shake?
Lec2
Heap sort is faster than bubble sort.
Linear search is slower than binary search.
The statements on the previous slide are most commonly made in comparing the worst case performance of these algorithms.
They are actually false in the best case!
In most problems in this course, we are concerned with worst case performance, so as to be robust to maliciously created (or simply unlucky) instance
We will hardly ever discuss the best case.
Question
If $f(100) > g(100)$, then does f represent a greater running time, i.e. as lower algorithm?
Answer
Not necessarily! $n=100$ might be an outlier, or too small to appreciate the efficiencies of algorithm $f$. We care more about which algorithm scales better.
Big-Ohnotation: Examples
Example 1
Let $f(n)=100n$. Then $f(n)=O(n)$, because $f(n)$ is at most 100 times $n$ for largen.
Example 2
Let $f(n)=2n+7$. Then $f(n)=O(n^2)$, because $f(n)$ is at most 1 times $n^2$ for large $n$. Note that $f(n)=O(n)$ is also true in this case.
这里注意啊,区别下COMP9101和COMP9020的区别,不太一样,算法没数学那么严谨看来。 $f(n)=2n+7$. Then $f(n)=O(n^2)$ $f(n)=O(n)$ is also true, 只要是上界函数,甭管n还是n方还是n立方,只要渐近增长大就是上界。
Example 3
Let $f(n)=0.001n^3$. Then $f(n) \neq O(n^2)$, because for any constant multiple of $n^2$, $f(n)$ will eventually exceed it.
inserting into a binary search tree takes $O(h)$ time in the worst case, where h is the height of the tree, and
insertion sort runs in $O(n^2)$ time in the worst case, but $O(n)$ in the best case.
Question
The definition states that we only care about the function values for “large enough” n. How large is “large enough”? Put differently, how small is “small enough” that it can be safely ignored in assessing whether the definition is satisfied?
Answer
Everything is small compared to the infinity of n-values beyond itself.
It doesn’t matter how $f(1)$ compares to $g(1)$, or even how $f(1,000,000)$ compares to $g(1,000,000)$. We only care that $f(n)$ is bounded above by a multiple of $g(n)$ eventually.
Big-Omega notation
Definition
We say $f(n)=Ω(g(n))$ if for large enoughn, $f(n)$ is at least a constant multiple of $g(n)$.
Big-Theta notation
Definition
We say $f(n)=Θ(g(n))$ if
$f(n)$ and $g(n)$ are said to have the same asymptotic growth rate.
$f(n)$ and $g(n)$ are said to have the same asymptotic growth rate.
Analgorithm whose running time is $f(n)$ scales as well as one whose running time is $g(n)$.
It’s true-ish to say that the former algorithm is ‘as fast as’ the latter.
Question
You’ve previously seen statements such as
bubble sort runs in $O(n^2)$ time in the worst case.
Should these statements be written using $Θ(·)$ instead of $O(·)$?
Answer
They can, but they don’t have to be. The statements
bubble sort runs in $O(n^2)$ time in the worst case
and
bubble sort runs in $Θ(n^2)$ time in the worst case
are both true: they claim that the worst case running time is at most quadratic and exactly quadratic respectively.
The $Θ(·)$ statement conveys more information than the $O(·)$ statement. However in most situations we just want to be sure that the running time hasn’t been underestimated, so $O(·)$ is the important part.
Note that sometimes confusions arise because people write the more commonly used $O(·)$ as a shorthand for the less commonly used $Θ(·)$! Please be aware of the difference.
Sum property
Fact of sum
If $f_1 = O(g_1)$ and $f_2 = O(g_2)$, then $f_1 +f_2 = O(g_1 +g_2)$.
The last term $O(g_1 +g_2)$ is often rewritten as $O(max(g_1,g_2))$, since $g_1 + g_2 ≤ 2 max(g_1,g_2)$.
The same property applies if $O$ is replaced by $Ω$ or $Θ$.
Fact of Product
If $f_1 = O(g_1)$ and $f_2 = O(g_2)$, then $f_1 ·f_2 = O(g_1 ·g_2)$.
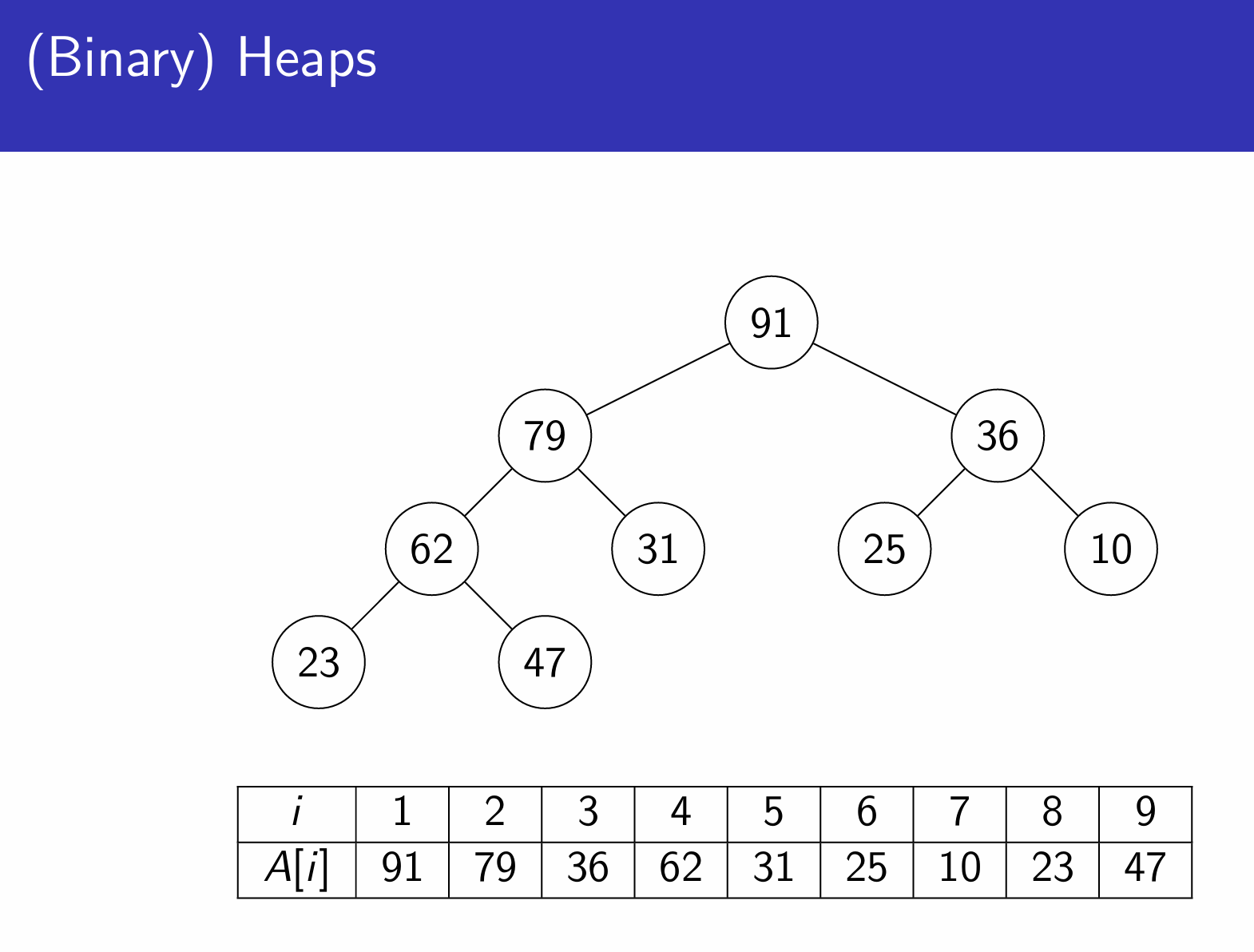
(Binary)Heaps
Store items in a complete binary tree, with every parent comparing $≥$ all its children.
This is a max heap; replace $≥$ with $≤$ for min heap.
Used to implement priority queue.
Operations
Build heap: $O(n)$
Find maximum: $O(1)$
Delete maximum: $O(log n)$
Insert: $O(log n)$
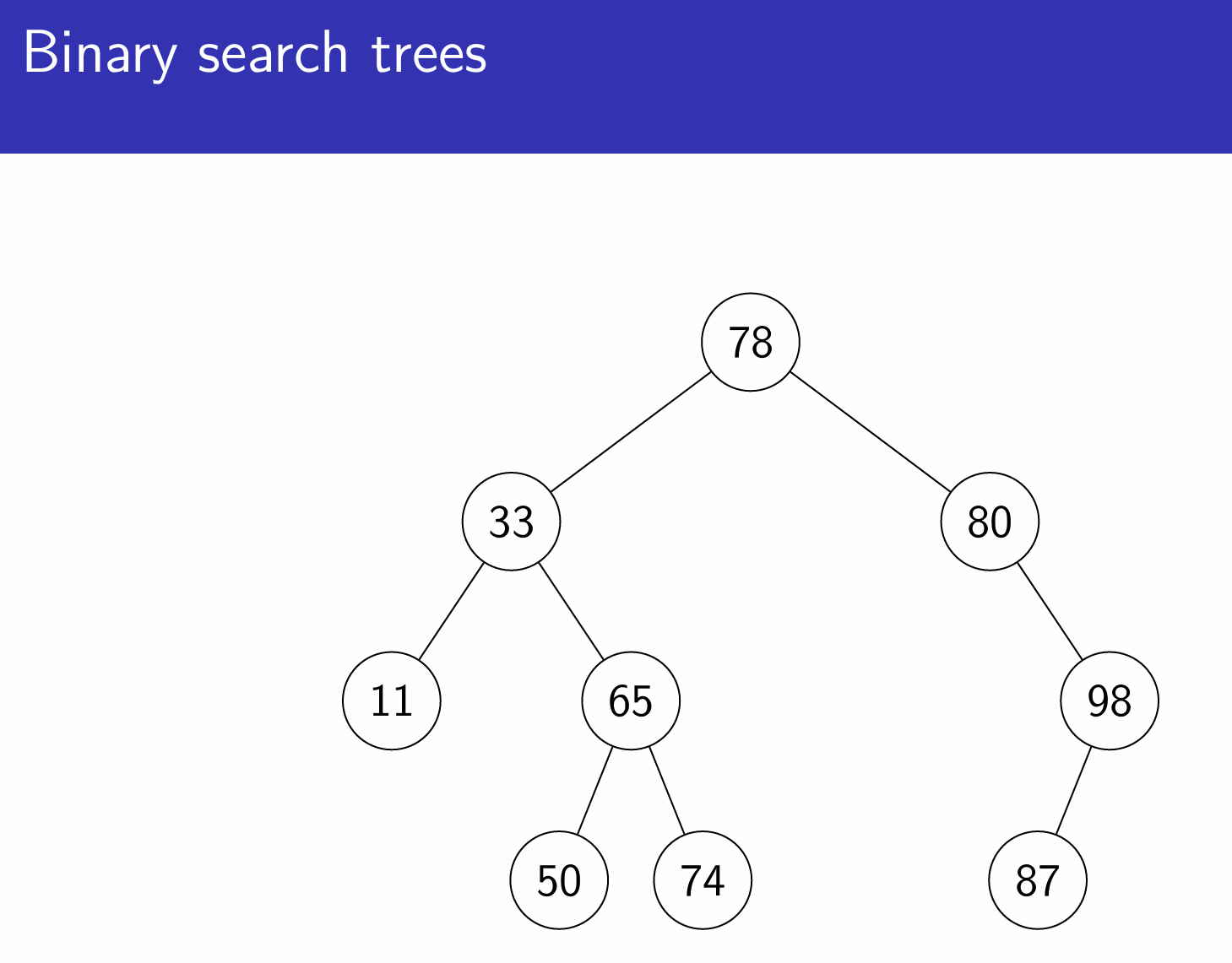
Binary search trees
Store (comparable) keys or key-value pairs in a binary tree, where each node has at most two children, designated as left and right
Each node’s key compares greater than all keys in its left subtree, and less than all keys in its right subtree.
Operations
Let h be the height of the tree, that is, the length of the longest path from the root to the leaf.
Search: $O(h)$
Insert/delete: $O(h)$
Self-balancing binary search trees
In the best case, $h ≈ log_2 n$. Such trees are said to be balanced.
In the worst case, $h ≈ n$, e.g. if keys were inserted in increasing order.
Fortunately, there are several ways to make a self-balancing binary search tree (e.g. B-tree, AVL tree, red-black tree).
Each of these performs rotations to maintain certain invariants, in order to guarantee that $h = O(log n)$ and therefore all tree operations run in $O(log n)$ time.
Red-black trees are detailed in CLRS, but in this course it is sufficient to write “self-balancing binary search tree” without specifying any particular scheme.
Frequency tables
名字其实就是“频率统计”的意思,像是字典。
Problem
You are given an array A of $n-1$ elements. Each number from 1 to n appears exactly once, except for one number which is missing.
Find the missing number.
Idea
Record whether you’ve seen each possible value.
This leads to a linear time, linear space algorithm.
这个Idea是频率统计的方法步骤,但是空间复杂度比较高 $O(n)$,以下是控制空间复杂度为 $O(1)$ 的方法
Challenge
How could you solve the problem in linear time and constant space?
steps
To count the occurrences of integers from 1 to m, simply make a zero-initialised array of frequencies and increment every time the value is encountered.
The real question is how to count the occurences of other kinds of items, such as large integers, strings, and so on.
Try to do the same thing: map these items to integers from 1 to m, and count the occurences of the mapped values.
方法1:求和

方法2:XOR


假设 A = [1, 2, 4, 5],我们要找缺失的数 3,n = 5。
1 ⊕ 2 ⊕ 3 ⊕ 4 ⊕ 5
= (1 ⊕ 2) ⊕ 3 ⊕ (4 ⊕ 5)
= 3 ⊕ 3 ⊕ 9
= 0 ⊕ 9
= 9
Then
1 ⊕ 2 ⊕ 4 ⊕ 5
= (1 ⊕ 2) ⊕ (4 ⊕ 5)
= 3 ⊕ 9
= 10
完整的 XOR ⊕ A 里的 XOR = 9 ⊕ 10 = 3
Hash tables
Store values indexed by keys.
Hash function maps keys to indices in a fixed size table.
Ideall no two keys map to the same index.
Operations(expected)
Search for the value associated to a given key: $O(1)$
Update the value associated to a given key: $O(1)$
Insert/delete: $O(1)$
A situation where two (or more) keys have the same hash value is called a collision.
When mapping from a large key space to a small table, it’s impossible to completely avoid collisions.
There are several ways to manage collisions - for example, separate chaining stores a linked list of all colliding key-value pairs at each index of the hash table.
Operations (worst case)
Search for the value associated to a given key: $O(n)$
Update the value associated to a given key: $O(n)$
Insert/delete: $O(n)$
proof
Propositional logic
Propositions are true/false statements. Some examples:
The sky is orange.
Basser Steps consists of more than 100 stairs.
Everyone in this room is awake.
The goal of an argument is usually to establish a relationship between propositions, often also using the following operations.
| Notation | Meaning | Formal term |
|---|---|---|
| ¬P | not P | negation |
| P∧Q | P and Q | conjunction |
| P∨Q | P(inclusive-) or Q | disjunction |
| P→Q | if P then Q | implication |
The quantifiers “for all” ($∀$) and “for some” ($∃$) are also very common.
mergesort
The depth of recursion in mergesort is $log_2 n$
On each level of recursion, merging all the intermediate arrays takes $O(n)$ steps in total.
Thus, mergesort always terminates, and in fact it terminates in $O(n log_2 n)$ steps.
Stable Matching Problem
Suppose you have hired n frontend engineers and n backend engineers to build n apps in pairs.
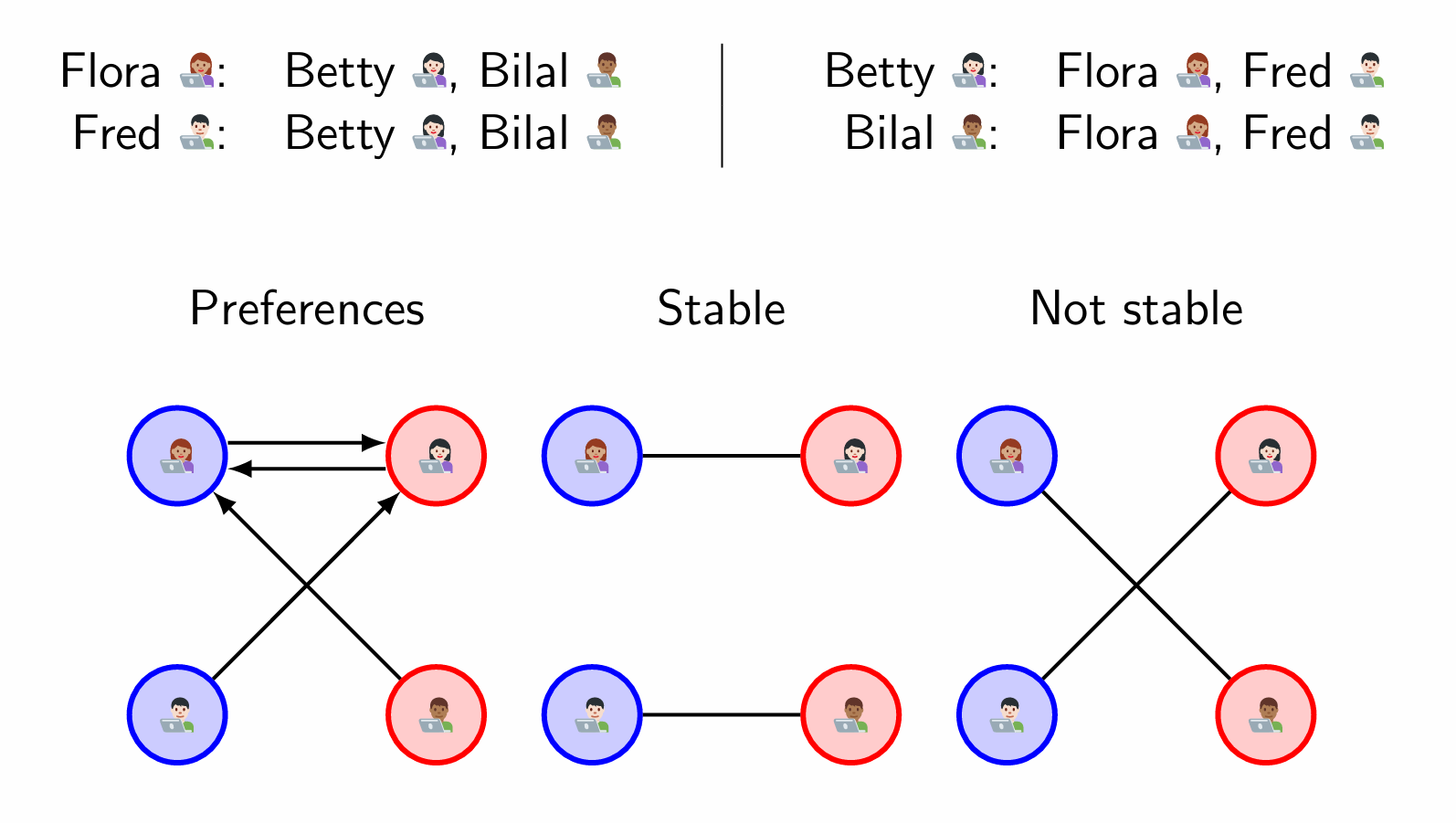
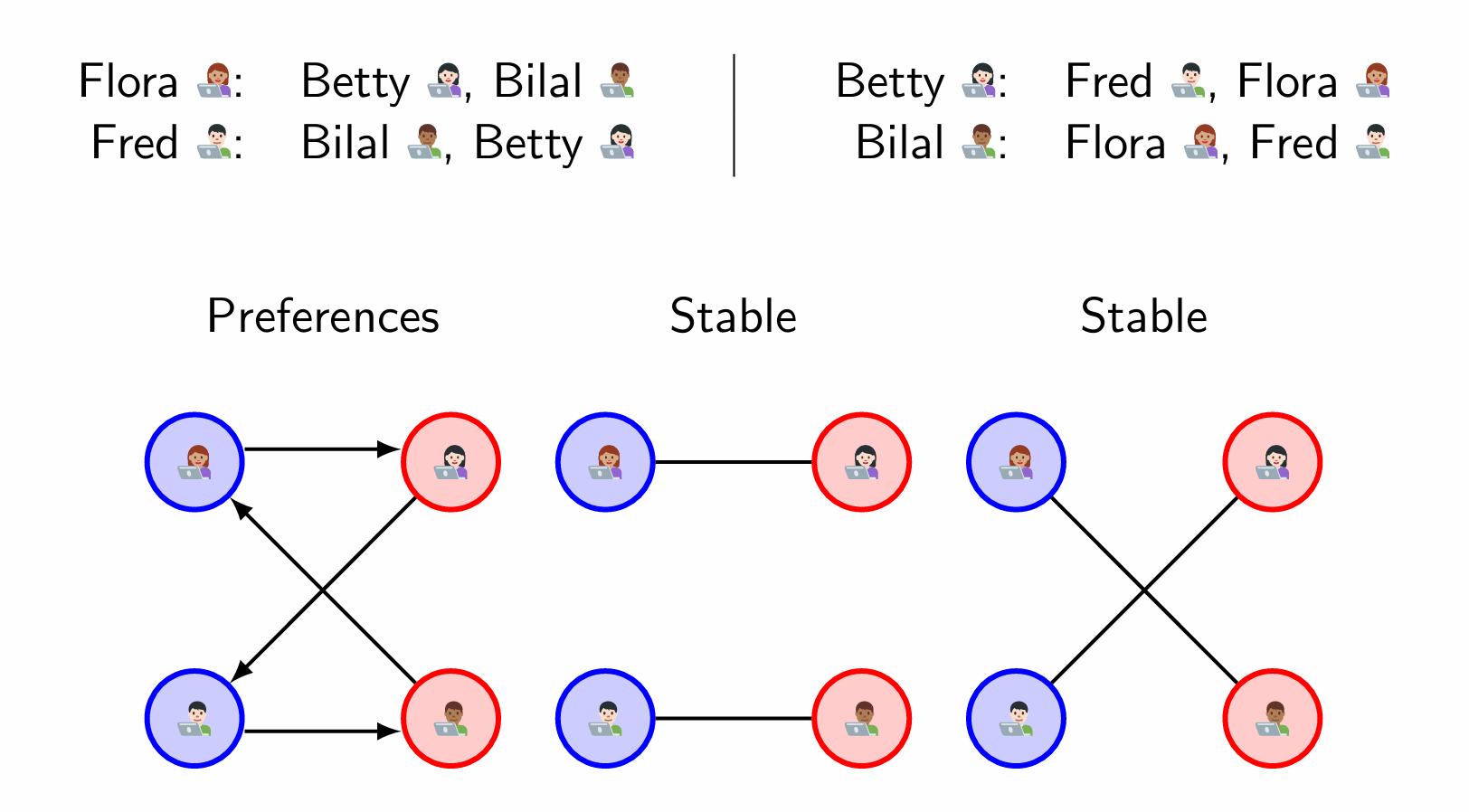
Question
Give n frontend and n backend engineers, how many ways are there to match them, without regard for preferences?
Answer
$n!≈(n/e)^n$ - more than exponentially many in $n$ ($e≈2.718$).
这个为啥不是 n 乘 n, 和之前数学学统计概率那儿不一样。因为数学里我遇到的问题是,第一个篮子5苹果,第二个篮子3苹果,几种选择方法?是$5 \times 3 = 15$种挑法。这里说的是匹配问题,人人都要匹配,因此是$n! = n \times (n-1) \times (n-2) \dots \times 1$.
$n!≈(\frac{n}{e})^n$ 是 斯特林近似 (Stirling’s approximation) 的一种简化形式,它用于近似计算 阶乘 $𝑛!$ 的增长速度。
阶乘的增长速度比指数增长更快,但比超指数增长(如 $n^n$ )慢。
Question
Is it true that for every possible collection of n lists of preferences provided by all frontend engineers, and n lists of preferences provided by all backend engineers, a stable matching always exists?
Answer
Perhaps surprisingly, yes!
Gale-Shapley algorithm
Question
Can we find a stable matching in a reasonable amount of time?
Answer
Yes, using the Gale-Shapley algorithm.
Produces pairs in stages, with possible revisions.
Frontend engineers will be pitching to backend engineers (arbitrarily chosen). Backend engineers will decide to accept a pitch or not.
A frontend engineer who is not currently in a pair will be
called solo.
Start with all frontend engineers solo.
Outline of algorithm
While there is a solo frontend engineer who has not pitched to all backend engineers, pick any such solo frontend engineer, say Femi.
Femi pitches to the highest ranking backend engineer Brad on his list, ignoring any who he has pitched to before.
If Brad is not yet paired, he accepts Femi’s pitch (at least tentatively).
Otherwise, if Brad is already paired with someone else, say Frida
- if Brad prefers Femi to Frida, he turns down Frida and makes a new pair with Femi (making Frida now solo) 50
- otherwise, Brad will turn down Femi and stay with Frida.
Question. Does the algorithm work? And is it efficient?
To answer this, we will prove the following 3 claims:
Claim1
The algorithm terminates after $≤ n^2$ rounds.
Claim2
The algorithm produces a perfect matching, i.e.when the algorithm terminates, the $2n$ engineers form $n$ separate pairs.
Claim3
The matching produced by the algorithm is stable.
注意,把上文的前端后端组我称呼为A, B 组,其实也对应视频里的MALES和FEMALES两个组。
A组是从偏好的高到低选,B组是从偏好的低到高选。
A组优先选人,一轮选完(不求全部配对),因为有可能后者被前者抢了第一偏好,因此在第二轮、第三轮等再匹配。

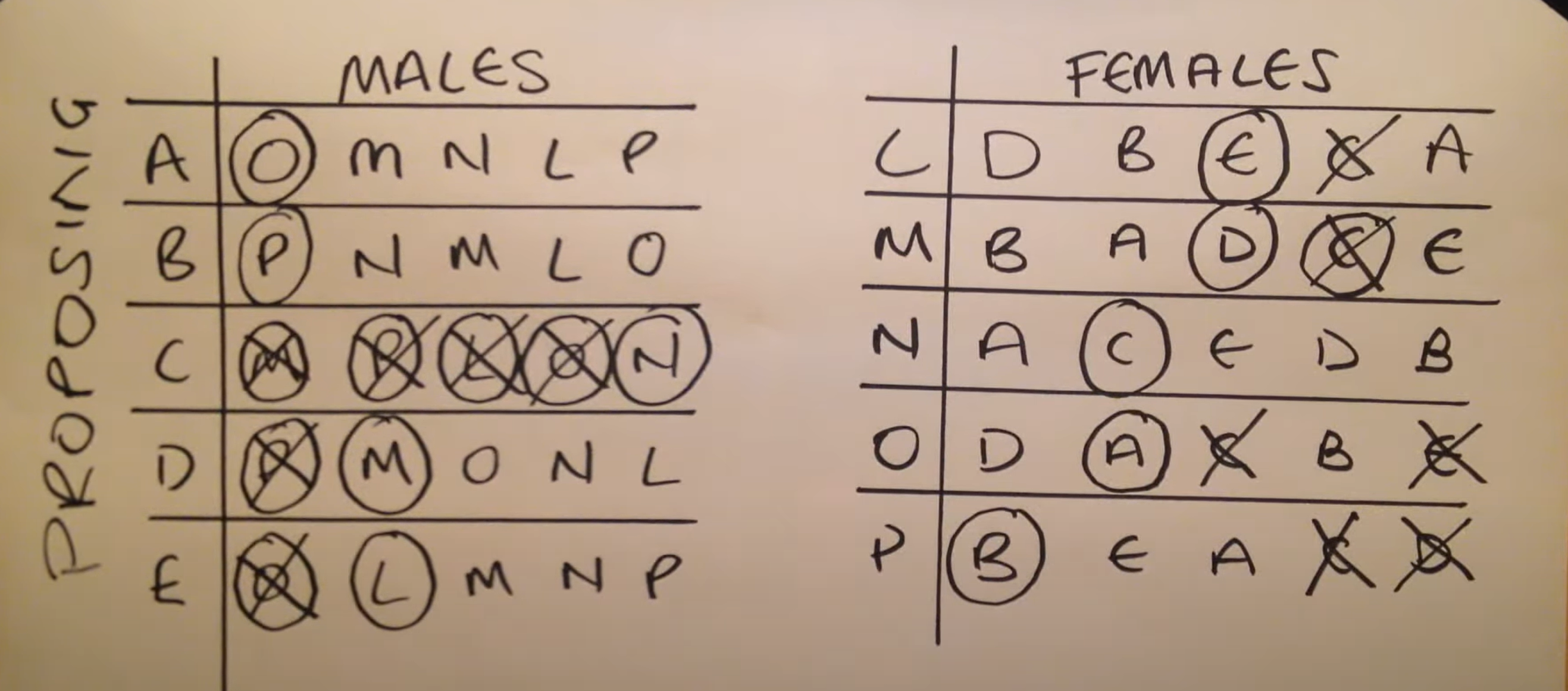
关于此算法更有利于追求方,被追求方少利
That’s right, the algorithm is always unfair for one party because it is not symmetric. It is designed to give the “proposing party” the best possible stable match, and the “accepting party” potentially a worse, but still stable match.
But the goal of the algorithm is to generate a stable match, and that’s what it does.
In fact, one can prove that the Gale-Shapley algorithm is optimal for the party proposing and pessimal (i.e. least favourable) for the party rejecting. This is actually a key fact about the algorithm that allows us to find when there is a unique stable matching!
They mean that a backend engineer will only switch their pairing if they are presented with a frontend engineer that they prefer more. The sequence of frontend engineers that a particular backend engineer is pair is non-decreasing in preference over time and will eventually become constant.
Say a backend engineer is first offered with their 6th preference, then they accept by default. If we then offer the following front engineers with numbers representing preferences: (10, 4, 7, 6, 5, 11, 2, 3), then their accepted engineer sequence would be (6, 6, 4, 4, 4, 4,4, 2, 2). This is non decreasing in preference.
puzzle
On a circular highway there are n petrol stations, unevenly spaced, each containing a different quantity of petrol. It is known that the total amount of petrol from all stations is exactly enough to go around the highway once.
You want to start at a petrol station, take all its fuel, and drive clockwise around the highway once. Each time you reach a petrol station, you will take all its fuel too.1 The only problem is the possibility that you might run out of fuel before reaching the next petrol station!
Prove that there is always at least one starting petrol station to make it around the highway.
Welcome to point out the mistakes and faults!