Basic data structure
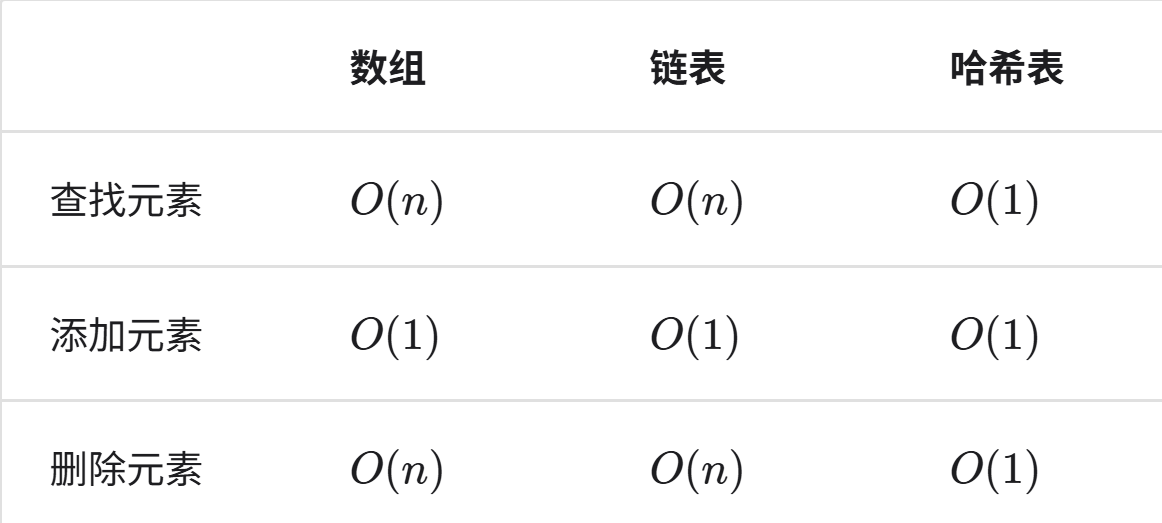
Arrays
- Stores $n$ items, indexed from $1$ to $n$.
- Accessing an element has time complexity $O(1)$; insertion and deletion has time complexity $O(n)$; search has time complexity $O(n)$.
Linked lists
- Stores items in a list where each element has a link to the next element.
- Accessing an element has time complexity $O(n)$; insertion and deletion has time complexity $O(1)$; search has time complexity $O(n)$.
Stacks
- Stores items in LIFO (last-in, first-out) order.
- Accessing the top of the stack has time complexity $O(1)$; insertion and deletion has time complexity $O(1)$ but we can only insert or delete from the top of the stack.
Queues
- Stores items in FIFO (first-in, first-out) order.
- Accessing the front of the queue has time complexity $O(1)$; insertion and deletion has time complexity $O(1)$ but we can only insert or delete from the front of the queue.
Heaps
Stores items in a complete binary tree (Notely
complete binart tree‘s definition, just all full nodes except the lowest layer, and only adjacent lacks on right side 完全二叉树). Minimum heaps ensure that every parent node is $≤$ all of its children nodes. Maximum heaps ensure that every parent node is $≥$ all of its children nodes.Searching for the min/max has time complexity $O(1)$; insertion has time complexity $O(log n)$; deleting the min/max has time complexity $O(log n)$.
We know for a perfect, how to infer its depth by the number of nodes: $H = log_2(N+1)$. Heapify up or down is mainly according to its depth, hence eventually the insertion and deleting for a heap (complete binary tree) is $O(log n)$.
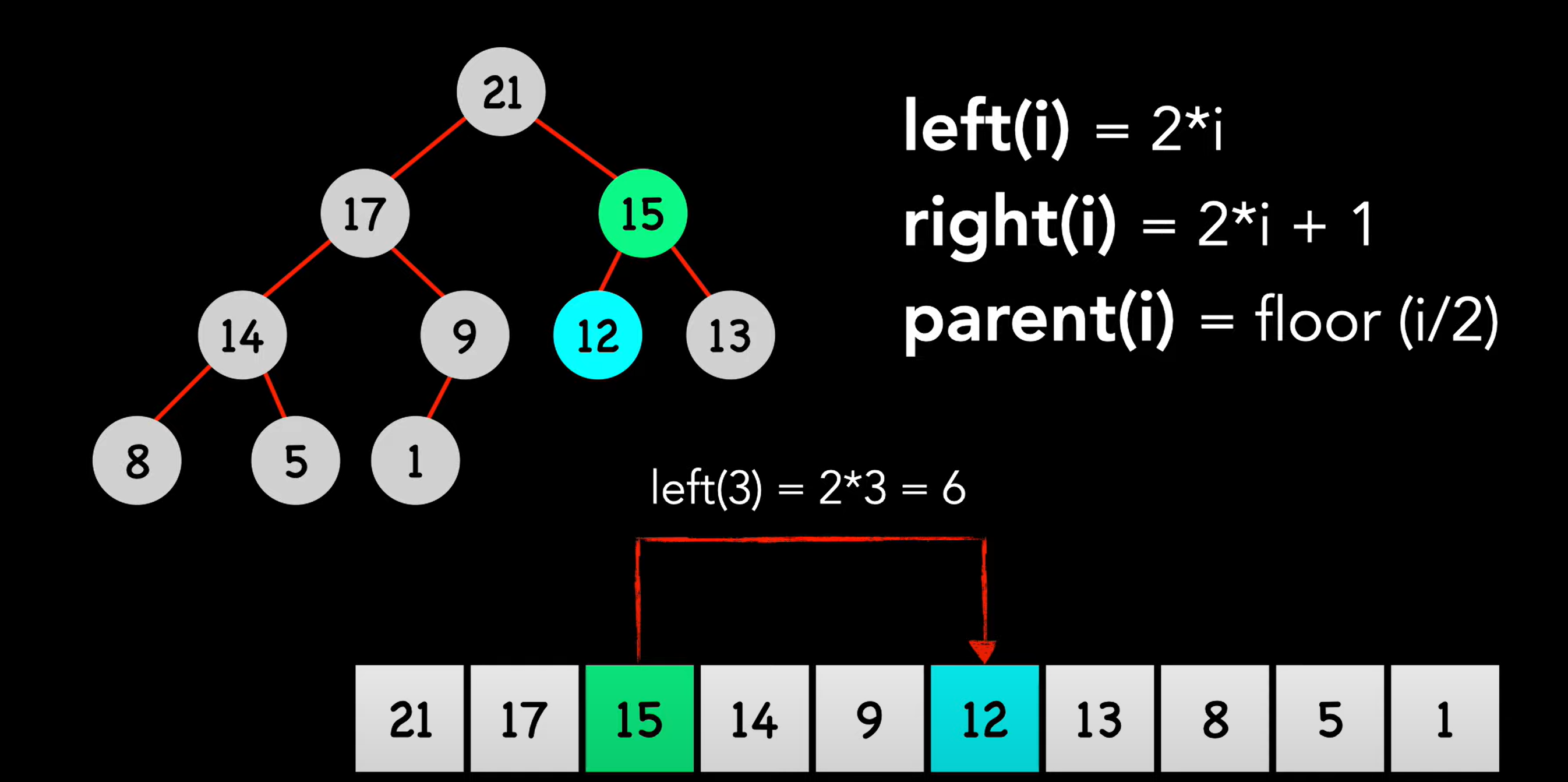
When you want to populate a number, please refer to visually observe heap. The inserted number will always enter at the position of complete tree the lowest leftest position, then follow which type of the heap (Max heap or Min heap), adjust its position on the chain.
heap features
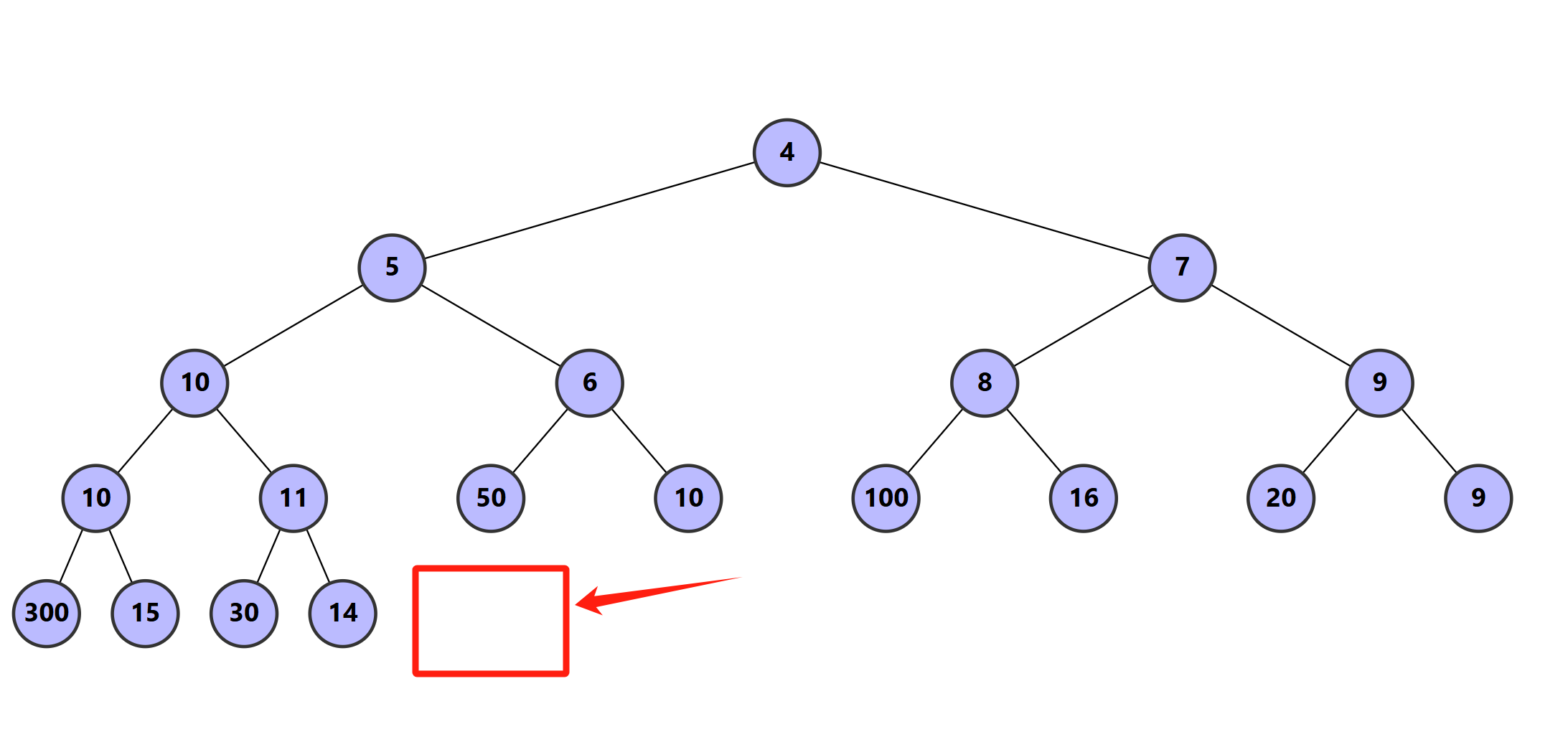
For example, if I want to insert a new 22, at first it will be inserted here.
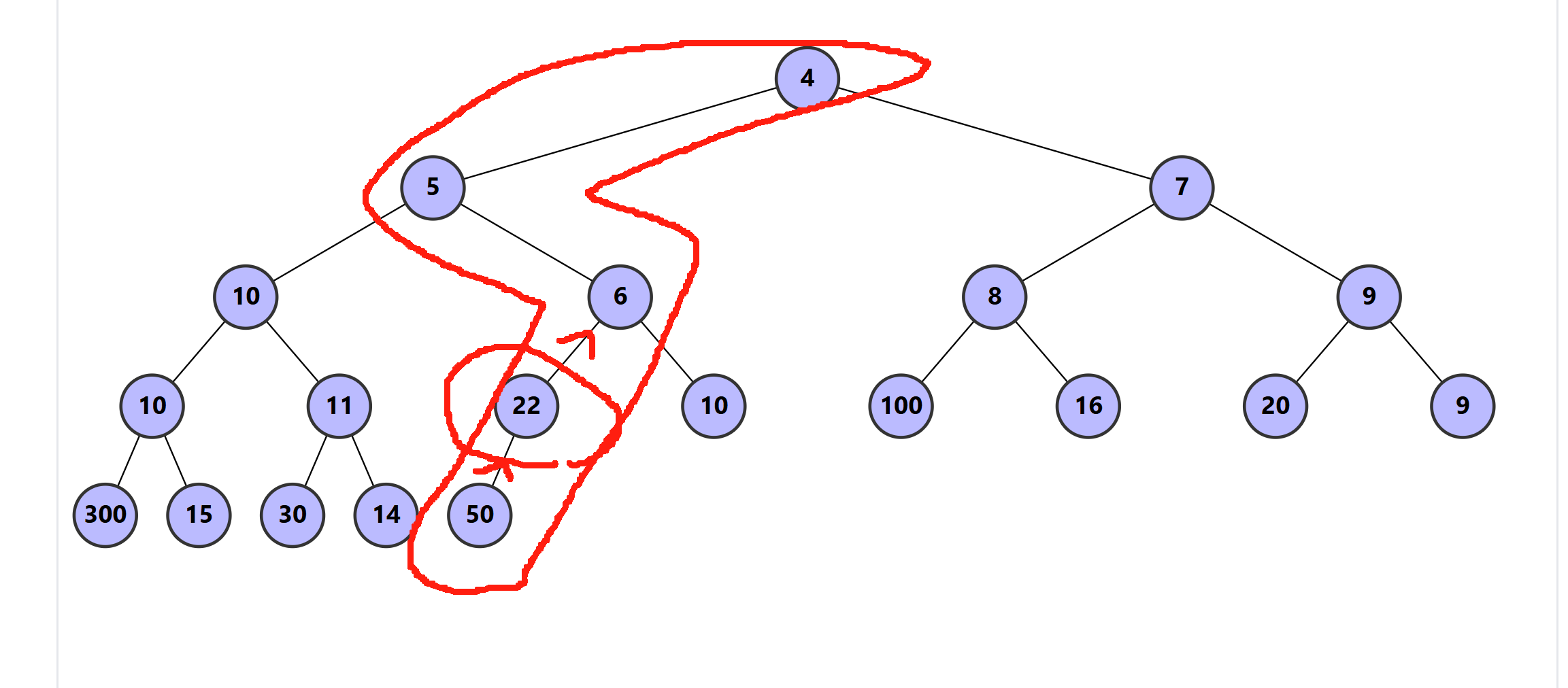
Then followed by the chain, the new number 22 would be adjusted to the position, which is greater than its child and smaller then its parent (heapify-up or heapify-down).
Full Binary Tree
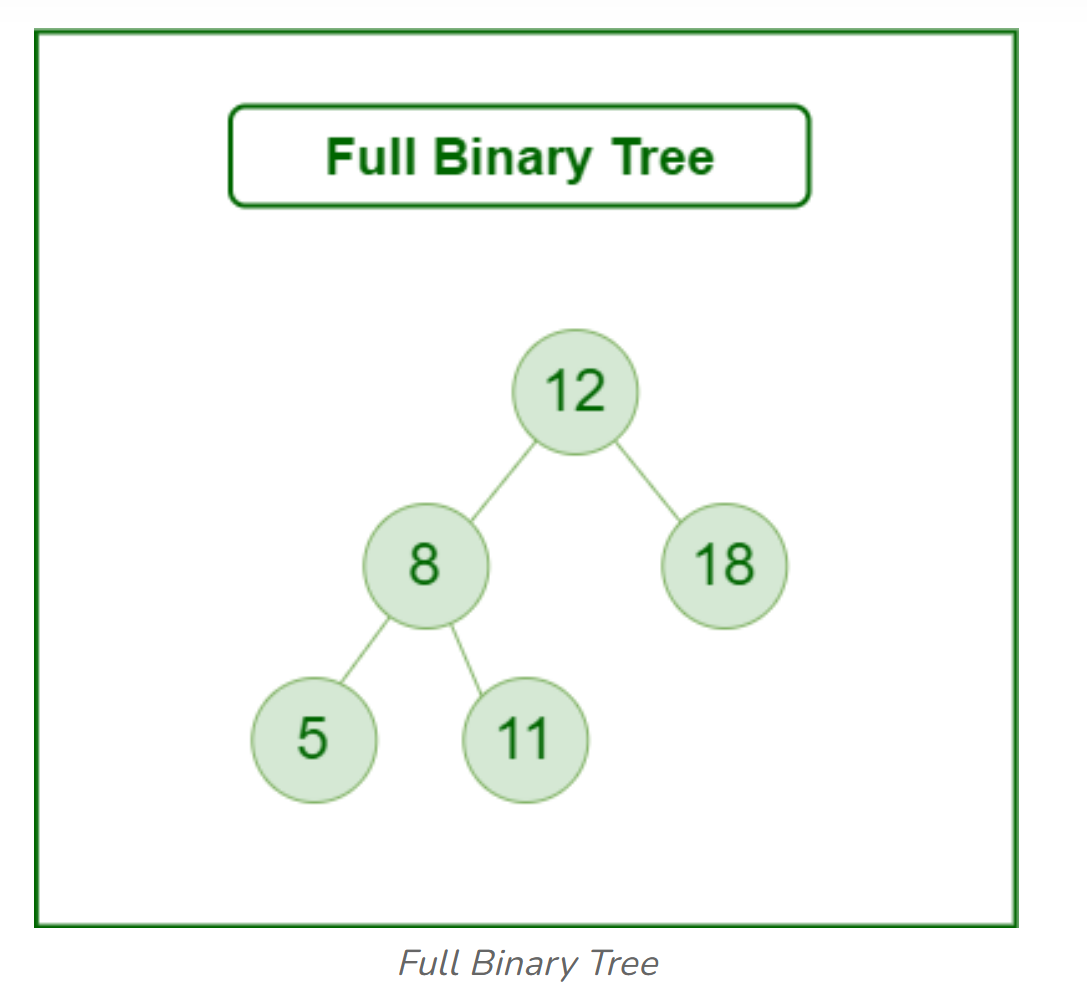
Every has either two or zero children.
Perfect Binary Tree
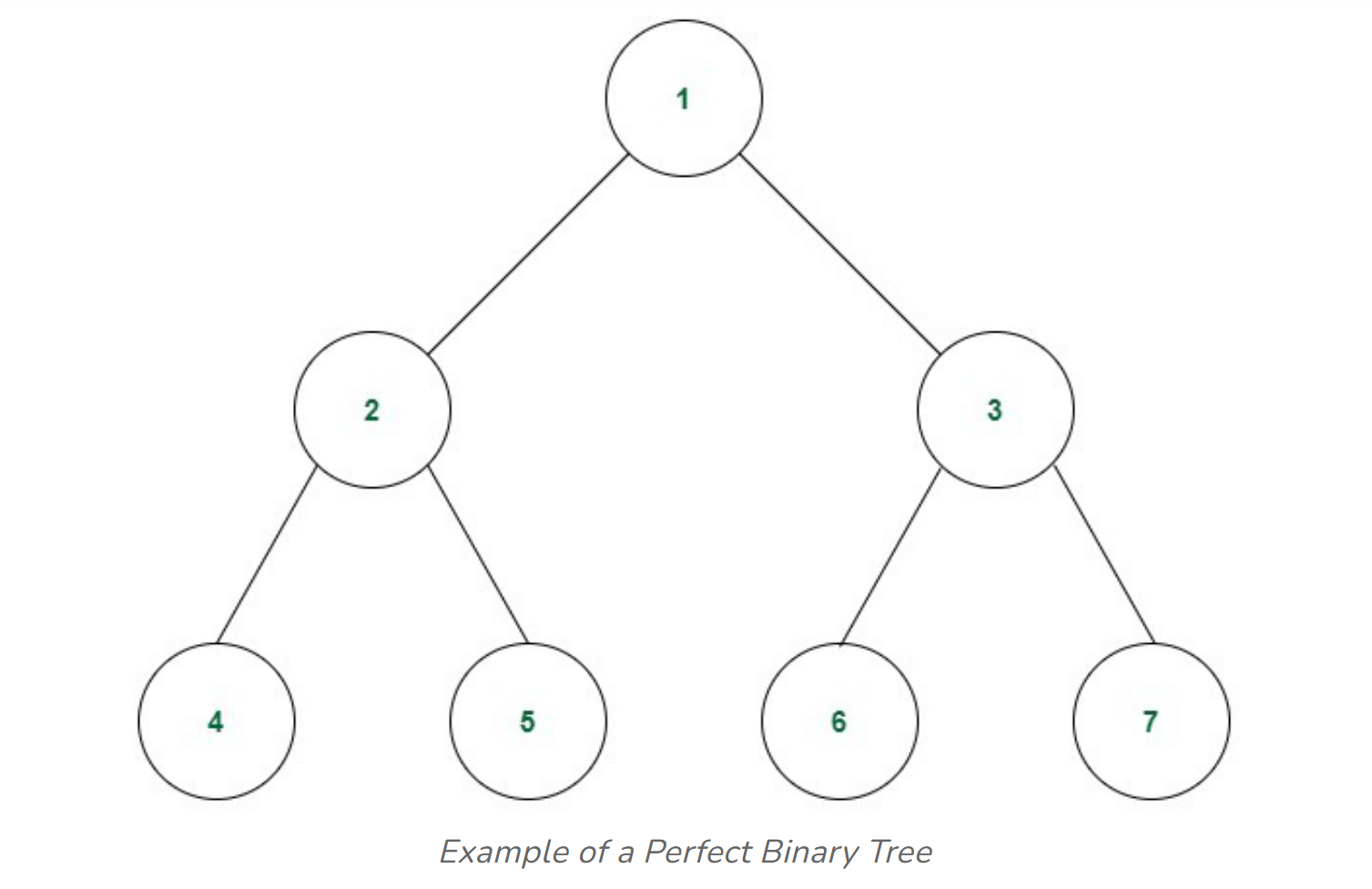
A tree has $k$ layers, and $2^k - 1$ nodes.
A tree with only the root node is also a perfect binary tree.
Assume depth is H
Nodes: $2^H-1$
leaves: $2^{H-1}$
$i$ layer nodes: $2^{i-1}$
infer depth by nodes: $H = log_2(N+1)$
Complete Binary Tree
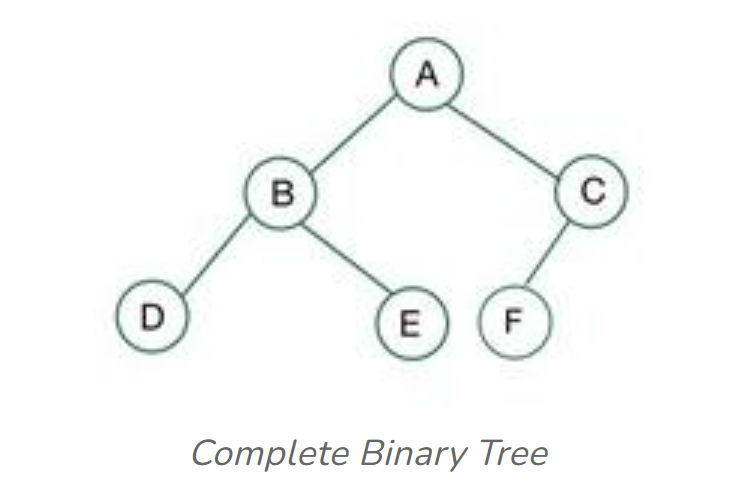
All internal nodes have 2 children, and all leaves are on the same layer.
time complexity
- Searching for the min/max has time complexity $O(1)$
Obviously, a Max Heap’s root is the Maxmium, and a Min Heap’s root is the Minium. Just find the root node, hence it’s $O(1)$
- insertion has time complexity $O(logn)$; deleting the min/max has time complexity $O(log n)$.
reference
Hash tables
- Stores values indexed by keys. A hash function maps keys to indices in a fixed-size table.
- Worst case. Searching for an element given the key has time complexity $O(n)$; insertion and deletion has time complexity $O(n)$.
- Expected case. Searching for an element given the key has time complexity $O(1)$; insertion and deletion has time complexity $O(1)$.
Welcome to point out the mistakes and faults!