- 2n number, the largest number
- 2^n number, the two largest numbers
- two sum
- three sum
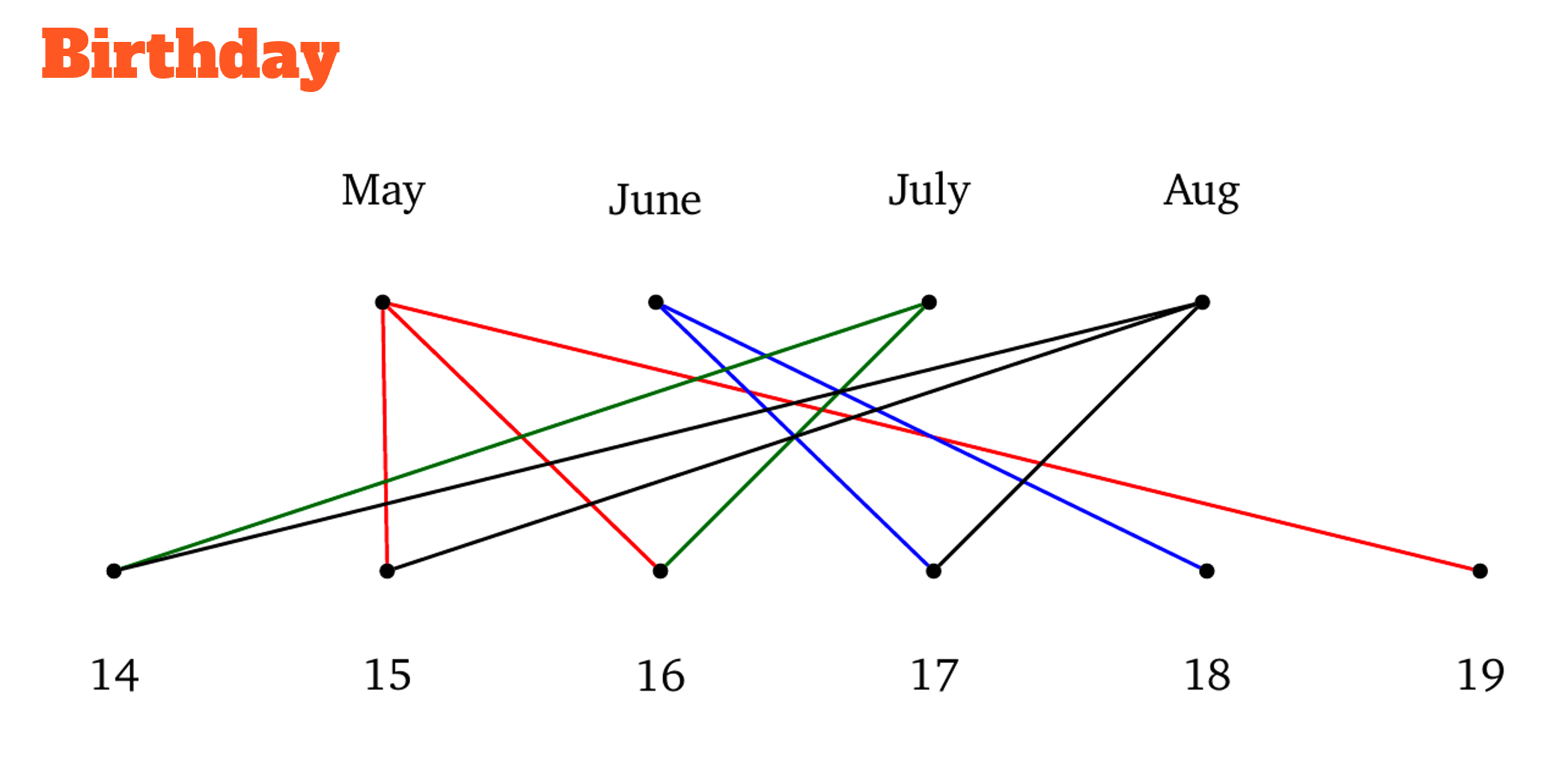
- shortest path
- Birthday in a list

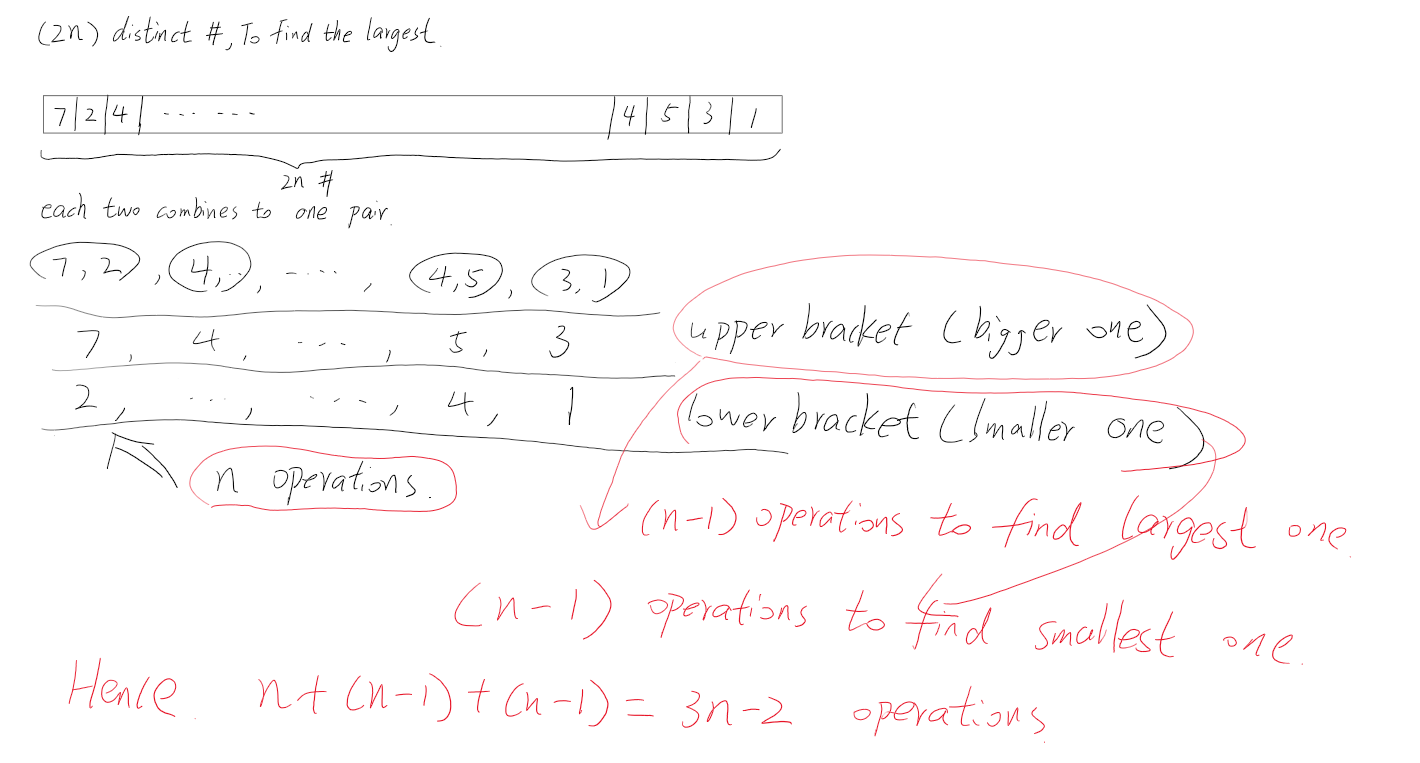
2n number, the largest number
(a) Suppose that you have an array of $2n$ distinct integers. How can you find the smallest and largest integers using at most $3n−2$ comparisons?
Note. Naively finding the smallest and largest integers will take $(2n−1)+(2n − 2)=4n−3$ comparisons, which is too many.Try and eliminate some redundant comparisons.
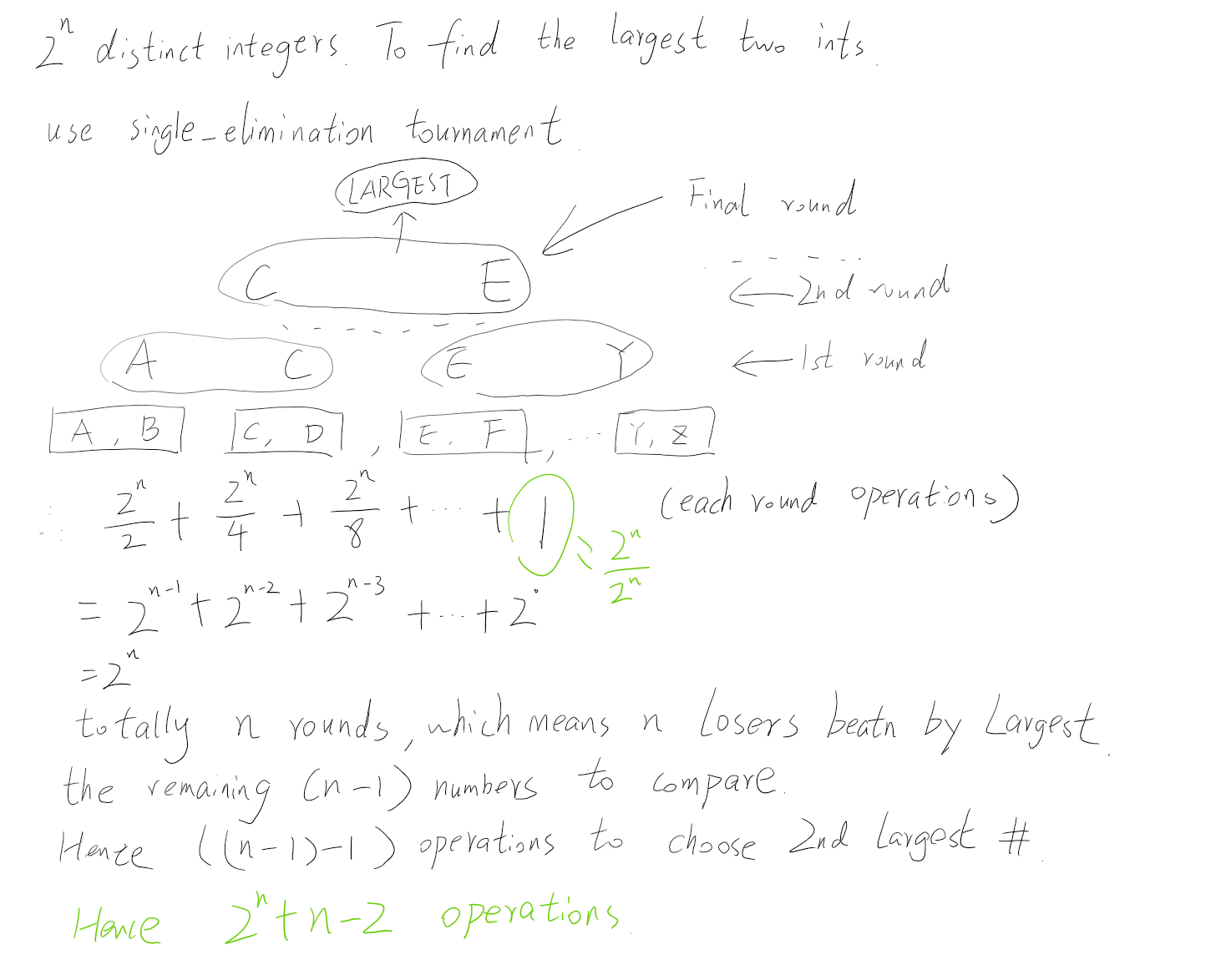
2^n number, the two largest numbers
(b) Now, suppose you have an array of $2^n$ distinct integers. How can you find the largest two integers using at most $2^n+n−2$ comparisons?
Hint. Do something similar with a different data structure.
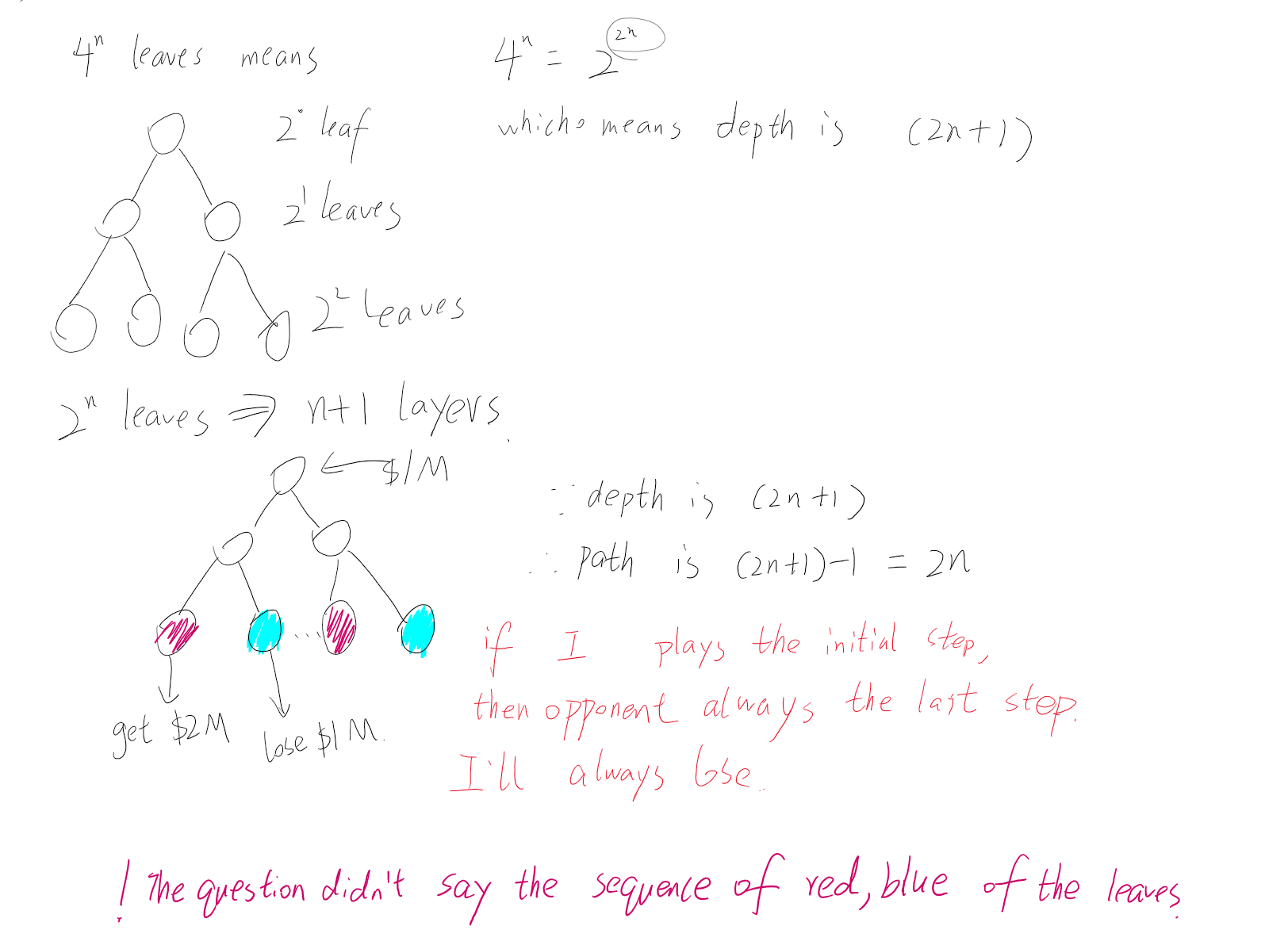
You are handed a complete binary tree with $4^n$ leaves, each leaf coloured either blue or red. You play a game with your friend on the tree. To play the game, you and your friend place down $1 M on the root of the tree. You then take it in turns to move the money down the tree, to one of its children. The game ends when the money lands at one of the leaf vertices.
You win $2M if the coin lands at a leaf vertex coloured red, and lose $1 M if the coin lands at a leaf vertex coloured blue. You make the initial move so that your opponent makes the final move. Your task is to decide whether to play the game or not.

Answer
1. sequence of leaves are random red or blue
Normally, if the sequence of leaves are random red or blue, my friend always take the last step to the two children. Hence it’s possible that he is always intended to choose the blue.
2. if two-two red and blue leaves
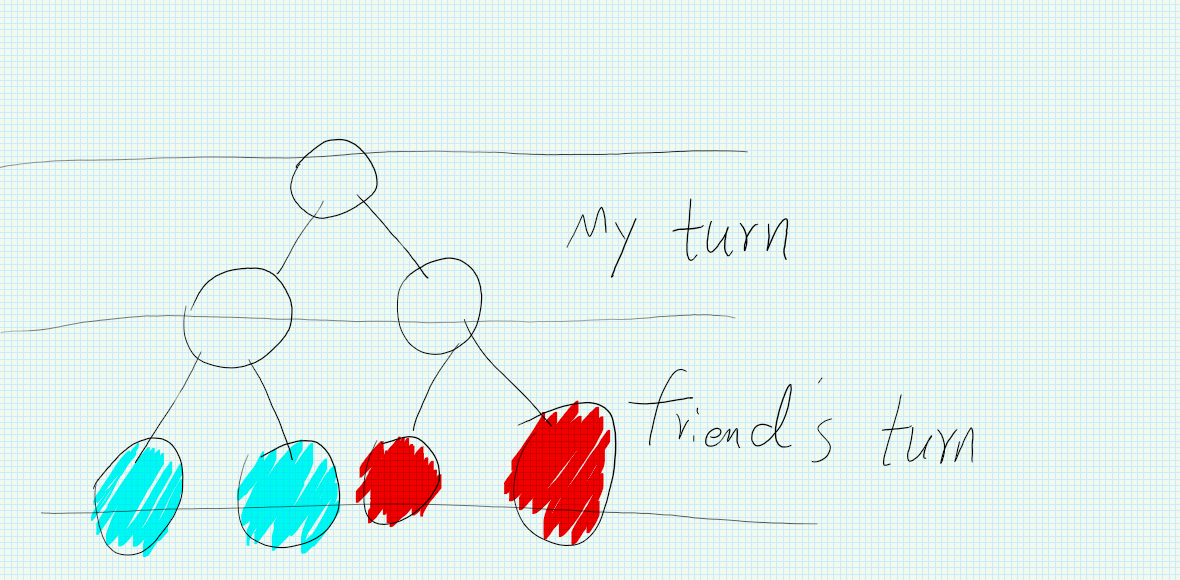
Just like this, if I could control the penultimate turn, I always control the flow into the node with two red leaves.
Then I always win!
two sum

three sum





The minimum time complexity is $O(n^2)$
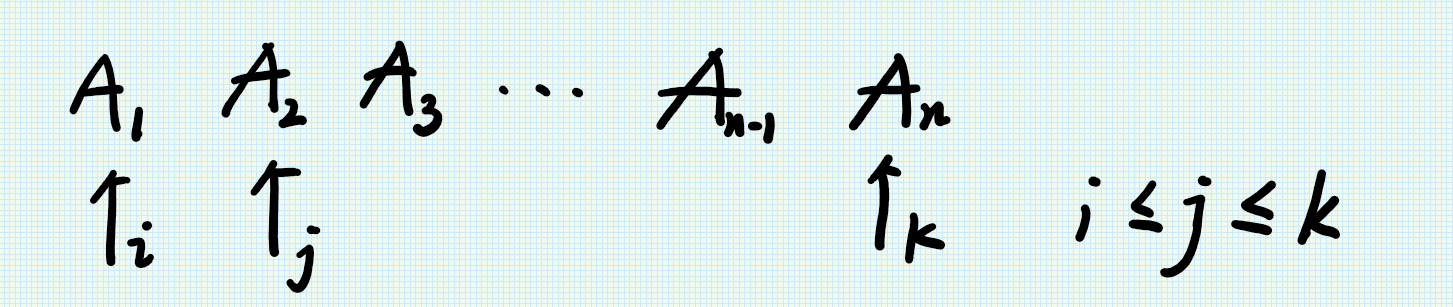
shortest path

Birthday in a list


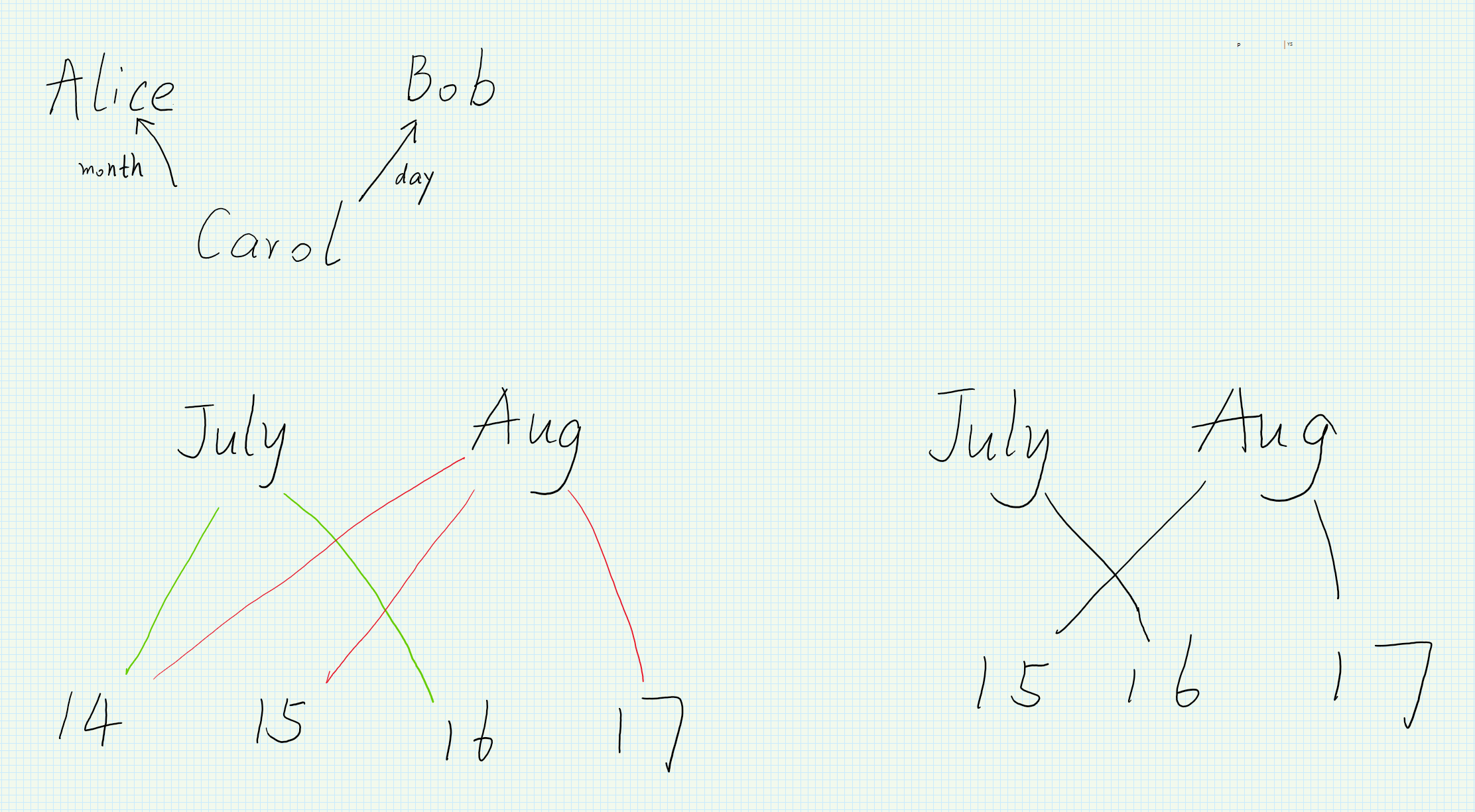
Welcome to point out the mistakes and faults!