- problem of 27 coins, within a counterfeit
- Binary search
- Decision problems and optimisation problems
- Merge sort
- Example:Counting The Number Of inversions
- Introductory Examples
1.1 Coin puzzle
1.2 Binary search
1.3 Merge sort
1.4 Quick sort
1.5 Divide and Conquer paradigm - Recurrences
2.1 Framework
2.2 Master Theorem - Integer Multiplication
3.1 Applying D&C to multiplication of large integers
3.2 The Karatsuba trick - Convolutions
4.1 Polynomials
4.2 The Fast Fourier Transform - Puzzle
problem of 27 coins, within a counterfeit
We are given 27 coins of the same denomination; we know that one of them is counterfeit and that it is lighter than the others. Find the counterfeit coin by weighing coins on a pan balance only three times.
Hint
You can reduce the search space by a third in one weighing!
Solution

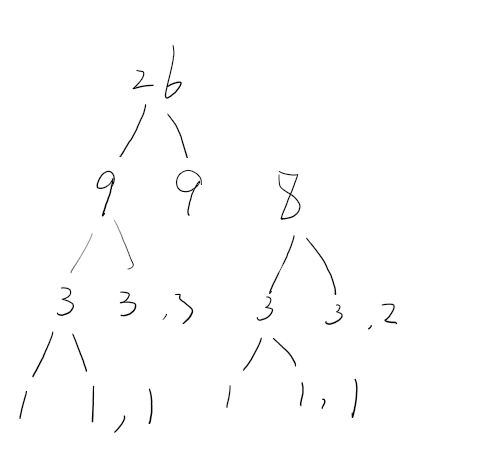
This method is called “divide-and-conquer”.
We have already seen some prototypical “serious” algorithms designed using this method: binary search, merge sort and quicksort.
We’ll now review these algorithms from a divide-and-conquer perspective, and adapt them to solve problems.
Binary search
Steps:
- Divide: Test the midpoint of the search range ($Θ(1)$)
- Conquer: Search one side of the midpoint recursively
- Combine: Pass the answer up the recursion tree (Θ(1))
Recursion is $log_2 n$ levels deep, with a total of $Θ(1)$ time spent in each level.
Time complexity is $Θ(logn)$.
Binary search extensions
Given an array A, sorted in non-decreasing order, and an integer x.
Lower bound: find the smallest index i such that A[i] ≥ x.
Upper bound: find the largest index i such that A[i] ≤ x.
Equal range: find the range of indices $ℓ..r$ such that $A[ℓ] = … = A[r] = x$.
Decision problems and optimisation problems
Decision problems
Questions of the form: “Given some input, is there an x which . . . ”
Answer is “Yes” or “No”.
Optimisation problems
Questions of the form: “What is the smallest/largest x for which …”
Answer is an object, e.g., a set or a number.
An optimisation problem is typically harder than the corresponding decision problem.
But we can sometimes use decision problems to help us solve optimisation problems.
Definition
Recall that the median of an array is the middle value in sorted order.
For example, the median of [1,2,2,4,5] is 2.
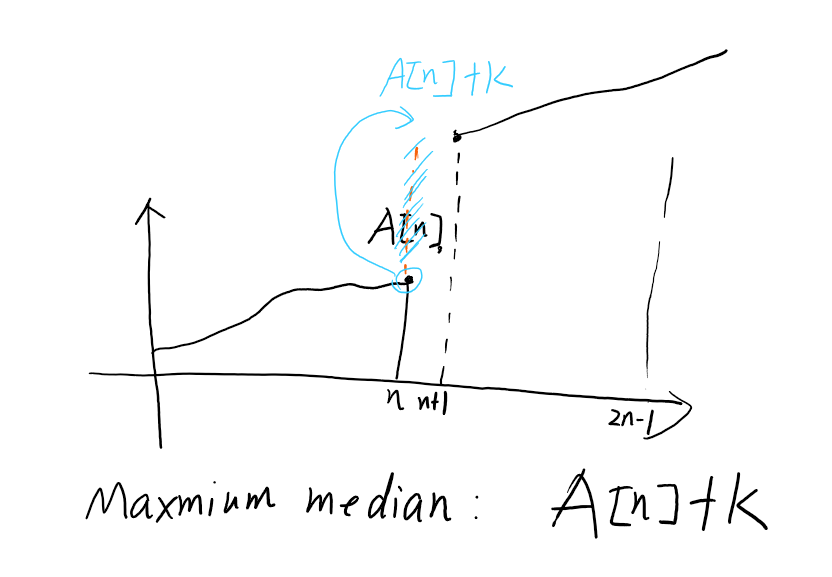
Problem: Example optimisation problem: Maximum Median
Ling has an array A consisting of 2n-1 integers, sorted from smallest to largest. Note that the median is initially A[n].
She wants her numbers to grow big and strong, so for each of the following $k$ days she adds 1 to one of her numbers.
At the end of the $k$ days, what is the largest possible median that her array can have?
Example
If the starting array is [1,2,2,4,5] and k=3, the maximum median is 4, achieved by adding 1 to the third number on the first two days and to any number on the last day.
Using all three increases on the third number does not make the median value 5.
Related problem
Given positive integers $t$ and $k$. Ling wants to know whether she can make the median of her numbers at least the target value $t$ (by adding $1$ to one of her numbers each day for $k$ days).
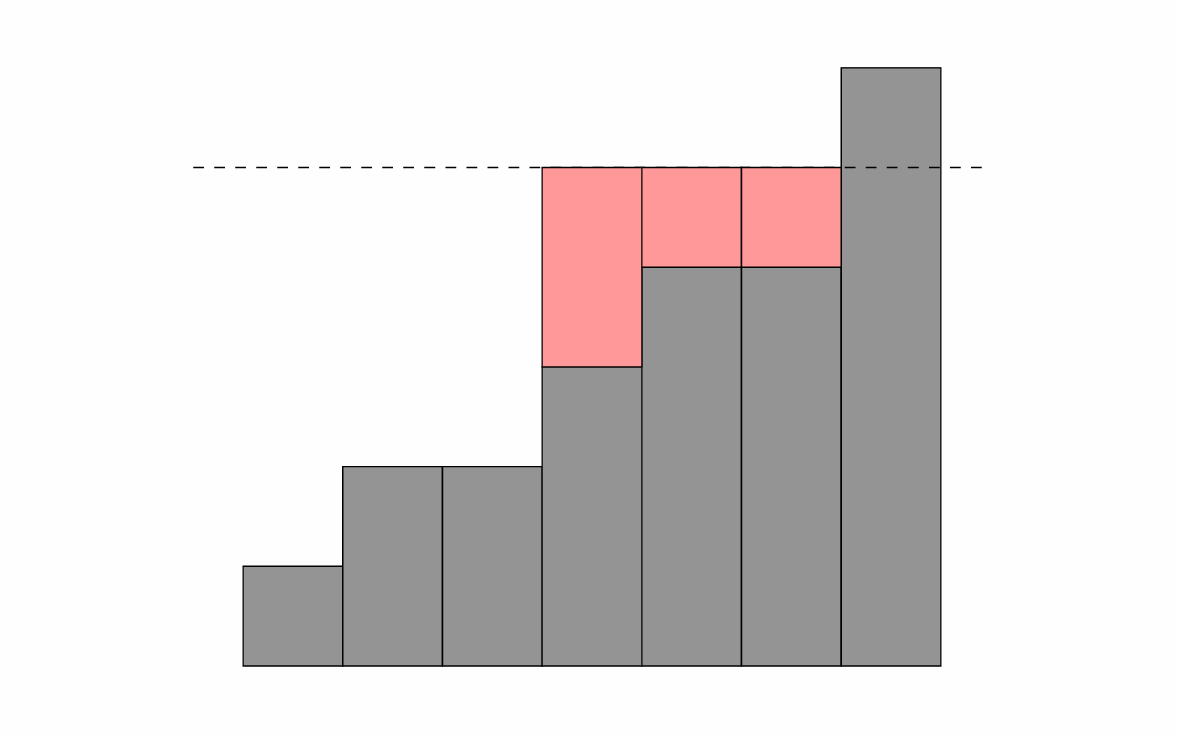
How do we get the median to at least t?
- Increase the middle value A[n] and everything after it to $t$;
nothing to do for any values that are $≥t$ already.
Why might we fail?
- $t$ could be too big (relative to $k$). I.e. if $k$ is too small then we could run out of days.
- Unused days are fine (so long as our array has at least 3 entries).
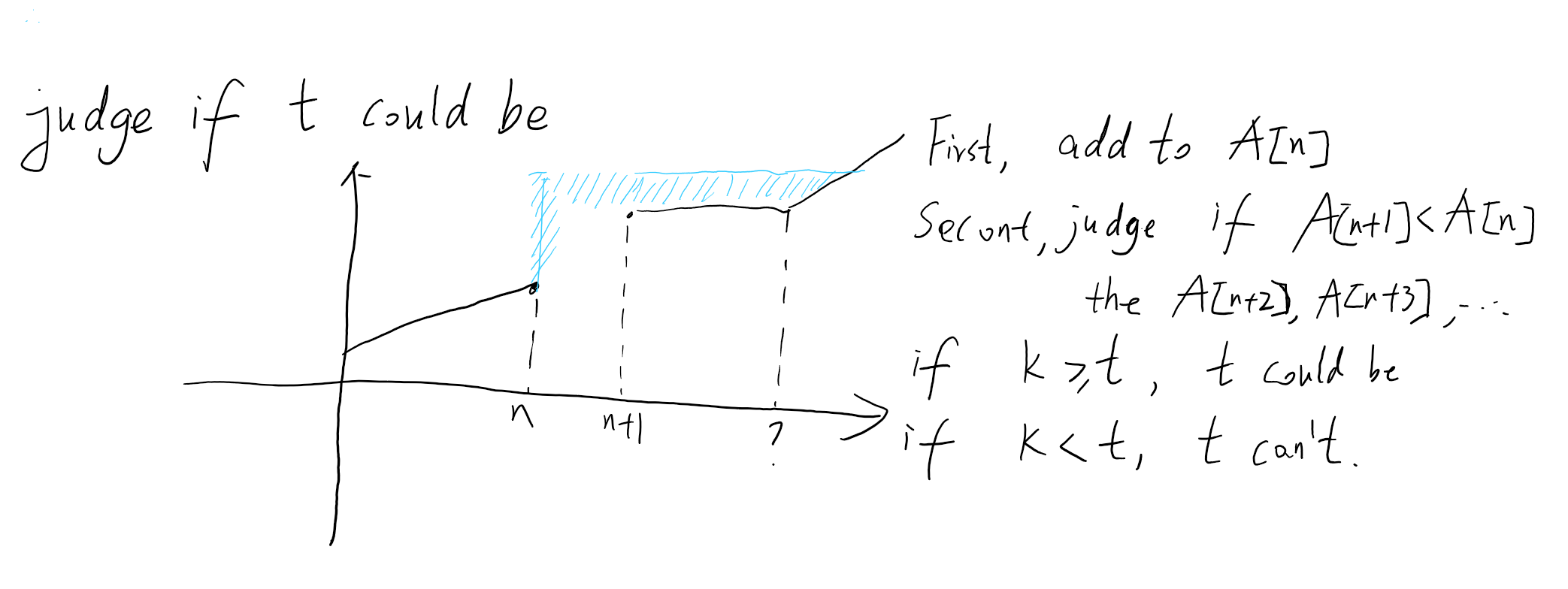
Algorithm (for related problem)
If this value is $≤k$, report yes; otherwise report no.
This algorithm clearly runs in $O(n)$ in the worst case.
Merge sort
Steps:
Divide: Split the array into two equal parts $(Θ(1))$
Conquer: Sort each part recursively
Combine: Merge the two sorted subarrays $(Θ(n))$
Recursion is $log_2 n$ levels deep, with a total of $Θ(n)$ time spent in each level.
Time complexity is $Θ(nlogn)$.
Example:Counting The Number Of inversions
Welcome to point out the mistakes and faults!